How to Explain the Higgs Mechanism

Greetings from chilly Toronto, where I’m briefly in town to participate in a public event about the Higgs boson tonight. Should be a good time, especially because it’s not just me giving a talk; I will spend 20 minutes explaining the theoretical motivation behind the Higgs, after which experimentalists Pierre Savard and William Trischuk will talk about the actual experiments.

Which raises the question: how does one explain the theoretical motivation behind the Higgs, given a small number of minutes and a motivated-but-nonexpert audience? It’s something I should have figured out by now, having written a book and all. But I’ve been fishing around, and I think I’ve finally settled on a favorite approach to doing it.

A couple of preliminary notes. I don’t think there is a good explanation of the Higgs boson at the sound bite level, say 15 seconds or less. That’s because you need to explain two distinct things: first, that there is a Higgs field filling space that interacts with the particles moving through it and giving some of them mass; and second, that the Higgs boson is the particle we observe when we interact with a vibration in that field. Both of these ideas are part of quantum field theory, which we generally don’t try to explain in physics popularizations, so it’s more than a few seconds of work to get them across. But I don’t think there is a shortcut: if you want to explain the Higgs at all, you have to explain the Higgs field.

With that in mind, the biggest stumbling block to providing a convincing popular-level motivation for the Higgs field is that we immediately leap to the idea that the role of the Higgs is to “give particles mass,” where by “particles” we really mean “quarks, charged leptons, and the W & Z bosons.” This raises a couple of problems. First, why do we need some mechanism to give particles mass? Why can’t they just have mass? Of course some particles can just have mass — like the Higgs itself. So you’re starting off by moving backwards, bringing up the need to explain why different symmetries apparently prevent particles from having mass, which is actually harder to explain than the Higgs mechanism. And second, most of the mass in real objects comes from QCD, not from the Higgs mechanism at all, so you are almost inevitably giving people the wrong idea. You see why it’s a tricky situation.

Fortunately, we have an alternative: the actual historical development of the subject. Back in the early 1960’s when the Higgs mechanism was being proposed (by Anderson, Englert, Brout, Higgs, Hagen, Guralnik, and Kibble), they weren’t trying to give mass to fermions. They were trying to explain how nuclear forces, which manifestly only stretch over a very short distance, could possibly be described in a way similar to gravity and electromagnetism (i.e. by Yang-Mills theories), which manifestly stretch over long distances. Sure, both gravity and E&M fade away as you move farther from a source, but they do so slowly (the inverse square law, in particular), which is why they are relatively easy to observe in the everyday world. If the nuclear forces are simply generalizations of E&M, as Yang and Mills suggested, why don’t they stretch over large distances?

Here is the analogy I’d like to suggest. Think of someone holding a lantern on a dark night. As that person moves farther away from you, the light you receive from the lantern grows dimmer; indeed, it follows exactly an inverse-square law. That makes sense, when you simply think of the rays of light emerging from the lantern in three dimensions. Long-range forces are like that, with “rays of light” replaced by “lines of force.”

So what you want to account for is how a lantern could seem quite bright when it was nearby, but quickly fade to almost nothing as it moves just a short distance away. That is, how a force could be noticeable at short range, but cut off dramatically at longer distances.

Well, there are a couple of ways to do it, and nature takes advantage of both of them. One way is to simply put some kind of shield or shutter around the lantern, keeping the light trapped inside. If you were inside the shutter, the lantern would look quite bright; but as soon as you step outside, you can barely see it if at all.

We call that phenomenon confinement. It’s what the strong nuclear force does. The force-carrying bosons (gluons) are still massless, but they interact with each other so strongly that they can’t leak outside. If you were inside a nucleus, the strong force would seem quite strong; outside, it’s barely noticeable. (To make the analogy exact you would have to make the shutter itself out of light, but analogies are rarely exact.)

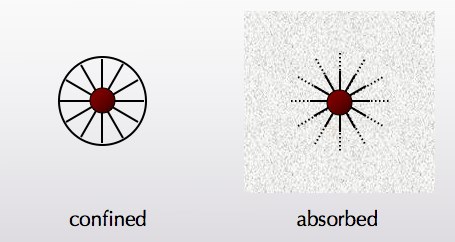
The other possibility is that the lantern is unshuttered, but that the air is full of fog. (Something truly absorbing rather than scattering would make for a more exact analogy, so maybe smog would be better than fog.) Then the light from the lantern can’t propagate very far because it is absorbed by the medium filling the space between it and you.

That’s the Higgs mechanism, and it’s what makes the weak nuclear force short-range. There is a field filling space, which absorbs the lines of weak force. It’s a pretty good analogy to the fog; in both cases, the absorbing material creates an effectively short-range phenomenon. If you were closer to the lantern than the attenuation length in the fog, you would be able to see it with no problem; likewise, if you are closer to a source of the weak force than the mass of the W/Z bosons, it would be very noticeable. This analogy, one hopes, helps get across the need for a field filling space, which is what the Higgs field is all about.

Now of course you should probably try to explain why fog would give mass to something. That’s left as an exercise for the reader.