This year we give thanks for an idea that establishes a direct connection between the concepts of “energy” and “information”: Landauer’s Principle. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, and gauge symmetry.)
Landauer’s Principle states that irreversible loss of information — whether it’s erasing a notebook or swiping a computer disk — is necessarily accompanied by an increase in entropy. Charles Bennett puts it in relatively precise terms:
Any logically irreversible manipulation of information, such as the erasure of a bit or the merging of two computation paths, must be accompanied by a corresponding entropy increase in non-information bearing degrees of freedom of the information processing apparatus or its environment.
The principle captures the broad idea that “information is physical.” More specifically, it establishes a relationship between logically irreversible processes and the generation of heat. If you want to erase a single bit of information in a system at temperature T, says Landauer, you will generate an amount of heat equal to at least
![]()
where k is Boltzmann’s constant.
This all might come across as a blur of buzzwords, so take a moment to appreciate what is going on. “Information” seems like a fairly abstract concept, even in a field like physics where you can’t swing a cat without hitting an abstract concept or two. We record data, take pictures, write things down, all the time — and we forget, or erase, or lose our notebooks all the time, too. Landauer’s Principle says there is a direct connection between these processes and the thermodynamic arrow of time, the increase in entropy throughout the universe. The information we possess is a precious, physical thing, and we are gradually losing it to the heat death of the cosmos under the irresistible pull of the Second Law.
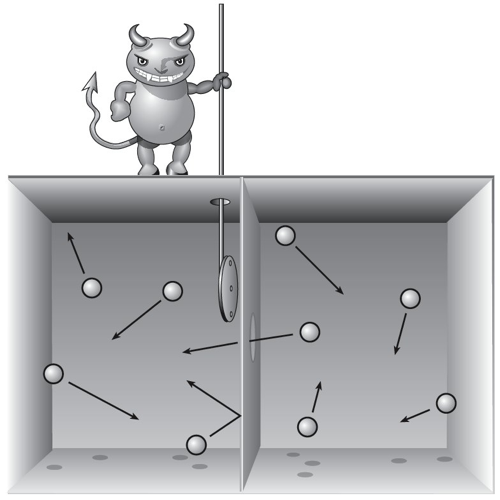
The principle originated in attempts to understand Maxwell’s Demon. You’ll remember the plucky sprite who decreases the entropy of gas in a box by letting all the high-velocity molecules accumulate on one side and all the low-velocity ones on the other. Since Maxwell proposed the Demon, all right-thinking folks agreed that the entropy of the whole universe must somehow be increasing along the way, but it turned out to be really hard to pinpoint just where it was happening.
The answer is not, as many people supposed, in the act of the Demon observing the motion of the molecules; it’s possible to make such observations in a perfectly reversible (entropy-neutral) fashion. But the Demon has to somehow keep track of what its measurements have revealed. And unless it has an infinitely big notebook, it’s going to eventually have to erase some of its records about the outcomes of those measurements — and that’s the truly irreversible process. This was the insight of Rolf Landauer in the 1960’s, which led to his principle.
A 1982 paper by Bennett provides a nice illustration of the principle in action, based on Szilard’s Engine. Short version of the argument: imagine you have a piston with a single molecule in it, rattling back and forth. If you don’t know where it is, you can’t extract any energy from it. But if you measure the position of the molecule, you could quickly stick in a piston on the side where the molecule is not, then let the molecule bump into your piston and extract energy. The amount you get out is (ln 2)kT. You have “extracted work” from a system that was supposed to be at maximum entropy, in apparent violation of the Second Law. But it was important that you started in a “ready state,” not knowing where the molecule was — in a world governed by reversible laws, that’s a crucial step if you want your measurement to correspond reliably to the correct result. So to do this kind of thing repeatedly, you will have to return to that ready state — which means erasing information. That decreases your phase space, and therefore increases entropy, and generates heat. At the end of the day, that information erasure generates just as much entropy as went down when you extracted work; the Second Law is perfectly safe.
The status of Landauer’s Principle is still a bit controversial in some circles — here’s a paper by John Norton setting out the skeptical case. But modern computers are running up against the physical limits on irreversible computation established by the Principle, and experiments seem to be verifying it. Even something as abstract as “information” is ultimately part of the world of physics.
Fair enough Alex, but I take my cue from relativity, wherein matter is made of energy and field energy is a state of space. Energy is fundamental, and at the fundamental level you cannot distinguish it from space. Information is the “pattern”, entropy is the “sameness” relating to available energy, no problem with that. But conservation of energy applies, it’s the one thing you can neither create not destroy. And it’s energy that’s physical, as is matter, as are the coins. However the pattern of the coins isn’t something physical in itself, just as colour isn’t physical because it’s a quale. So the idea that information is in itself physical or fundamental leaves me cold I’m afraid.
I had read Brian Greens latest book that touched a little upon this topic. But, it mentioned that a particle reflected in a box would contain some unknown amount of energy, and in their attempt to solve an equation for the total energy in the box, they only got infinite answers and threw out the theory. It mentioned something about this being due to “quantum jitters”. Then it came up as part of a problem in trying to solve for dark energy, and it was part of a problem from talks with people involving the findings for the cosmological constant.
I would be interested on your thoughts one this, and how you would calculate a particle being reflected in a box over time.
Error, post deleted
Entropy as I see it is an endogenous increase of either mass or energy.
According to quantum mechanics, information can’t be destroyed (General Relativity says it can, but I think most physicists would say that QM “trumps” GR on this – Hawking recently gave up on one of his famous bets on “the black hole information paradox” for example).
Hence according to QM, the concept of erasing information isn’t physically correct.
I might also mention that entropy is generally considered an emergent concept, rather than anything fundamental to the operation of the universe. It occurs because of the expansion of the universe, the way the components of the universe are arranged, and so on. The laws of physics are time-symmetric with only one known violation, which is generally thought to be unimportant in most physical processes, especially ones which are involved in the entropy gradient (although of course this may turn out to be wrong – perhaps neutral kaon decay had a significant impact in the first few seconds after the Big Bang).
@LizR, this is my sense of it too, but this deepens the puzzle as far the ontological status of information goes. What you’re saying is that information as a fundamental quantity cannot be lost. Landauer’s principle relates information loss to entropy increase, a relationship between something fundamental and something emergent. The way we get an arrow of time (to “emerge”) from time-symmetric fundamental laws is by initial conditions, a past that is in a lower entropy state. How do we get heat generation from “fundamental” information loss? Or is information loss always only “emergent” in some sense?
Does Landauer’s analysis allow for temporary reversals of entropy in isolated systems, in between periodic erasures of the demon’s memory? Of course in statistical mechanics you can always have random fluctuations that lower the entropy in an isolated system, but I’m talking about a scenario where the odds are strongly in favor of an entropy decrease over a given span of time, not just a statistical fluke. This would seem to violate the fluctuation theorem but perhaps there are restrictions on the types of systems that theorem is meant to apply to.
The issue with “conservation of information” in QM is resolved as follows. To define a thermodynamic system rigorously, you need to do a coarse graining over microscopic degrees of freedom, leaving you with the parameters that you use to describe the system. Entropy is (expressed in the right units) precisely the amount of information that you lose in this coarse graining process.
Then given a thermodynamic state, the entropy gives you thelogarithm of the number of microstates that will be mapped to the same macrostate. Hoewever, while all these microstates have the same macroscopic thermodynamic properties, that does not mean that the system can really be in any one of these states. E.g. consider a gas undergoing free expansion in a perfectly isolated box that will even prevent decoherence so that it evolves in a unitary way. Clearly, while the entropy increases in the usual way, the number of states the system really can be in must be identical to what it was before the gas expanded. These states will under time reversal evolve back to the unexpanded state. But macroscopically, these states are indistinguishable from “fictitious” states that the gas certainly cannot really be in, the vast majority of these states don’t evolve back under time reversal.
/We record data, take pictures, write things down, all the time — and we forget, or erase, or lose our notebooks all the time, too. Landauer’s Principle says there is a direct connection between these processes and the thermodynamic arrow of time, the increase in entropy throughout the universe./
“Time dilation” is a physical reality because, of the speed at which our body ages and the speed of light is constant – so “rest mass” is a relative order.
Time is merely a mathematical quantity (numerical order) of material change. In physical world, time is exclusively a mathematical quantity.
In 1926 Max Planck wrote an important paper on the basics of thermodynamics. He indicated the principle…
“The internal energy of a closed system is increased by an isochoric adiabatic process.”
This proves the expansion of space ? If mass = energy (radioactive), if Speed of light is constant and the universe is expanding, so what is happening to time?
My first encounter with Sean’s blog took place a few years ago, with a post called “The Arrow of Time in Scientific American,” when the blog was still in “Cosmic Variance.” I got there by googling Sean’s name after the said SciAm article got me intrigued. And the reason for my special interest was IMAP (=Information & Meaning Are Physics.)
IMAP is a private, independent, research project of mine, in which I have engaged myself in recent years, unfortunately on and off. It is an interdisciplinary project, lying at the interface of physics, information theory, psychology and philosophy. IMAP aims high: it’s about generalizing the concept of information and, in particular, of the MEANING carried by it, accross all of reality—from the dumbest piece of rock to man-made IT devices to the smartest human brain.
In IMAP, the term “information” (not the quantity of it) is not restricted to signals meaningful to minds, and information meaningful to a mind is not in a separate category from random signals transmitted over a communication channel or from microstates of a volume of gas. All signals may be attributed with meanings pertinent to the systems they interact with, and no system is considered transcendental on grounds of its presumed ability to “understand” the meaning of a signal (in contrast to just acting on it.)
My work on IMAP involved intensive reading and thinking about entropy—Clausius’, Boltzmann’s and Shannon’s—and so I found myself the first time in Sean’s blog (in which I deposited a comment concerning the unhelpfulness of characterizing entropy as a measure of disorder.) Landauer’s Principle and Bennett’s and Zurek’s papers were naturally part of that study, as they are instrumental for the unification of the above three entropy concepts.
I idly returned to visit Sean’s blog, in its present home, only recently, while organizing my Favorites folder. And I stayed on. What a coincidence: I didn’t have to wait long before this thanksgiving post appeared, to which subject I am particularly connected. It surely seems a blog for me, and I must have been lucky chancing upon it. So, here’s some thanksgiving to you, Sean.
“Short version of the argument: imagine you have a “piston” with a single molecule in it, rattling back and forth.”
Shouldn’t that be “cylinder”? Pistons operate inside cylinders.