Usually, technical advances in mathematical physics don’t generate a lot of news buzz. But last year a story in Quanta proved to be an exception. It relayed the news of an intriguing new way to think about quantum field theory — a mysterious mathematical object called the Amplituhedron, which gives a novel perspective on how we think about the interactions of quantum fields.
This is cutting-edge stuff at the forefront of modern physics, and it’s not an easy subject to grasp. Natalie Wolchover’s explanation in Quanta is a great starting point, but there’s still a big gap between a popular account and the research paper, in this case by Nima Arkani-Hamed and Jaroslav Trnka. Fortunately, Jaroslav is now a postdoc here at Caltech, and was willing to fill us in on a bit more of the details.
“Halfway between a popular account and a research paper” can still be pretty forbidding for the non-experts, but hopefully this guest blog post will convey some of the techniques used and the reasons why physicists are so excited by these (still very tentative) advances. For a very basic overview of Feynman diagrams in quantum field theory, see my post on effective field theory.
I would like to thank Sean to give me an opportunity to write about my work on his blog. I am happy to do it, as the new picture for scattering amplitudes I have been looking for in last few years just recently crystalized in the object we called Amplituhedron, emphasizing its connection to both scattering amplitudes and the generalization of polyhedra. To remind you, “amplitudes” in quantum field theory are functions that we square to get probabilities in scattering experiments, for example that two particles will scatter and convert into two other particles.
Despite the fact that I will talk about some specific statements for scattering amplitudes in a particular gauge theory, let me first mention the big picture motivation for doing this. Our main theoretical tool in describing the microscopic world is Quantum Field Theory (QFT), developed more than 60 years ago in the hands of Dirac, Feynman, Dyson and others. It unifies quantum mechanics and special theory of relativity in a consistent way and it has been proven to be an extremely successful theory in countless number of cases. However, over the past 25 years there has been an increasing evidence that the standard definition of QFT using Lagrangians and Feynman diagrams does not exhibit simplicity and sometimes even hidden symmetries of the final result. This has been most dramatically seen in calculation of scattering amplitudes, which are basic objects directly related to probabilities in scattering experiments. For a very nice history of the field look at the blog post by Lance Dixon who recently won together with Zvi Bern and David Kosower the Sakurai prize. There are also two nice popular articles by Natalie Wolchover – on the Amplituhedron and also the progress of understanding amplitudes in quantum gravity.
The Lagrangian formulation of QFT builds on two pillars: locality and unitarity, which means that the particle interactions are point-like and sum of the probabilities in scattering experiments must be equal to one. The underlying motivation of my work is a very ambitious attempt to reformulate QFT using a different set of principles and see locality and unitarity emerge as derived properties. Obviously I am not going to solve this problem but rather concentrate on a much simpler problem whose solution might have some features that can be eventually generalized. In particular, I will focus on on-shell (“real” as opposed to “virtual”) scattering amplitudes of massless particles in a “supersymmetric cousin” of Quantum Chromodynamics (theory which describes strong interactions) called N=4 Super Yang-Mills theory (in planar limit). It is a very special theory sometimes referred as “Simplest Quantum Field Theory” because of its enormous amount of symmetry. If there is any chance to pursue our project further we need to do the reformulation for this case first.
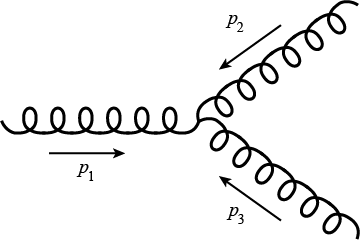
Feynman diagrams give us rules for how to calculate an amplitude for any given scattering process, and these rules are very simple: draw all diagrams built from vertices given by the Lagrangian and evaluate them using certain rules. This gives a function M of external momenta and helicities (which is spin for massless particles). The Feynman diagram expansion is perturbative, and the leading order piece is always captured by tree graphs (no loops). Then we call M a tree amplitude, which is a rational function of external momenta and helicities. In particular, this function only depends on scalar products of momenta and polarization vectors. The simplest example is the scattering of three gluons,
represented by a single Feynman diagram.
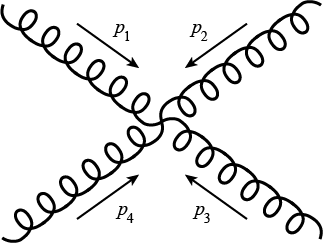
Amplitudes for more than three particles are sums of Feynman diagrams which have internal lines represented by factors P^2 (where P is the sum of momenta) in the denominator. For example, one part of the amplitude for four gluons (2 gluons scatter and produce another 2 gluons) is
Higher order corrections are represented by diagrams with loops which contain unfixed momenta – called loop momenta – we need to integrate over, and the final result is represented by more complicated functions – polylogarithms and their generalizations. The set of functions we get after loop integrations are not known in general (even for lower loop cases). However, there exists a simpler but still meaningful function for loop amplitudes – the integrand, given by a sum of all Feynman diagrams before integration. This is a rational function of helicities and momenta (both external and loop momenta) and it has many nice properties which are similar to tree amplitudes. Tree amplitudes and Integrand of loop amplitudes are objects of our interest and I will call them just “amplitudes” in the rest of the text.
While we already have a new picture for them, we can use the top-bottom approach and phrase the problem in the following way: We want to find a mathematical question to which the amplitude is the answer.
As a first step, we need to characterize how the amplitude is invariantly defined in a traditional way. The answer is built in the standard formulation of QFT: the amplitude is specified by properties of locality and unitarity, which translate to simple statements about poles (these are places where the denominator goes to zero). In particular, all poles of M must be sums of external (for integrand also loop) momenta and on these poles M must factorize in a way which is dictated by unitarity. For large class of theories (including our model) this is enough to specify M completely. Reading backwards, if we find a function which satisfies these properties it must be equal to the amplitude. This is a crucial point for us and it guarantees that we calculate the correct object.
Now we consider completely unrelated geometry problem: we define a new geometrical shape – the Amplituhedron. It is something like multi-dimensional polygon embedded in a particular geometrical space, called the Grassmannian. This has a very good motivation in the work done by me and my collaborators in last 5 years on relation between Grassmannians and amplitudes, but I will not explain it here in more details as it would need a separate blog post. Importantly, we can prove that the expression we get for a volume of this object satisfies properties mentioned above and therefore, we can conclude that the scattering amplitudes in our theory are directly related to the volume of Amplituhedron.
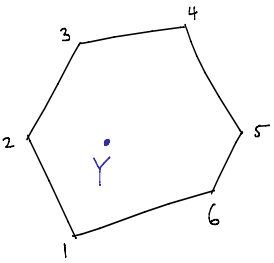This is a basic picture of the whole story but I will try to elaborate it a little more. Many features of the story can be show on a simple example of polygon which is also a simple version of Amplituhedron. Let us consider n points in a (projective) plane and draw a polygon by connecting them in a given ordering. In order to talk about the interior the polygon must be convex which puts some restrictions on these n vertices. Our object is then specified as a set of all points inside a convex polygon.
Now, we want to generalize it to Grassmannian. Instead of points we consider lines, planes, and in general k-planes inside a convex hull (generalization of polygon in higher dimensions). The geometry notion of being “inside” does not really generalize beyond points but there is a precise algebraic statement which directly generalizes from points to k-planes. It is a positivity condition on a matrix of coefficients that we get if we expand a point inside a polygon as linear combination of vertices. In the end, we can define a space of Amplituhedron in the same way as we defined a convex polygon by putting constraints on its vertices (which generalizes convexity) and also positivity conditions on the k-plane (which generalizes notion being inside). In general, there is not a single Amplituhedron but it is rather labeled by three indices: n,k,l. Here n stands for the number of particles, which is equal to a number of vertices, index k captures the helicity structure of the amplitude and it defines a dimensionality of a k-plane which defines a space. Finally, l is the number of loops which translates to the number of lines we have in our configuration space in addition to the k-plane. In the next step we define a volume, more precisely it is a form with logarithmic singularities on the boundaries of this space, and we can show that this function satisfies exactly the same properties as the scattering amplitude. For more details you can read our original paper.
This is a complete reformulation we were looking for. In the definition we do not talk about Lagrangians, Feynman diagrams or locality and unitarity. Our definition is purely geometrical with no reference to physical concepts which all emerge from the shape of Amplituhedron.
Having this definition in hand does not give the answer for amplitudes directly, but it translates the physics problem to purely math problem – calculating volumes. Despite the fact that this object has not been studied by mathematicians at all (there are recent works on the positive Grassmannian of which the Amplituhedron is a substantial generalization), it is reasonable to think that this problem might have a nice general solution which would provide all-loop order results.
There are two main directions in generalization of this story. The first is to try to extend the picture to full (integrated) amplitudes rather than just an integrand. This would definitely require more complicated mathematical structures as would deal now with polylogarithms and their generalizations rather than rational functions. However, already now we have some evidence that the story should extend there as well. The other even more important direction is to generalize this picture to other Quantum field theories. The answer is unclear but if it is positive the picture would need some substantial generalization to capture richness of other QFTs which are absent in our model (like renormalization).
The story of Amplituhedron has an interesting aspect which we always emphasized as a punchline of this program: emergence of locality and unitarity from a shape of this geometrical object, in particular from positivity properties that define it. Of course, amplitudes are local and unitary but this construction shows that these properties might not be fundamental, and can be replaced by a different set of principles from which locality and unitarity follow as derived properties. If this program is successful it might be also an important step to understand quantum gravity. It is well known that quantum mechanics and gravity together make it impossible to have local observables. It is conceivable that if we are able to formulate QFT in the language that does not make any explicit reference to locality, the weak gravity limit of the theory of quantum gravity might land us on this new formulation rather than on the standard path integral formulation. This would not be the first time when the reformulation of the existing theory helped us to do the next step in our understanding of Nature. While Newton’s laws are manifestly deterministic, there is a completely different formulation of classical mechanics – in terms of the principle of the least action – which is not manifestly deterministic. The existence of these very different starting points leading to the same physics was somewhat mysterious to classical physicists, but today we know why the least action formulation exists: the world is quantum-mechanical and not deterministic, and for this reason, the classical limit of quantum mechanics can’t immediately land on Newton’s laws, but must match to some formulation of classical physics where determinism is not a central but derived notion. The least action principle formulation is thus much closer to quantum mechanics than Newton’s laws, and gives a better jumping off point for making the transition to quantum mechanics as a natural deformation, via the path integral.
We may be in a similar situation today. If there is a more fundamental description of physics where space-time and perhaps even the usual formulation of quantum mechanics don’t appear, then even in the limit where non-perturbative gravitational effects can be neglected and the physics reduces to perfectly local and unitary quantum field theory, this description is unlikely to directly reproduce the usual formulation of field theory, but must rather match on to some new formulation of the physics where locality and unitarity are derived notions. Finding such reformulations of standard physics might then better prepare us for the transition to the deeper underlying theory.
Tom — our work does not say anything about the issues you mentioned. It is really about the reformulation of QFT, hopefully in a way that makes some connections to weak-gravity limit of quantum gravity that would address the questions you ask. The reason is that whatever the theory of quantum gravity is — and we do not know the answer yet — it must deal with these issues you discussed, and therefore to formulate a non-gravitational version of it in a way that does not rely explicitly on locality and unitarity might be a good start. It is possible that even if we have amplituhedron construction for all QFTs we will still not see the right path go and for this purpose it will be useless. There is no guarantee here but it seems likely that formulating physics with absence of gravity in a way that makes no explicit reference to spacetime will teach us something important about gravity as well.