I have often talked about the Many-Worlds or Everett approach to quantum mechanics — here’s an explanatory video, an excerpt from From Eternity to Here, and slides from a talk. But I don’t think I’ve ever explained as persuasively as possible why I think it’s the right approach. So that’s what I’m going to try to do here. Although to be honest right off the bat, I’m actually going to tackle a slightly easier problem: explaining why the many-worlds approach is not completely insane, and indeed quite natural. The harder part is explaining why it actually works, which I’ll get to in another post.
Any discussion of Everettian quantum mechanics (“EQM”) comes with the baggage of pre-conceived notions. People have heard of it before, and have instinctive reactions to it, in a way that they don’t have to (for example) effective field theory. Hell, there is even an app, universe splitter, that lets you create new universes from your iPhone. (Seriously.) So we need to start by separating the silly objections to EQM from the serious worries.
The basic silly objection is that EQM postulates too many universes. In quantum mechanics, we can’t deterministically predict the outcomes of measurements. In EQM, that is dealt with by saying that every measurement outcome “happens,” but each in a different “universe” or “world.” Say we think of Schrödinger’s Cat: a sealed box inside of which we have a cat in a quantum superposition of “awake” and “asleep.” (No reason to kill the cat unnecessarily.) Textbook quantum mechanics says that opening the box and observing the cat “collapses the wave function” into one of two possible measurement outcomes, awake or asleep. Everett, by contrast, says that the universe splits in two: in one the cat is awake, and in the other the cat is asleep. Once split, the universes go their own ways, never to interact with each other again.
And to many people, that just seems like too much. Why, this objection goes, would you ever think of inventing a huge — perhaps infinite! — number of different universes, just to describe the simple act of quantum measurement? It might be puzzling, but it’s no reason to lose all anchor to reality.
To see why objections along these lines are wrong-headed, let’s first think about classical mechanics rather than quantum mechanics. And let’s start with one universe: some collection of particles and fields and what have you, in some particular arrangement in space. Classical mechanics describes such a universe as a point in phase space — the collection of all positions and velocities of each particle or field.
What if, for some perverse reason, we wanted to describe two copies of such a universe (perhaps with some tiny difference between them, like an awake cat rather than a sleeping one)? We would have to double the size of phase space — create a mathematical structure that is large enough to describe both universes at once. In classical mechanics, then, it’s quite a bit of work to accommodate extra universes, and you better have a good reason to justify putting in that work. (Inflationary cosmology seems to do it, by implicitly assuming that phase space is already infinitely big.)
That is not what happens in quantum mechanics. The capacity for describing multiple universes is automatically there. We don’t have to add anything.
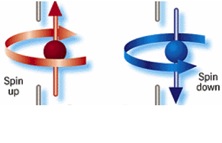The reason why we can state this with such confidence is because of the fundamental reality of quantum mechanics: the existence of superpositions of different possible measurement outcomes. In classical mechanics, we have certain definite possible states, all of which are directly observable. It will be important for what comes later that the system we consider is microscopic, so let’s consider a spinning particle that can have spin-up or spin-down. (It is directly analogous to Schrödinger’s cat: cat=particle, awake=spin-up, asleep=spin-down.) Classically, the possible states are
“spin is up”
or
“spin is down”.
Quantum mechanics says that the state of the particle can be a superposition of both possible measurement outcomes. It’s not that we don’t know whether the spin is up or down; it’s that it’s really in a superposition of both possibilities, at least until we observe it. We can denote such a state like this:
(“spin is up” + “spin is down”).
While classical states are points in phase space, quantum states are “wave functions” that live in something called Hilbert space. Hilbert space is very big — as we will see, it has room for lots of stuff.
To describe measurements, we need to add an observer. It doesn’t need to be a “conscious” observer or anything else that might get Deepak Chopra excited; we just mean a macroscopic measuring apparatus. It could be a living person, but it could just as well be a video camera or even the air in a room. To avoid confusion we’ll just call it the “apparatus.”
In any formulation of quantum mechanics, the apparatus starts in a “ready” state, which is a way of saying “it hasn’t yet looked at the thing it’s going to observe” (i.e., the particle). More specifically, the apparatus is not entangled with the particle; their two states are independent of each other. So the quantum state of the particle+apparatus system starts out like this:
(“spin is up” + “spin is down” ; apparatus says “ready”) (1)
The particle is in a superposition, but the apparatus is not. According to the textbook view, when the apparatus observes the particle, the quantum state collapses onto one of two possibilities:
(“spin is up”; apparatus says “up”)
or
(“spin is down”; apparatus says “down”).
When and how such collapse actually occurs is a bit vague — a huge problem with the textbook approach — but let’s not dig into that right now.
But there is clearly another possibility. If the particle can be in a superposition of two states, then so can the apparatus. So nothing stops us from writing down a state of the form
(spin is up ; apparatus says “up”)
+ (spin is down ; apparatus says “down”). (2)
The plus sign here is crucial. This is not a state representing one alternative or the other, as in the textbook view; it’s a superposition of both possibilities. In this kind of state, the spin of the particle is entangled with the readout of the apparatus.
What would it be like to live in a world with the kind of quantum state we have written in (2)? It might seem a bit unrealistic at first glance; after all, when we observe real-world quantum systems it always feels like we see one outcome or the other. We never think that we ourselves are in a superposition of having achieved different measurement outcomes.
This is where the magic of decoherence comes in. (Everett himself actually had a clever argument that didn’t use decoherence explicitly, but we’ll take a more modern view.) I won’t go into the details here, but the basic idea isn’t too difficult. There are more things in the universe than our particle and the measuring apparatus; there is the rest of the Earth, and for that matter everything in outer space. That stuff — group it all together and call it the “environment” — has a quantum state also. We expect the apparatus to quickly become entangled with the environment, if only because photons and air molecules in the environment will keep bumping into the apparatus. As a result, even though a state of this form is in a superposition, the two different pieces (one with the particle spin-up, one with the particle spin-down) will never be able to interfere with each other. Interference (different parts of the wave function canceling each other out) demands a precise alignment of the quantum states, and once we lose information into the environment that becomes impossible. That’s decoherence.
Once our quantum superposition involves macroscopic systems with many degrees of freedom that become entangled with an even-larger environment, the different terms in that superposition proceed to evolve completely independently of each other. It is as if they have become distinct worlds — because they have. We wouldn’t think of our pre-measurement state (1) as describing two different worlds; it’s just one world, in which the particle is in a superposition. But (2) has two worlds in it. The difference is that we can imagine undoing the superposition in (1) by carefully manipulating the particle, but in (2) the difference between the two branches has diffused into the environment and is lost there forever.
All of this exposition is building up to the following point: in order to describe a quantum state that includes two non-interacting “worlds” as in (2), we didn’t have to add anything at all to our description of the universe, unlike the classical case. All of the ingredients were already there!
Our only assumption was that the apparatus obeys the rules of quantum mechanics just as much as the particle does, which seems to be an extremely mild assumption if we think quantum mechanics is the correct theory of reality. Given that, we know that the particle can be in “spin-up” or “spin-down” states, and we also know that the apparatus can be in “ready” or “measured spin-up” or “measured spin-down” states. And if that’s true, the quantum state has the built-in ability to describe superpositions of non-interacting worlds. Not only did we not need to add anything to make it possible, we had no choice in the matter. The potential for multiple worlds is always there in the quantum state, whether you like it or not.
The next question would be, do multiple-world superpositions of the form written in (2) ever actually come into being? And the answer again is: yes, automatically, without any additional assumptions. It’s just the ordinary evolution of a quantum system according to Schrödinger’s equation. Indeed, the fact that a state that looks like (1) evolves into a state that looks like (2) under Schrödinger’s equation is what we mean when we say “this apparatus measures whether the spin is up or down.”
The conclusion, therefore, is that multiple worlds automatically occur in quantum mechanics. They are an inevitable part of the formalism. The only remaining question is: what are you going to do about it? There are three popular strategies on the market: anger, denial, and acceptance.
The “anger” strategy says “I hate the idea of multiple worlds with such a white-hot passion that I will change the rules of quantum mechanics in order to avoid them.” And people do this! In the four options listed here, both dynamical-collapse theories and hidden-variable theories are straightforward alterations of the conventional picture of quantum mechanics. In dynamical collapse, we change the evolution equation, by adding some explicitly stochastic probability of collapse. In hidden variables, we keep the Schrödinger equation intact, but add new variables — hidden ones, which we know must be explicitly non-local. Of course there is currently zero empirical evidence for these rather ad hoc modifications of the formalism, but hey, you never know.
The “denial” strategy says “The idea of multiple worlds is so profoundly upsetting to me that I will deny the existence of reality in order to escape having to think about it.” Advocates of this approach don’t actually put it that way, but I’m being polemical rather than conciliatory in this particular post. And I don’t think it’s an unfair characterization. This is the quantum Bayesianism approach, or more generally “psi-epistemic” approaches. The idea is to simply deny that the quantum state represents anything about reality; it is merely a way of keeping track of the probability of future measurement outcomes. Is the particle spin-up, or spin-down, or both? Neither! There is no particle, there is no spoon, nor is there the state of the particle’s spin; there is only the probability of seeing the spin in different conditions once one performs a measurement. I advocate listening to David Albert’s take at our WSF panel.
The final strategy is acceptance. That is the Everettian approach. The formalism of quantum mechanics, in this view, consists of quantum states as described above and nothing more, which evolve according to the usual Schrödinger equation and nothing more. The formalism predicts that there are many worlds, so we choose to accept that. This means that the part of reality we experience is an indescribably thin slice of the entire picture, but so be it. Our job as scientists is to formulate the best possible description of the world as it is, not to force the world to bend to our pre-conceptions.
Such brave declarations aren’t enough on their own, of course. The fierce austerity of EQM is attractive, but we still need to verify that its predictions map on to our empirical data. This raises questions that live squarely at the physics/philosophy boundary. Why does the quantum state branch into certain kinds of worlds (e.g., ones where cats are awake or ones where cats are asleep) and not others (where cats are in superpositions of both)? Why are the probabilities that we actually observe given by the Born Rule, which states that the probability equals the wave function squared? In what sense are there probabilities at all, if the theory is completely deterministic?
These are the serious issues for EQM, as opposed to the silly one that “there are just too many universes!” The “why those states?” problem has essentially been solved by the notion of pointer states — quantum states split along lines that are macroscopically robust, which are ultimately delineated by the actual laws of physics (the particles/fields/interactions of the real world). The probability question is trickier, but also (I think) solvable. Decision theory is one attractive approach, and Chip Sebens and I are advocating self-locating uncertainty as a friendly alternative. That’s the subject of a paper we just wrote, which I plan to talk about in a separate post.
There are other silly objections to EQM, of course. The most popular is probably the complaint that it’s not falsifiable. That truly makes no sense. It’s trivial to falsify EQM — just do an experiment that violates the Schrödinger equation or the principle of superposition, which are the only things the theory assumes. Witness a dynamical collapse, or find a hidden variable. Of course we don’t see the other worlds directly, but — in case we haven’t yet driven home the point loudly enough — those other worlds are not added on to the theory. They come out automatically if you believe in quantum mechanics. If you have a physically distinguishable alternative, by all means suggest it — the experimenters would love to hear about it. (And true alternatives, like GRW and Bohmian mechanics, are indeed experimentally distinguishable.)
Sadly, most people who object to EQM do so for the silly reasons, not for the serious ones. But even given the real challenges of the preferred-basis issue and the probability issue, I think EQM is way ahead of any proposed alternative. It takes at face value the minimal conceptual apparatus necessary to account for the world we see, and by doing so it fits all the data we have ever collected. What more do you want from a theory than that?
Professor Carroll, I like your argument that MWI is the interpretation of QM with the least baggage, but I believe the ensemble interpretation has even less baggage as it doesn’t assume the wavefunction ontologically represents any individual system, but instead the abstraction of that system. This seems more in-line with mathematics as a description and not fundamental in the universe, the latter position I feel carries more baggage. What are your reasons for preferring the Everrett many worlds interpretation to the ensemble interpretation?
I figure I’ll add this: (I did some searching and apparently Roger Penrose already made almost the exact same argument as I just did in my last post).
“You want a physical theory that describes the world that we see around us. … Many worlds quantum mechanics doesn’t do that. Either you accept it and try to make sense of it, which is what a lot of people do, or, like me, you say no—that’s beyond the limits of what quantum mechanics can tell us. Which is, surprisingly, a very uncommon position to take. My own view is that quantum mechanics is not exactly right, and I think there’s a lot of evidence for that.”
Daniel,
An interesting paper on the ensemble interpretation.
http://arxiv.org/abs/1308.5290
So I speak from total ignorance of the actual meaning Copenhagen Interpretation but it seems there is at least one question I have never seen discussed. Suppose *two* observers. Assume an observation is the receipt of a photon from the superposition in question. Assume (of course) the photons land on the retinas of the observers in question at exactly the same time (and put them in the same relativistic frame of reference to get that out of the way). So:
* We are done. In which case which observation ‘wins’.
* We are not done. Some Na/K channeling starts happening in each observer’s brain. At some point the brains make on ‘observation’ .. I’ve no idea what that means but I can certainly assert (in this case) that it happens at the same time. Now, what happens to the collapsing wave function …. do both brains agree on the same outcome ? Is this a 50/50 thing … if so why (and where can I find a statement of this tucked inside Schrodinger’s equation …)
Colour me confused …
Whether you bring in a conscious observer or replace him/her by a machine, the very idea of an experiment, which depends ultimately on an arbitrary human judgment (whether to do this experiment today or not) resulting in split universes, is metaphysical at best. It is amusing that this idea comes from Sean who does not believe in religion or metaphysics. Why not be honest and say like Feynman that we do not understand quantum mechanics? Period! This is nothing but a copout. It should not be called an explanation. I would rather believe in multiuniverse coming out of chaotic inflation than arbitrary number of universes brought out by human experimenters on an intrinsically probabilistic natural system.
No physical theory has proven itself to be correct – to think that QM is any different is perhaps foolish.
Compare with Newton’s Gravity where the theory is very useful and can still be used for predictions of satellite orbits, whereas its conceptually completely wrong with its action at a distance and other problems.
Is MWT like satellite orbit prediction? In other words can it still be true if QM is wrong? For many of the alternative theories, where collapse is a real phenomenon (connected to a non linearity, etc) the answer is no, MWT would die along with QM in this case.
Are there _any_ ways to replace QM with a deeper theory so that the MWT could remain?
Contrast the MWT with the distribution in results of an experiment – features like this would obviously survive any new theory, as the experimental record is clear.
Its clear that the ‘phase space’ of replacement theories for QM that allow MWT has to much smaller than those that merely predict experimental outcomes.
Where are all the other universes (especially the ones in which women can’t keep their hands off me)? Are they outside our universe and hence are inaccessible to us?
Are new universes being created all the time or were they all created at the time of our Big Bang?
Thanks
Sean, after producing an excellent recent paper on fine tuning in the early universe, why have you endorsed the silliest theory ever created by the mind of man (the Everett multiple worlds theory, which is more properly called the “infinite duplication theory” or the “infinite excess baggage theory”)? I find it hilarious that putative rationalists such as you do debates arguing against life after death (on the basis of parsimony), and then you go and endorse a theory which is the worst violation of Occam’s Razor in the history of human thinking. You’ve jumped the shark, Sean. Which is a pity, because I was citing some of your recent work approvingly. No person who endorses the Everett multiple worlds theory has any business pretending to be more rational than the flakiest astrologer. Please explain at your next debate on the existence of God or the afterlife that you believe in something 1,000,000,000,000,000,000,000,000,000,000 times more extravagant (and vastly less verifiable) than either hypothesis.
http://www.futureandcosmos.blogspot.com/2013/08/you-are-only-you-no-evidence-for.html
My sincere best wishes, and please disassociate yourself from this mental illness that is the Everett theory. Is it any wonder why people reject science when physicists are endorsing this type of nonsense?
Sean, I am happy to believe many-worlds if all that is at stake is the definition of the word “exist” , which is likely ambiguous in this context anyways. But I am uncomfortable with what seems to me a description too closely tied to single-particle QM. For example, most descriptions I see talk about a split between finite number of options following a measurement arbitrarily localized in space and time. Is there a way to tell the story of universes “splitting” for measurements of operators with a continuous spectrum, like most interesting operators in quantum field theory? Do we get continuous infinity of universes, and if so is there some regularized version and some sense of cut-off independence?
Alanl,
I don’t think your description was complete enough for an answer, so I will assume the following.
A photon is on its way through an apparatus such that it will either strike the retina of one observer or the other (with a nonzero probability for either outcome). It’s wavefunction can be expanded in the following complete basis
{|photon strikes oberver A> , |photon strikes observer B>}
According to the Copenhagen interpretation, the wavefunction of the photon is a tool that encodes the probability of the photon hitting either observer. Both observers will agree on the outcome of the experiment. The “collapse” of the wavefunction is not physical. It is instead an “update” as the observers measure the photon.
According to the Many-World interpretation, there is a universe where the photon strikes observer A, and there is a universe where the photon strikes observer B. The wavefunction does not merely represent a recipe for calculating probabilities. It instead is a more direct description of a reality that includes these two universes.
People do not like the copenhagen interpretation because it does not include a description of the “actualization” of an experiment. Instead, quantum mechanics is seen only as “a matter of relations between phenomena and observations of their frequencies”[1]. A theory that gives a priori probabilities of experimental outcomes, but does not describe how all but one fade to zero.
I would not strictly agree with Sean’s claim that the MW interpretation is the most economical interpretation. I would instead say it is the most economical interpretation that also includes an ontology for actualisation (namely, all possibilities are real, and persist). But I am not convinced quantum mechanics owes us such an ontology. Furthermore, I am not sure it is wise to infer an ontology from our methods of calculation in a regime that is clearly alien to our classical sensibilities. The MWI offers a description of reality independent of experimental phenomena – an ensemble of deterministically evolving possibilites, each of which are as real as the other – but we have no reason to insist such a description of reality must exist.
[1] http://journals.aps.org/rmp/abstract/10.1103/RevModPhys.64.339
Dear Sean, I don’t see how postulating a vast number of (hidden) worlds, with additional postulations on how the worlds split, is simpler and better than just postulating a single pilot wave as Bohm suggested.
Shodan says:
June 30, 2014 at 4:43 pm
Hi Bob,
What is it about the consistent histories description of correlation that you find cringe-worthy? In the CH interpretation, all correlations arise from local interactions, and do not imply any non-local interactions.
——————————————————————————
This I find cringe worthy;
Is quantum mechanics nonlocal?
This depends on what one means by “nonlocal.” Two separated quantum systems A and B can be in an entangled state that lacks any classical analog. However, it is better to think of this as a nonclassical rather than as a nonlocal state, since doing something to system A cannot have any influence on system B as long as the two are sufficiently far apart. In particular, quantum theory gives no support to the notion that the world is infested by mysterious long-range influences that propagate faster thaan the speed of light. Claims to the contrary are based upon an inconsistent or inadequate formulations of quantum principles, typically with reference to measurements. (Also see measurements, Einstein-Podolsky-Rosen.)
http://quantum.phys.cmu.edu/CHS/quest.html#nonlocal
_________________________________
We all know you can’t use the measurement correlations of entangled particles to send information faster than the speed light, but that doesn’t mean there isn’t a non local process involved. That’s what Bell’s theorem proved by the failure to get the predicted inequality in the measurement records. The above just wishes the problem away.
Shodan, that was a very good recommendation, it was a nice summary of the ensemble interpretation. Reading that and I think you’d get a good sense of why I prefer it over many worlds and why I think it’s the more philosophically “simple” interpretation.
I agree with you in your separate comment that I would not assign the wavefunction any fundamental or ontological meaning nor do I believe quantum mechanics on its own implies that we should.
I would also like to add as a separate point that many worlds does not imply that a branching mechanism occurs nor that one is necessary. There are simply many universes of potential outcomes, some that share history up until one such branching point. The relative number (technically measure, not number) of universes with the same outcome for a given event (assuming shared history up until that point) is equal to the probability of an observer being in that particular universe.
Shodan writes
Do you have a link to the studies which show there are more consistent histories than consistent histories that look classical? I was under the impression that, because the probability of a history is derived from the projection operators used to construct the history, all non-classical histories would have zero probability
______________________________
Yes here’s the reference
Properties of Consistent Histories
Fay Dowker, Adrian Kent
(Submitted on 17 Sep 1994 (v1), last revised 30 Jan 1996 (this version, v4))
Here is a response to this.
Equivalent Sets of Histories and Multiple Quasiclassical Realms
Murray Gell-Mann, James B. Hartle (Santa Fe Institute, Los Alamos, and University of New Mexico)
(Submitted on 8 Apr 1994 (v1), last revised 5 May 1996 (this version, v3))
Bob,
I would emphatically object to the insistence that the intepretation involves some ambiguous non-local “process”. The CH interpretation explicitly rejects the attachment of any physical process to the reduction of the wavefunction. Bell’s theorem did not prove the existence of non-local processes. Instead, it proved that any realist interpretation of QM must involve non-local processes. (See section 8 of this paper: http://arxiv.org/pdf/1308.5290v2.pdf )
Daniel,
I completely agree. The “branching” of worlds is effectively an increase in hamming distance that occurs via decoherence, a unitary process. No new mechanism is postulated.
Shodan says:
June 30, 2014 at 10:17 pm
Bob,
I would emphatically object to the insistence that the interpretation involves some ambiguous non-local “process”. The CH interpretation explicitly rejects the attachment of any physical process to the reduction of the wavefunction. Bell’s theorem did not prove the existence of non-local processes. Instead, it proved that any realist interpretation of QM must involve non-local processes. (See section 8 of this paper: http://arxiv.org/pdf/1308.5290v2.pdf )
____________________________
I think logic compels us to view the failure to get the inequality devised by Bell in the correlated measurement record for the entangled particles to accept the fact that a measurement of one particle affects the measurement result of the other instantly. The whole premise of Bell’s inequality is based on the absence of non local influences. Of course since these measurement events are space like separated which particle effects the other is frame dependent, but I don’t think this provides an escape from accepting a non local effect at work in QM.
Bob,
I wouldn’t take action at a distance to be the necessary conclusion of bell’s inequality, as such a violation of the inequality can be derived from experiments which take place only in unitary representations of SU(2), which as a group contains no intrinsic concept of locality.
Pingback: Measuring the ‘reality’ | The Great Vindications
Bob,
I would instead say the logic compels us to accept either-or. If we reject a realist interpretation of QM, then any obligation to suppose non-local interactions leaves with it.
Bell’s theorem is
“No physical theory of local hidden variables can ever produce all of the predictions of QM”[1]
which is very different from
“No local theory can ever produce all of the predictions of QM”
In fact, I have previously come across a Nature paper claiming the choice is even more restricted, and non-local realism must be rejected[2] (Though I have not thoroughly read it yet.)
[1]http://en.wikipedia.org/wiki/Bell%27s_theorem
[2]http://arxiv.org/abs/0704.2529
Shodan,
sorry I wasn’t too clear — I guess thatis the nature of this beast, but you say:
“I don’t think your description was complete enough for an answer, so I will assume the following.
A photon is on its way through an apparatus such that it will either strike the retina of one observer or the other (with a nonzero probability for either outcome). ”
My point (question, whatever) is that it seems to me that all Copenahagen Interpretations begin this way — ONE observer, one photon. But our putative S.Cat reflects many photons when the box is open, so certainly there must be cases where two photons (which somehow carry the notion of an observation) hit whatever they have to hit in two different observers (in the same frame of reference) to become an ‘observation’ at exactly the same time – albeit in two different observers. So, do they agree on the outcome ? — it would seem so in the standard interpretation, but I cannot fathom why this should be so (50/50 independently for each observer, surely). If one observer got the photon even slightly before the other, then I guess he takes the other’s superposition down with him, but in a spot-on-dead-even-tie (don’t know what that means, but anyway) either:
* They both agree (and then what happened to 50/50 independently ?), or
* They both have their own interpretations of the result, and in the 50% of the cases where they disagree the universe forks
I’m not sure I like either of these .. 🙂
The reason why I don’t believe in many worlds interpretation is that I don’t see it around me. The universe I observe is the universe where all quantum effects cancel out nicely. If that interpretation is true, there’s countless universes where 3D cinemas went bankrupt because polarizing glasses stopped working. Because photoreceptor cells in my eyes are measuring all those photons coming through them one after another. And despite the sheer size of that ‘true path’ universe set where things go on fine, I just refuse to accept the idea that somewhere out there is a copy of me unable to watch 3D movies because the left 3D glasses filter stays mostly dark all the time for no apparent reason, just to make our universe complete.
Dear Sean,
Thank you for your clear article on EQM. There are some things on which I would really like some more exposition:
“We wouldn’t think of our pre-measurement state (1) as describing two different worlds; it’s just one world, in which the particle is in a superposition. But (2) has two worlds in it. The difference is that we can imagine undoing the superposition in (1) by carefully manipulating the particle, but in (2) the difference between the two branches has diffused into the environment and is lost there forever.”
“The difference is that we can imagine undoing the superposition in (1) by carefully manipulating the particle, but in (2) the difference between the two branches has diffused into the environment and is lost there forever.”
There seems to be some additional postulate (physical or at least philosophical) to the quantum formalism that you introduce here. In principle, if the superposition is diffused into the environment then, due to the unitary nature of quantum mechanics, the inverse time evolution should always be possible. The off-diagonal terms in the density matrix will never be truly zero, just for all practical purposes (decoherence). (Similar to discussions of irreversibility in statistical mechanics) In other words, according to quantum mechanics two universes should be able to sometimes “fuse” back into a superposition. Furthermore, there seems to be no rigorous point that one can say a new branch universe has been created if mathematically one can only say that on a local level it seems as though the two possibilities of a subsystem of our universe become increasingly less correlated.
To me it seems that at some point when superpositions become very non-local and extended throughout the environment, you suddenly postulate different universes! I think this does not make sense. You say that because of decoherence they become independent, however, this is for all practical purposes and only on the local level it seems this way. Surely you must agree that the complete superposition is still out there in this single universe?
Yours sincerely,
Jasper
My apologies for the problems with emphasis in the reply above.
A question which really puzzles me about the Everett interpretation: can probabilities of superposed states be irrational, for example 1/pi? If so how will the universe split into distinct number of sub universes? Perhaps my premise is incorrect, not sure, any comments much appreciated. Thanks.