One of the most profound and mysterious principles in all of physics is the Born Rule, named after Max Born. In quantum mechanics, particles don’t have classical properties like “position” or “momentum”; rather, there is a wave function that assigns a (complex) number, called the “amplitude,” to each possible measurement outcome. The Born Rule is then very simple: it says that the probability of obtaining any possible measurement outcome is equal to the square of the corresponding amplitude. (The wave function is just the set of all the amplitudes.)
Born Rule: ![]()
The Born Rule is certainly correct, as far as all of our experimental efforts have been able to discern. But why? Born himself kind of stumbled onto his Rule. Here is an excerpt from his 1926 paper:
That’s right. Born’s paper was rejected at first, and when it was later accepted by another journal, he didn’t even get the Born Rule right. At first he said the probability was equal to the amplitude, and only in an added footnote did he correct it to being the amplitude squared. And a good thing, too, since amplitudes can be negative or even imaginary!
The status of the Born Rule depends greatly on one’s preferred formulation of quantum mechanics. When we teach quantum mechanics to undergraduate physics majors, we generally give them a list of postulates that goes something like this:
- Quantum states are represented by wave functions, which are vectors in a mathematical space called Hilbert space.
- Wave functions evolve in time according to the Schrödinger equation.
- The act of measuring a quantum system returns a number, known as the eigenvalue of the quantity being measured.
- The probability of getting any particular eigenvalue is equal to the square of the amplitude for that eigenvalue.
- After the measurement is performed, the wave function “collapses” to a new state in which the wave function is localized precisely on the observed eigenvalue (as opposed to being in a superposition of many different possibilities).
It’s an ungainly mess, we all agree. You see that the Born Rule is simply postulated right there, as #4. Perhaps we can do better.
Of course we can do better, since “textbook quantum mechanics” is an embarrassment. There are other formulations, and you know that my own favorite is Everettian (“Many-Worlds”) quantum mechanics. (I’m sorry I was too busy to contribute to the active comment thread on that post. On the other hand, a vanishingly small percentage of the 200+ comments actually addressed the point of the article, which was that the potential for many worlds is automatically there in the wave function no matter what formulation you favor. Everett simply takes them seriously, while alternatives need to go to extra efforts to erase them. As Ted Bunn argues, Everett is just “quantum mechanics,” while collapse formulations should be called “disappearing-worlds interpretations.”)
Like the textbook formulation, Everettian quantum mechanics also comes with a list of postulates. Here it is:
- Quantum states are represented by wave functions, which are vectors in a mathematical space called Hilbert space.
- Wave functions evolve in time according to the Schrödinger equation.
That’s it! Quite a bit simpler — and the two postulates are exactly the same as the first two of the textbook approach. Everett, in other words, is claiming that all the weird stuff about “measurement” and “wave function collapse” in the conventional way of thinking about quantum mechanics isn’t something we need to add on; it comes out automatically from the formalism.
The trickiest thing to extract from the formalism is the Born Rule. That’s what Charles (“Chip”) Sebens and I tackled in our recent paper:
Self-Locating Uncertainty and the Origin of Probability in Everettian Quantum Mechanics
Charles T. Sebens, Sean M. CarrollA longstanding issue in attempts to understand the Everett (Many-Worlds) approach to quantum mechanics is the origin of the Born rule: why is the probability given by the square of the amplitude? Following Vaidman, we note that observers are in a position of self-locating uncertainty during the period between the branches of the wave function splitting via decoherence and the observer registering the outcome of the measurement. In this period it is tempting to regard each branch as equiprobable, but we give new reasons why that would be inadvisable. Applying lessons from this analysis, we demonstrate (using arguments similar to those in Zurek’s envariance-based derivation) that the Born rule is the uniquely rational way of apportioning credence in Everettian quantum mechanics. In particular, we rely on a single key principle: changes purely to the environment do not affect the probabilities one ought to assign to measurement outcomes in a local subsystem. We arrive at a method for assigning probabilities in cases that involve both classical and quantum self-locating uncertainty. This method provides unique answers to quantum Sleeping Beauty problems, as well as a well-defined procedure for calculating probabilities in quantum cosmological multiverses with multiple similar observers.
Chip is a graduate student in the philosophy department at Michigan, which is great because this work lies squarely at the boundary of physics and philosophy. (I guess it is possible.) The paper itself leans more toward the philosophical side of things; if you are a physicist who just wants the equations, we have a shorter conference proceeding.
Before explaining what we did, let me first say a bit about why there’s a puzzle at all. Let’s think about the wave function for a spin, a spin-measuring apparatus, and an environment (the rest of the world). It might initially take the form
(α[up] + β[down] ; apparatus says “ready” ; environment0). (1)
This might look a little cryptic if you’re not used to it, but it’s not too hard to grasp the gist. The first slot refers to the spin. It is in a superposition of “up” and “down.” The Greek letters α and β are the amplitudes that specify the wave function for those two possibilities. The second slot refers to the apparatus just sitting there in its ready state, and the third slot likewise refers to the environment. By the Born Rule, when we make a measurement the probability of seeing spin-up is |α|2, while the probability for seeing spin-down is |β|2.
In Everettian quantum mechanics (EQM), wave functions never collapse. The one we’ve written will smoothly evolve into something that looks like this:
α([up] ; apparatus says “up” ; environment1)
+ β([down] ; apparatus says “down” ; environment2). (2)
This is an extremely simplified situation, of course, but it is meant to convey the basic appearance of two separate “worlds.” The wave function has split into branches that don’t ever talk to each other, because the two environment states are different and will stay that way. A state like this simply arises from normal Schrödinger evolution from the state we started with.
So here is the problem. After the splitting from (1) to (2), the wave function coefficients α and β just kind of go along for the ride. If you find yourself in the branch where the spin is up, your coefficient is α, but so what? How do you know what kind of coefficient is sitting outside the branch you are living on? All you know is that there was one branch and now there are two. If anything, shouldn’t we declare them to be equally likely (so-called “branch-counting”)? For that matter, in what sense are there probabilities at all? There was nothing stochastic or random about any of this process, the entire evolution was perfectly deterministic. It’s not right to say “Before the measurement, I didn’t know which branch I was going to end up on.” You know precisely that one copy of your future self will appear on each branch. Why in the world should we be talking about probabilities?
Note that the pressing question is not so much “Why is the probability given by the wave function squared, rather than the absolute value of the wave function, or the wave function to the fourth, or whatever?” as it is “Why is there a particular probability rule at all, since the theory is deterministic?” Indeed, once you accept that there should be some specific probability rule, it’s practically guaranteed to be the Born Rule. There is a result called Gleason’s Theorem, which says roughly that the Born Rule is the only consistent probability rule you can conceivably have that depends on the wave function alone. So the real question is not “Why squared?”, it’s “Whence probability?”
Of course, there are promising answers. Perhaps the most well-known is the approach developed by Deutsch and Wallace based on decision theory. There, the approach to probability is essentially operational: given the setup of Everettian quantum mechanics, how should a rational person behave, in terms of making bets and predicting experimental outcomes, etc.? They show that there is one unique answer, which is given by the Born Rule. In other words, the question “Whence probability?” is sidestepped by arguing that reasonable people in an Everettian universe will act as if there are probabilities that obey the Born Rule. Which may be good enough.
But it might not convince everyone, so there are alternatives. One of my favorites is Wojciech Zurek’s approach based on “envariance.” Rather than using words like “decision theory” and “rationality” that make physicists nervous, Zurek claims that the underlying symmetries of quantum mechanics pick out the Born Rule uniquely. It’s very pretty, and I encourage anyone who knows a little QM to have a look at Zurek’s paper. But it is subject to the criticism that it doesn’t really teach us anything that we didn’t already know from Gleason’s theorem. That is, Zurek gives us more reason to think that the Born Rule is uniquely preferred by quantum mechanics, but it doesn’t really help with the deeper question of why we should think of EQM as a theory of probabilities at all.
Here is where Chip and I try to contribute something. We use the idea of “self-locating uncertainty,” which has been much discussed in the philosophical literature, and has been applied to quantum mechanics by Lev Vaidman. Self-locating uncertainty occurs when you know that there multiple observers in the universe who find themselves in exactly the same conditions that you are in right now — but you don’t know which one of these observers you are. That can happen in “big universe” cosmology, where it leads to the measure problem. But it automatically happens in EQM, whether you like it or not.
Think of observing the spin of a particle, as in our example above. The steps are:
- Everything is in its starting state, before the measurement.
- The apparatus interacts with the system to be observed and becomes entangled. (“Pre-measurement.”)
- The apparatus becomes entangled with the environment, branching the wave function. (“Decoherence.”)
- The observer reads off the result of the measurement from the apparatus.
The point is that in between steps 3. and 4., the wave function of the universe has branched into two, but the observer doesn’t yet know which branch they are on. There are two copies of the observer that are in identical states, even though they’re part of different “worlds.” That’s the moment of self-locating uncertainty. Here it is in equations, although I don’t think it’s much help.
You might say “What if I am the apparatus myself?” That is, what if I observe the outcome directly, without any intermediating macroscopic equipment? Nice try, but no dice. That’s because decoherence happens incredibly quickly. Even if you take the extreme case where you look at the spin directly with your eyeball, the time it takes the state of your eye to decohere is about 10-21 seconds, whereas the timescales associated with the signal reaching your brain are measured in tens of milliseconds. Self-locating uncertainty is inevitable in Everettian quantum mechanics. In that sense, probability is inevitable, even though the theory is deterministic — in the phase of uncertainty, we need to assign probabilities to finding ourselves on different branches.
So what do we do about it? As I mentioned, there’s been a lot of work on how to deal with self-locating uncertainty, i.e. how to apportion credences (degrees of belief) to different possible locations for yourself in a big universe. One influential paper is by Adam Elga, and comes with the charming title of “Defeating Dr. Evil With Self-Locating Belief.” (Philosophers have more fun with their titles than physicists do.) Elga argues for a principle of Indifference: if there are truly multiple copies of you in the world, you should assume equal likelihood for being any one of them. Crucially, Elga doesn’t simply assert Indifference; he actually derives it, under a simple set of assumptions that would seem to be the kind of minimal principles of reasoning any rational person should be ready to use.
But there is a problem! Naïvely, applying Indifference to quantum mechanics just leads to branch-counting — if you assign equal probability to every possible appearance of equivalent observers, and there are two branches, each branch should get equal probability. But that’s a disaster; it says we should simply ignore the amplitudes entirely, rather than using the Born Rule. This bit of tension has led to some worry among philosophers who worry about such things.
Resolving this tension is perhaps the most useful thing Chip and I do in our paper. Rather than naïvely applying Indifference to quantum mechanics, we go back to the “simple assumptions” and try to derive it from scratch. We were able to pinpoint one hidden assumption that seems quite innocent, but actually does all the heavy lifting when it comes to quantum mechanics. We call it the “Epistemic Separability Principle,” or ESP for short. Here is the informal version (see paper for pedantic careful formulations):
ESP: The credence one should assign to being any one of several observers having identical experiences is independent of features of the environment that aren’t affecting the observers.
That is, the probabilities you assign to things happening in your lab, whatever they may be, should be exactly the same if we tweak the universe just a bit by moving around some rocks on a planet orbiting a star in the Andromeda galaxy. ESP simply asserts that our knowledge is separable: how we talk about what happens here is independent of what is happening far away. (Our system here can still be entangled with some system far away; under unitary evolution, changing that far-away system doesn’t change the entanglement.)
The ESP is quite a mild assumption, and to me it seems like a necessary part of being able to think of the universe as consisting of separate pieces. If you can’t assign credences locally without knowing about the state of the whole universe, there’s no real sense in which the rest of the world is really separate from you. It is certainly implicitly used by Elga (he assumes that credences are unchanged by some hidden person tossing a coin).
With this assumption in hand, we are able to demonstrate that Indifference does not apply to branching quantum worlds in a straightforward way. Indeed, we show that you should assign equal credences to two different branches if and only if the amplitudes for each branch are precisely equal! That’s because the proof of Indifference relies on shifting around different parts of the state of the universe and demanding that the answers to local questions not be altered; it turns out that this only works in quantum mechanics if the amplitudes are equal, which is certainly consistent with the Born Rule.
See the papers for the actual argument — it’s straightforward but a little tedious. The basic idea is that you set up a situation in which more than one quantum object is measured at the same time, and you ask what happens when you consider different objects to be “the system you will look at” versus “part of the environment.” If you want there to be a consistent way of assigning credences in all cases, you are led inevitably to equal probabilities when (and only when) the amplitudes are equal.
What if the amplitudes for the two branches are not equal? Here we can borrow some math from Zurek. (Indeed, our argument can be thought of as a love child of Vaidman and Zurek, with Elga as midwife.) In his envariance paper, Zurek shows how to start with a case of unequal amplitudes and reduce it to the case of many more branches with equal amplitudes. The number of these pseudo-branches you need is proportional to — wait for it — the square of the amplitude. Thus, you get out the full Born Rule, simply by demanding that we assign credences in situations of self-locating uncertainty in a way that is consistent with ESP.
We like this derivation in part because it treats probabilities as epistemic (statements about our knowledge of the world), not merely operational. Quantum probabilities are really credences — statements about the best degree of belief we can assign in conditions of uncertainty — rather than statements about truly stochastic dynamics or frequencies in the limit of an infinite number of outcomes. But these degrees of belief aren’t completely subjective in the conventional sense, either; there is a uniquely rational choice for how to assign them.
Working on this project has increased my own personal credence in the correctness of the Everett approach to quantum mechanics from “pretty high” to “extremely high indeed.” There are still puzzles to be worked out, no doubt, especially around the issues of exactly how and when branching happens, and how branching structures are best defined. (I’m off to a workshop next month to think about precisely these questions.) But these seem like relatively tractable technical challenges to me, rather than looming deal-breakers. EQM is an incredibly simple theory that (I can now argue in good faith) makes sense and fits the data. Now it’s just a matter of convincing the rest of the world!

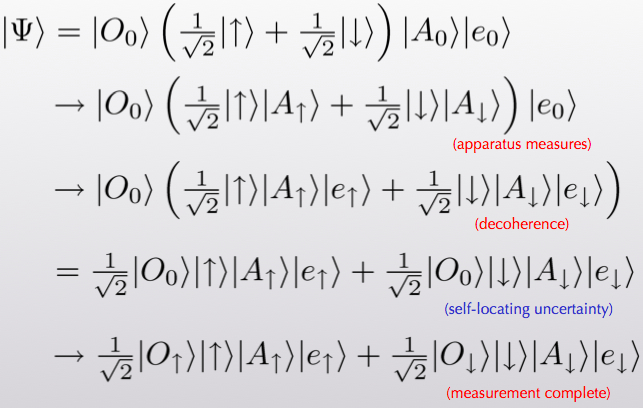
Sean, perhaps this concern is besides the point, but let me rephrase my discomfort with the discrete nature of the story the MWI tells. As you explained extremely well here, the same physical system can have multiple descriptions, each appropriate for experiments done at different length or energy scale. So suppose we look at scattering of protons and use our detector to measure some aspect of the final state. How many “worlds” do we have in the end? Do we think about all possible states of the final proton, or the vastly more complex story in terms of fluctuating quarks and gluons (which certainly interacted strongly with the measuring device)? Preferably those stories equivalent in some sense, but I am not sure in what precise sense they are.
Sean you are a cosmologist so you can be forgiven for taking Many-Worlds seriously.
All you have done is drop qm axiom #4 and replaced it with amplitudes and ESP. But we may just as well drop other of the qm axioms and get other realist interpretations instead (e.g Bohmianism or GRW).
And it would be nice if you addressed the fact that our free choice of measurement leads to the set of possible outcomes, so that, in a sense, humans decide which universes are created in the splitting. But that’s odd!
I have a bit of a far-out question. In the path integral approach to QM, we see that two possibilities interfere — both contribute to the final amplitude before it is squared — only if they can converge onto the same physical state. All the ways of getting from the same state to the same state interfere. I assume that is equivalent to being entangled, but perhaps I am misunderstanding that. So the idea that two branches have split means, as I understand it, that there is no (or vanishingly small) possibility of them evolving to the same state.
Now, to throw in something I really know nothing about, I am vaguely aware that there are “bouncing universe” theories of cosmology. What I am wondering is if they involve different branches all converging on the same final state — which I imagine means non-unitary evolution, information being lost, which seems like it couldn’t be. But it seems like to be viable, these bouncing universe theories must get you back to a low-entropy post-bounce initial condition, and it’s a little hard to imagine how that could happen if that initial condition retained all the information specifying exactly which branch you were on before the bounce.
So that’s the vague understanding behind my question, but to state my question simply: in bouncing universe scenarios, do different branches converge on the same final state at the bounce? And if they do, doesn’t that mean they are entangled?
“Now it’s just a matter of convincing the rest of the world!” , I wouls say not to worry about convincing anybody since in infinite number of universes you have already convinced everybody.
You just happen to be in wrong infinity 🙂 .
I am a layperson here also, a Physician fascinated by cosmology, listened to all the Teaching Company courses related to physics and read all the cosmology books aimed at lay people. I have a reasonably good grasp on the wave function and collapse of the wave function for small particles- how that leads to electron tunneling and other strange but true phenomena.
I absolutely cannot grasp the thought that there is a wave function for a complex large object. Sean used an orange in one of his lectures. Really? How about an animal? On a microscopic level the many parts of an orange or parts of an animal aren’t even close to each other. Can something larger than a molecule really have just one wave function?
I would be so appreciative if any of the physicists here could help me understand this question. Thank-you.
“a vanishingly small percentage of the 200+ comments actually addressed the point of the article”
What were the chances?
Jerry, I have two answers to your question. First, the simplest example of a wave function for a single particle confined to a 1-dimensional box is not just the wave function for the particle, it is the wave function for the particle confined to a box of a given size. Choose a box of a different size and you get a different wave function. The box can be a micron or a mile or lightyear in length.
But getting back to the wave function for the orange, the wave function would be the wave function for all the atoms in the orange. psi = psi(x1,x2,… xN). Then the probability of finding particle 1 near x1 particle 2 near x2, etc is given by the magnitude of psi squared.
The wave function for the many-particle orange is a vastly more complicated object than the wave function for a single particle in a box. But even in the simple case of a lone particle in a box the wave function is not just for the particle it is for the box/particle system and the box can be enormous.
Thank-you John-
That makes so much more sense to me than to think of the wave function of the orange as a whole to be the same as to that of an electron or proton.
Now, since the atoms inside the orange are interacting with each other- isn’t that a measurement? Isn’t that an “Observation”? Doesn’t that collapse the wave function for the orange as a whole? Even though we can’t know the position and momentum of each electron or quark in the orange, don’t we now know the position and momentum of the orange?
Moshe– The “how many worlds” question is a good one, when we think about realistic situations. (I’ve heard experts say it’s just not a well-defined question, but I haven’t completely understood the argument.) But there’s no ambiguity concerning e.g. protons vs. quarks. You just look at what is entangled with what. In an ordinary nucleon, the quarks and gluons are entangled with each other in a very particular way to make the lowest-lying state. That state just has a couple of remaining quantum numbers (spin, position) that can possibly entangle with the outside world and lead to decoherent branches.
Jerry– According to quantum mechanics of any sort, there is actually only one wave function for the entire universe. Each living being is a part of it, just like each atom or particle is.
Does this analogy help Jerry: when you listen to a symphony orchestra, there’s just one soundwave detected by your ears. It’s the brain that interprets that wave as a combination of violins, flutes, horns, oboes etc., and the better your musical ear the more easily you can mentally separate the wave that came into your ear into its constituent causes. If your “ear” is especially discriminating, you can attend to individual harmonics of a single instrument–but this is all in the interpretation; the pressure wave (“soundwave”) could be decomposed into sinusoidal components in any number of ways. The analogy, then, is that there’s a single wave function for the entire universe, but we can interpret parts of it to be associated with various smaller things (like cats) and sub-things (like their whiskers) and sub-sub-things (molecules)–etc. etc.
The reliance on entanglement would work well with LQG. It would be interesting if entanglement, long ignored, was this grand mechanism responsible for dynamic interaction.
Zurek is definitely worth a read.
Experimentally studying the boundary of coherence – decoherence is vitally important. If anything, these studies have practical benefit to see how ‘macroscopic’ we can begin to manipulate entangled states.
I am curious if there are any known ways to stimulate emission of 3.55 keV photons (like those described here http://arxiv.org/abs/1402.2301)? In light of this discussion: what part of our universe can make such states if there are no known atoms (machinery) or coherent interactions with fields that generate them. Is it some complex quantum mechanical explanation, or is it more likely a semi-classical explanation for the presence of such an x-ray line?
I think that a lot of the problems that people have with the multiple worlds idea (and really to quantum mechanics in general) are related to time. Things are usually presented as distinct worlds branching or splitting to become separate worlds, (or collapse occurring) and this happens “as time goes by”. I will try to quickly put together a string of thoughts here, but certainly it won’t be very clear. Hopefully just writing something down clarifies things in my own mind a little bit. Sorry if I start rambling.
I think it is very useful to think about physics (and the nature of reality) from the basic point of view that time doesn’t flow at all, and what we usually think of as time is not really a singular uni-directional phenomenon.
Most quantum mechanics examples and experiments use microscopic particles. Time is easily shown to have no preferred direction for microscopic particles. The examples used to show this are clear only because of the small numbers of possible options in each direction of time. As soon as one direction starts to have many more possible states than the other, then you can tell which is the future and which is the past. The future just has more options than the past, that is why it is the future.
These options are actually the components of entropy. It isn’t that there is just more entropy in the future, rather, the future is simply defined by the fact that it is the direction of more options.
But what does that really mean? It probably means that in the ‘future’ direction, the universal wave function has more small scale structure. More parts of it behave independently, or have decoherence with other parts. This is the ‘splitting’ of worlds. These decoherent branches are the ‘options’ that define entropy. Without distinct options, entropy doesn’t make sense, and time doesn’t appear to flow in one direction.
Of course the ‘time flowing’ and ‘world splitting’ are just illusions resulting from our position in the system. All of the branches actually do interact with each other, it is just mostly in the direction that we call the ‘past’.
It is only because we ourselves are actually a small part of this large system that we can not see the time independence. We are constrained by the decoherent structure to only be able to observe toward the past direction. This is what makes quantum mechanics and relativity seem difficult and illogical to people.
Most of the difficult to grasp principles of quantum mechanics are made simpler if you think of time as just another direction. Take the EPR paradox; where the measurement of a state of an entangled particle “instantaneously” determines the result of a measurement separated by a distance of millions of light years (seemingly faster the speed of light). The problem is the use of the term instantaneous. These particles can ‘move’ backward in time as easily as forward in time (just as they can ‘move’ up or down, or left or right).
If you think of ‘the outcome’ of the final measurement of one of the particles traveling backwards in time (physically with the particle), to the point where the entanglement occurred, and then forward in time with the other particle to when that one is measured (and vice versa), then there is never any action at a distance. All actions are local. This seems strange, but it is only because we can’t see the whole picture.
Quantum mechanical interactions are actually very similar to classical interactions, IF you consider time to be the same as the other spacial dimensions. The complication arises because time seems to have a property that differentiates it from the other dimensions: there are more options in one direction versus the other. However, this is also an illusion.
All of these dimensions are actually part of the same ‘thing’ which is the universal wave function. What we see as ‘THE time dimension’ is just whichever direction has the most options when seen from any particular spot. Time is defined by the entropy, which is defined by the decoherence branches of the wave function.
Time dilation and length contraction in special relativity are what you start to observe when more than one dimension starts to have a large number of options (decoherence branches). It is no longer so obvious which direction is the “time” dimension. You can then see that ‘before’ and ‘after’ are not definite things, but it is nonetheless always a consistent system because it is all one wave function.
While it isn’t totally clear how to put gravity and general relativity together with quantum mechanics, that is surely because of the issues of thinking about movement, velocity, and acceleration when time is not a distinct parameter.
Clearly some types of particles interact with other particles not only in the classical three dimensions, but rather in four dimensions, such that the time dimension for these interactions is not in exactly the same direction as the bulk of the surrounding particles. This can lead to seemingly stationary particles experiencing acceleration, such as gravity.
Applying this same kind of thought to the many worlds interpretation makes it easier to see that all of the ‘worlds’ do interact with each other, but mostly through the ‘past’ direction. The separate ‘worlds’ are only separate from our point of view. There is no need to worry about conservation of energy or mass or whatever people get hung up on. Everything is part of the same wave function, which is time independent.
Shawn,
Hope you will share results from the workshop on when and how branching occurs when you have time. I guess they’re technical issues to the faithful but may seem more fundamental to the agnostics.
Thanks for the great blog.
As a theory, Many Worlds is in a bad state, and this paper is an example of why.
If someone tells me that there are many quantum worlds in a single wavefunction, I expect that they can tell me exactly what part of a wavefunction is a world, and how many worlds there are in a given wavefunction.
As Sean says in his article, a naive attempt to be concrete about what a world is, and how many there are in a given wavefunction, leads to something which *disagrees* with experiment.
But rather than regard this as a point against Many Worlds, and rather than try new ways to carve up the wavefunction into definite worlds… instead we have contorted sophistical arguments about how you should *think* in a multiverse, as the explanation of the Born rule.
The intellectual decline comes when people stop regarding Born probabilities as frequencies, and stop wanting a straightforward theory in which you can “count the worlds”.
Common sense tells me that if A is observed happening twice as often as B, and if we are to believe in parallel universes, then there ought to be twice as many universes where A happens, or where A is seen to happen. But a detailed multiverse theory in which this is the case is hard to construct (Robin Hanson is one of the few to have tried).
Instead what we are getting (from Deutsch, from Wallace, now here) are these rambling arguments about decision theory, rationality, and epistemology in a multiverse. They all aim to produce a conclusion of the form, “you should think that A is twice as likely as B”, without having to exhibit a clear picture of reality in which A-worlds are twice as *common* as B-worlds.
A technical debunking of such arguments always ought to be possible. In the present case, it must have something to do with the use of these epistemic principles, “Indifference” vs “ESP”, but I still haven’t decoded it. What I want to do in this comment, is just to arm the reader with a general defense against this pernicious new trend in Many Worlds apologetics.
My suggested rule of thumb is this: if a Many Worlds theory *doesn’t* explain the Born rule by counting worlds, look upon it with suspicion, or just ignore it.
P.S. Sean cites Gleason’s theorem as a reason to think that probabilities in a quantum multiverse must come from the square of the amplitude. So please, Everett fans, why not try to come up with an exact and objective theory about how the wavefunction subdivides into worlds, that is somehow inspired by Gleason’s theorem? Rather than spreading confusion and an illusion of understanding.
Mitchell Porter,
“If someone tells me that there are many quantum worlds in a single wavefunction, I expect that they can tell me exactly what part of a wavefunction is a world, and how many worlds there are in a given wavefunction.”
If there were a way to specify which part of the wavefunction is “a world”, it would be (more or less) straightforward to count how many of them are there, and use their frequencies as probabilities. Due to the separability axiom for the Hilbert space in QM, there would be at most countably infinitely many “worlds” in a given wavefunction, and the number of appearances of each particular “world” could be, well, counted.
But the main problem of MWI is that actually there is no way to specify which part of the wavefunction is “a world”. This is a serious problem of MWI, acknowledged by MWI fans (including even Sean, although he tries his best to avoid talking about it), and is called “the pointer basis problem”. It is the raison d’etre for all those additional axioms in the textbook version of QM, as compared to MWI. It lies at the core of the measurement problem and the Schrodinger cat paradox (see my previous comment).
MWI, as it stands, has no solution to this problem, and it can be resolved only by postulating additional axioms. These additional axioms will in turn kill the argument of parsimony that MWI fans are so fond of.
HTH, 🙂
Marko
Is there an experimental test for the MWI? Can it be falsified?
I do not believe there is any logical pathway from Schrodinger’s equation describing a quantum system to there must be many universes in which every possible outcome of every “measurement” that has ever taken place is realized.
Instead, we need to treat Schrodinger’s equation as a model that works, not as absolute “gospel”. The Copenhagen Interpretation, as far as I’m concerned, is a model, and a very good one. And that’s all that we can ever hope to achieve in science. If we find a set of equations that accounts for observations, then we are doing good science. However, we shouldn’t overly extend those equations to a point wherein there is no logical pathway joining the two together.
For example, a typical optimization problem in first year calculus is finding the length of a rectangle that maximizes area, given certain constraints. Usually, we need to solve a quadratic equation for the length, and we get a positive solution, and a negative solution. The positive solution is the correct, physically relevant solution, and the negative solution is not physically relevant. We don’t take every mathematical solution seriously. Just because it comes out of the math, doesn’t mean it’s right. If, somehow, many worlds comes out of quantum mechanics, doesn’t mean it’s right. Our mathematics serve as useful models, and nothing more. There is no logical pathway from quadratic equation to negative length. In turn, there is no logical pathway from Schrodinger’s equation to many worlds.
About HOW MANY multiverses, I would like to present the next thoughts about how we could measure this, related to MaxTegmark’s proposing: “Is there a copy of you reading this article?” inside other anti-material or material ( Charge Prity symmetric) COPY universes.
The idea:
Benjamin Libet measured the so called electric Readiness Potential (RP) time to perform a volitional act, in the brains of his students and the time of conscious awareness (TCA) of that act, which appeared to come 500 m.sec behind the RP. The “volitional act” was in principle based on the free choice to press an electric bell button. The results of this experiment gives still an ongoing debate in the broad layers of the scientific community, because the results are still (also in recent experiments) in firm contrast with the expected idea of Free Will and causality. However in this essay I propose the absurd but constructive possibility that we are not alone for decision making in a multiverse as an individual person, but we seem to be entangled resulting in the possibility to initiate but also Veto an act which is even a base for Considering, Revolve, Meditate, or Ponder. Even Max Tegmark suggested already about the multiverse: “Is there a copy of you reading this article?” We could be instant entangled with at least one instant entangled anti-copy person living inside a Charge and Parity symmetric copy Universe. In that case we could construct a causal explanation for Libet’s strange results. New statistical difference research on RPI and RPII of repeated Libet experiments described here could support these ideas. Wikipedia says: “Democracy is a form of government in which all eligible citizens participate equally”. Free will in a multiverse seems to be based on: all entangled copy persons living in all CP symmetric copy universes, have the same possibility to Veto an act and participate equally.
see:
http://vixra.org/pdf/1401.0071v2.pdf
I was struck by sponsorship of your upcoming workshop by the templeton foundation. hope they don’t have one of their pets participating.
You guys might be interested my observation that look like a model of the particle in a box problem.
A pragmatic question. Since so far MWI has no new predictions compared to the original collapse model, how can one hope to convince the adepts of other “formulations”? If I believe in objective collapse, with all the extra postulates, or in Bohmian mechanics, with its pilot wave, why should I change my mind based on logic alone, in defiance of the scientific approach, where experiment is the ultimate arbiter?
Clearly simplicity alone is not good enough, since [SU(3)xSU(2)xU(1)x 3 generations x 20+ parameters x dark matter x dark energy x GR x initial conditions] is anything but simple. This rather complicated and incomplete model won over much simpler alternatives thanks to many extensive cycles of modeling, experimenting, observing and revising. Why should EQM be different?
“Common sense tells me that if A is observed happening twice as often as B, and if we are to believe in parallel universes, then there ought to be twice as many universes where A happens, or where A is seen to happen. But a detailed multiverse theory in which this is the case is hard to construct (Robin Hanson is one of the few to have tried).”
Let’s take the Schrodinger’s Cat case and postulate that usually the cat lives, but sometimes enough oxygen molecules tunnel their way out of the box so that the cat suffocates. Whether a specific O2 does or does not tunnel out of the box is a split, so there are many more universes in which the cat lives than those in which it dies, and the amplitudes measured over many such unethical experiments would be consistent with this.
Another case: a single electron is in an energy well. Sometimes (rarely) it bounces out of the well, but usually it does not. What if each different height it bounces is a split? Then again, there are many more universes in which it does not bounce high enough to get out than universes in which it does.
I just watched you on YouTube Sixty Symbols talking about the “embarrassment” that there’s no consensus about “meaning” of QM, although it works perfectly. I was wondering that since we (well, you professionals) seem to agree that some deeper theory is needed that will unite GR and QM, is it possible that it’s just too early to try to fully understand QM? Didn’t it take two hundred years to begin to understand Newton’s gravity? Could this be like Einstein’s futile attempt at unification before all the fields and particles were discovered?
I imagine this probably seems very naive, and that everyone has thought of this many times!
There are three questions I needed to address, but I was unable to add to my earlier comment about quantum recombination where for examples neutrons are split into separate state but then the state description is merged again into the original state.
So the first question is whether or not multiple worlds is at all reasonable, and it plainly isn’t. The whole problem with Everettian metaphysics is that it specifies an hierarchical tree ontology, whereas our friend mother nature prefers lattices. However my denouncement of Everettianism did not actually address the justification for Born’s hypothesis, which is two additional questions.
Traditional mathematics was very poor at describing an oriented surface. Not so when bivectors are introduced. A bivector is an oriented surface and belongs to a much improved conceptual algebra for describing physics, known as “Geometric Algebra”. In particular the treatment of rotations is vastly improved, and rotational kinematics. Think particle physics, think rotational dynamics. (Think Relativity, again think Lorentz boots which are rotations too).
Multiplication of bivectors is a natural operation, and leads to measures of magnitude that are geometric, and also meaningful. The Schwarz inequalities are fundamental properties of such spaces, and from there, a la Pythagorus, you get to natural definitions of magnitude. This is the domain where conserved quantities appear. As an example, angular momentum appears as an area in orbital theory, if you recall Keplers law. Equal areas traced in equal time. The mathematical-physical object behind it being a “rotor”.
It turns out that rotors tend to dominate all kinds of kinematical equations, which gives a direct dynamical link to the interpretation of bivector products, and their algebraic properties. You can spot that a mile away, when Planck’s constant appears, there is angular momentum along for the ride.
So there are two aspects to the Born rule. One is whether or observables would take the form of product. This has been strongly justified by for entirely algebraic reasons.
The second question is whither the observations arise, which is indeed a question of interpretation.
Initially Born in fact suggested the function without a square, until suggested the square as a footnote. Schrodinger guessed at his equations too, as did others. But the question would remain the same regardless of whether it was a cube or a fourth and a half power that worked in practice. But of course it is the square that works, and so the answer lies where it always has in physics, in the investigation of the mathematics and the foundations therein that lead to it being successful as applied to the model.
Geometric algebra is new, but already it has made dramatic simplifications in the way that the physical viewpoint is expressed, and real insights have been revealed. This is obviously the way forward. I doubt very much that new age psycho-science can contribute anything useful.