One of the most profound and mysterious principles in all of physics is the Born Rule, named after Max Born. In quantum mechanics, particles don’t have classical properties like “position” or “momentum”; rather, there is a wave function that assigns a (complex) number, called the “amplitude,” to each possible measurement outcome. The Born Rule is then very simple: it says that the probability of obtaining any possible measurement outcome is equal to the square of the corresponding amplitude. (The wave function is just the set of all the amplitudes.)
Born Rule: ![]()
The Born Rule is certainly correct, as far as all of our experimental efforts have been able to discern. But why? Born himself kind of stumbled onto his Rule. Here is an excerpt from his 1926 paper:
That’s right. Born’s paper was rejected at first, and when it was later accepted by another journal, he didn’t even get the Born Rule right. At first he said the probability was equal to the amplitude, and only in an added footnote did he correct it to being the amplitude squared. And a good thing, too, since amplitudes can be negative or even imaginary!
The status of the Born Rule depends greatly on one’s preferred formulation of quantum mechanics. When we teach quantum mechanics to undergraduate physics majors, we generally give them a list of postulates that goes something like this:
- Quantum states are represented by wave functions, which are vectors in a mathematical space called Hilbert space.
- Wave functions evolve in time according to the Schrödinger equation.
- The act of measuring a quantum system returns a number, known as the eigenvalue of the quantity being measured.
- The probability of getting any particular eigenvalue is equal to the square of the amplitude for that eigenvalue.
- After the measurement is performed, the wave function “collapses” to a new state in which the wave function is localized precisely on the observed eigenvalue (as opposed to being in a superposition of many different possibilities).
It’s an ungainly mess, we all agree. You see that the Born Rule is simply postulated right there, as #4. Perhaps we can do better.
Of course we can do better, since “textbook quantum mechanics” is an embarrassment. There are other formulations, and you know that my own favorite is Everettian (“Many-Worlds”) quantum mechanics. (I’m sorry I was too busy to contribute to the active comment thread on that post. On the other hand, a vanishingly small percentage of the 200+ comments actually addressed the point of the article, which was that the potential for many worlds is automatically there in the wave function no matter what formulation you favor. Everett simply takes them seriously, while alternatives need to go to extra efforts to erase them. As Ted Bunn argues, Everett is just “quantum mechanics,” while collapse formulations should be called “disappearing-worlds interpretations.”)
Like the textbook formulation, Everettian quantum mechanics also comes with a list of postulates. Here it is:
- Quantum states are represented by wave functions, which are vectors in a mathematical space called Hilbert space.
- Wave functions evolve in time according to the Schrödinger equation.
That’s it! Quite a bit simpler — and the two postulates are exactly the same as the first two of the textbook approach. Everett, in other words, is claiming that all the weird stuff about “measurement” and “wave function collapse” in the conventional way of thinking about quantum mechanics isn’t something we need to add on; it comes out automatically from the formalism.
The trickiest thing to extract from the formalism is the Born Rule. That’s what Charles (“Chip”) Sebens and I tackled in our recent paper:
Self-Locating Uncertainty and the Origin of Probability in Everettian Quantum Mechanics
Charles T. Sebens, Sean M. CarrollA longstanding issue in attempts to understand the Everett (Many-Worlds) approach to quantum mechanics is the origin of the Born rule: why is the probability given by the square of the amplitude? Following Vaidman, we note that observers are in a position of self-locating uncertainty during the period between the branches of the wave function splitting via decoherence and the observer registering the outcome of the measurement. In this period it is tempting to regard each branch as equiprobable, but we give new reasons why that would be inadvisable. Applying lessons from this analysis, we demonstrate (using arguments similar to those in Zurek’s envariance-based derivation) that the Born rule is the uniquely rational way of apportioning credence in Everettian quantum mechanics. In particular, we rely on a single key principle: changes purely to the environment do not affect the probabilities one ought to assign to measurement outcomes in a local subsystem. We arrive at a method for assigning probabilities in cases that involve both classical and quantum self-locating uncertainty. This method provides unique answers to quantum Sleeping Beauty problems, as well as a well-defined procedure for calculating probabilities in quantum cosmological multiverses with multiple similar observers.
Chip is a graduate student in the philosophy department at Michigan, which is great because this work lies squarely at the boundary of physics and philosophy. (I guess it is possible.) The paper itself leans more toward the philosophical side of things; if you are a physicist who just wants the equations, we have a shorter conference proceeding.
Before explaining what we did, let me first say a bit about why there’s a puzzle at all. Let’s think about the wave function for a spin, a spin-measuring apparatus, and an environment (the rest of the world). It might initially take the form
(α[up] + β[down] ; apparatus says “ready” ; environment0). (1)
This might look a little cryptic if you’re not used to it, but it’s not too hard to grasp the gist. The first slot refers to the spin. It is in a superposition of “up” and “down.” The Greek letters α and β are the amplitudes that specify the wave function for those two possibilities. The second slot refers to the apparatus just sitting there in its ready state, and the third slot likewise refers to the environment. By the Born Rule, when we make a measurement the probability of seeing spin-up is |α|2, while the probability for seeing spin-down is |β|2.
In Everettian quantum mechanics (EQM), wave functions never collapse. The one we’ve written will smoothly evolve into something that looks like this:
α([up] ; apparatus says “up” ; environment1)
+ β([down] ; apparatus says “down” ; environment2). (2)
This is an extremely simplified situation, of course, but it is meant to convey the basic appearance of two separate “worlds.” The wave function has split into branches that don’t ever talk to each other, because the two environment states are different and will stay that way. A state like this simply arises from normal Schrödinger evolution from the state we started with.
So here is the problem. After the splitting from (1) to (2), the wave function coefficients α and β just kind of go along for the ride. If you find yourself in the branch where the spin is up, your coefficient is α, but so what? How do you know what kind of coefficient is sitting outside the branch you are living on? All you know is that there was one branch and now there are two. If anything, shouldn’t we declare them to be equally likely (so-called “branch-counting”)? For that matter, in what sense are there probabilities at all? There was nothing stochastic or random about any of this process, the entire evolution was perfectly deterministic. It’s not right to say “Before the measurement, I didn’t know which branch I was going to end up on.” You know precisely that one copy of your future self will appear on each branch. Why in the world should we be talking about probabilities?
Note that the pressing question is not so much “Why is the probability given by the wave function squared, rather than the absolute value of the wave function, or the wave function to the fourth, or whatever?” as it is “Why is there a particular probability rule at all, since the theory is deterministic?” Indeed, once you accept that there should be some specific probability rule, it’s practically guaranteed to be the Born Rule. There is a result called Gleason’s Theorem, which says roughly that the Born Rule is the only consistent probability rule you can conceivably have that depends on the wave function alone. So the real question is not “Why squared?”, it’s “Whence probability?”
Of course, there are promising answers. Perhaps the most well-known is the approach developed by Deutsch and Wallace based on decision theory. There, the approach to probability is essentially operational: given the setup of Everettian quantum mechanics, how should a rational person behave, in terms of making bets and predicting experimental outcomes, etc.? They show that there is one unique answer, which is given by the Born Rule. In other words, the question “Whence probability?” is sidestepped by arguing that reasonable people in an Everettian universe will act as if there are probabilities that obey the Born Rule. Which may be good enough.
But it might not convince everyone, so there are alternatives. One of my favorites is Wojciech Zurek’s approach based on “envariance.” Rather than using words like “decision theory” and “rationality” that make physicists nervous, Zurek claims that the underlying symmetries of quantum mechanics pick out the Born Rule uniquely. It’s very pretty, and I encourage anyone who knows a little QM to have a look at Zurek’s paper. But it is subject to the criticism that it doesn’t really teach us anything that we didn’t already know from Gleason’s theorem. That is, Zurek gives us more reason to think that the Born Rule is uniquely preferred by quantum mechanics, but it doesn’t really help with the deeper question of why we should think of EQM as a theory of probabilities at all.
Here is where Chip and I try to contribute something. We use the idea of “self-locating uncertainty,” which has been much discussed in the philosophical literature, and has been applied to quantum mechanics by Lev Vaidman. Self-locating uncertainty occurs when you know that there multiple observers in the universe who find themselves in exactly the same conditions that you are in right now — but you don’t know which one of these observers you are. That can happen in “big universe” cosmology, where it leads to the measure problem. But it automatically happens in EQM, whether you like it or not.
Think of observing the spin of a particle, as in our example above. The steps are:
- Everything is in its starting state, before the measurement.
- The apparatus interacts with the system to be observed and becomes entangled. (“Pre-measurement.”)
- The apparatus becomes entangled with the environment, branching the wave function. (“Decoherence.”)
- The observer reads off the result of the measurement from the apparatus.
The point is that in between steps 3. and 4., the wave function of the universe has branched into two, but the observer doesn’t yet know which branch they are on. There are two copies of the observer that are in identical states, even though they’re part of different “worlds.” That’s the moment of self-locating uncertainty. Here it is in equations, although I don’t think it’s much help.
You might say “What if I am the apparatus myself?” That is, what if I observe the outcome directly, without any intermediating macroscopic equipment? Nice try, but no dice. That’s because decoherence happens incredibly quickly. Even if you take the extreme case where you look at the spin directly with your eyeball, the time it takes the state of your eye to decohere is about 10-21 seconds, whereas the timescales associated with the signal reaching your brain are measured in tens of milliseconds. Self-locating uncertainty is inevitable in Everettian quantum mechanics. In that sense, probability is inevitable, even though the theory is deterministic — in the phase of uncertainty, we need to assign probabilities to finding ourselves on different branches.
So what do we do about it? As I mentioned, there’s been a lot of work on how to deal with self-locating uncertainty, i.e. how to apportion credences (degrees of belief) to different possible locations for yourself in a big universe. One influential paper is by Adam Elga, and comes with the charming title of “Defeating Dr. Evil With Self-Locating Belief.” (Philosophers have more fun with their titles than physicists do.) Elga argues for a principle of Indifference: if there are truly multiple copies of you in the world, you should assume equal likelihood for being any one of them. Crucially, Elga doesn’t simply assert Indifference; he actually derives it, under a simple set of assumptions that would seem to be the kind of minimal principles of reasoning any rational person should be ready to use.
But there is a problem! Naïvely, applying Indifference to quantum mechanics just leads to branch-counting — if you assign equal probability to every possible appearance of equivalent observers, and there are two branches, each branch should get equal probability. But that’s a disaster; it says we should simply ignore the amplitudes entirely, rather than using the Born Rule. This bit of tension has led to some worry among philosophers who worry about such things.
Resolving this tension is perhaps the most useful thing Chip and I do in our paper. Rather than naïvely applying Indifference to quantum mechanics, we go back to the “simple assumptions” and try to derive it from scratch. We were able to pinpoint one hidden assumption that seems quite innocent, but actually does all the heavy lifting when it comes to quantum mechanics. We call it the “Epistemic Separability Principle,” or ESP for short. Here is the informal version (see paper for pedantic careful formulations):
ESP: The credence one should assign to being any one of several observers having identical experiences is independent of features of the environment that aren’t affecting the observers.
That is, the probabilities you assign to things happening in your lab, whatever they may be, should be exactly the same if we tweak the universe just a bit by moving around some rocks on a planet orbiting a star in the Andromeda galaxy. ESP simply asserts that our knowledge is separable: how we talk about what happens here is independent of what is happening far away. (Our system here can still be entangled with some system far away; under unitary evolution, changing that far-away system doesn’t change the entanglement.)
The ESP is quite a mild assumption, and to me it seems like a necessary part of being able to think of the universe as consisting of separate pieces. If you can’t assign credences locally without knowing about the state of the whole universe, there’s no real sense in which the rest of the world is really separate from you. It is certainly implicitly used by Elga (he assumes that credences are unchanged by some hidden person tossing a coin).
With this assumption in hand, we are able to demonstrate that Indifference does not apply to branching quantum worlds in a straightforward way. Indeed, we show that you should assign equal credences to two different branches if and only if the amplitudes for each branch are precisely equal! That’s because the proof of Indifference relies on shifting around different parts of the state of the universe and demanding that the answers to local questions not be altered; it turns out that this only works in quantum mechanics if the amplitudes are equal, which is certainly consistent with the Born Rule.
See the papers for the actual argument — it’s straightforward but a little tedious. The basic idea is that you set up a situation in which more than one quantum object is measured at the same time, and you ask what happens when you consider different objects to be “the system you will look at” versus “part of the environment.” If you want there to be a consistent way of assigning credences in all cases, you are led inevitably to equal probabilities when (and only when) the amplitudes are equal.
What if the amplitudes for the two branches are not equal? Here we can borrow some math from Zurek. (Indeed, our argument can be thought of as a love child of Vaidman and Zurek, with Elga as midwife.) In his envariance paper, Zurek shows how to start with a case of unequal amplitudes and reduce it to the case of many more branches with equal amplitudes. The number of these pseudo-branches you need is proportional to — wait for it — the square of the amplitude. Thus, you get out the full Born Rule, simply by demanding that we assign credences in situations of self-locating uncertainty in a way that is consistent with ESP.
We like this derivation in part because it treats probabilities as epistemic (statements about our knowledge of the world), not merely operational. Quantum probabilities are really credences — statements about the best degree of belief we can assign in conditions of uncertainty — rather than statements about truly stochastic dynamics or frequencies in the limit of an infinite number of outcomes. But these degrees of belief aren’t completely subjective in the conventional sense, either; there is a uniquely rational choice for how to assign them.
Working on this project has increased my own personal credence in the correctness of the Everett approach to quantum mechanics from “pretty high” to “extremely high indeed.” There are still puzzles to be worked out, no doubt, especially around the issues of exactly how and when branching happens, and how branching structures are best defined. (I’m off to a workshop next month to think about precisely these questions.) But these seem like relatively tractable technical challenges to me, rather than looming deal-breakers. EQM is an incredibly simple theory that (I can now argue in good faith) makes sense and fits the data. Now it’s just a matter of convincing the rest of the world!

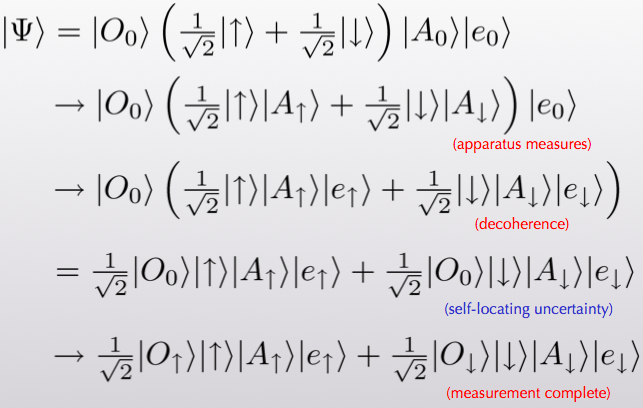
Sean,
Regarding Gleason, one thing I find a bit confusing (and I may just be misunderstanding your language) is your statement:
” There is a result called Gleason’s Theorem, which says roughly that the Born Rule is the only consistent probability rule you can conceivably have that depends on the wave function alone. So the real question is not “Why squared?”, it’s “Whence probability?” ”
Gleason’s Theorem depends on noncontextuality, which I argue follows from objectivism. But it does not simply follow “from the wavefunction alone”, in the usual sense of that phrase.
Perhaps when you say “depends on the wavefunction alone” you mean that the Born rule is the only measure that is based on objective features of the wavefunction, rather than emergent properties. However, then you say that the real problem is “whence probability?”.
The whole idea of the alternative measure (world-counting) is that it does generate, just like the Born rule, a consistent nontrivial probability measure (“nontrivial” meaning not always just 0 or 1). It just isn’t upheld by experiment. So the real problem can’t just be “whence probability?” That is also another “probability objection” to EQM that has been expressed — why should there be any nontrivial probabilities at all? — but this is an entirely different objection (and with much less substance, I think) than the Born rule objection.
Remember that in EQM we are allowed the wavefunction plus (for good reason) the idea of an observer with a memory, as an emergent property. Since a subjective view of probability sees nontrivial probabilities as inherently “emergent”, a subjectivist world-counting measure might still follow “from the wavefunction alone”, in the sense that is relevant here.
After all, there would not be a Born rule debate if Gleason proved it already from the wavefunction alone, since the claim of the objectors is exactly that no such proof has been produced, and that they have an alternative (nontrivial) measure.
Allan– I don’t necessarily disagree with your approach (“necessarily” inserted only because I won’t claim to have studied it carefully). There can be many different arguments to get the same right answer, and Chip and I are in favor of a plurality of approaches to deriving the Born Rule.
Having said that, I feel as if appeals to Gleason’s theorem aren’t addressing the actual worries that anti-Everettians have. The question really is primarily physical, rather than mathematical — everyone agrees that Gleason’s theorem is valid under the appropriate assumptions. Having interacted with well-informed and thoughtful anti-Everettians, it seems to me that their questions/objections tend to take forms like “Why shouldn’t I just count worlds?”, or “Why couldn’t I define arbitrary measures that are proportional to the number of descendants I have on each branch?”, or “Why should I think there is any uniquely-defined probability measure at all?”, or “Why shouldn’t my measure depend on what’s happening in other branches?”, or “Why are you even talking about probabilities when the theory is entirely deterministic?” These are all fundamentally physical/philosophical questions, not mathematical ones. So we tried to address them on their own terms, and we think that ESP is the kind of principle that most people would be willing to accept on basic physical grounds, independently of what theory we are working in.
For anyone who has alternative ways of deriving the Born Rule in EQM, our basic attitude is: great! I’m not sure how much is gained by looking for the “best” derivation. There are plenty of challenging questions about EQM beyond deriving the Born Rule, I’d rather think about those.
Hi Sean,
I don’t find much to outright disagree with there, but I guess I just prefer a different approach, going right back to the foundations of probability theory, rather than attempting to provide the “Born rule proof” that they are always asking for. But you are also right that the best approach is many approaches. And you are also right that the objectors themselves usually do ask for “physical relevance”, and there seems to be general agreement that the objection isn’t about the GNC. But I see this as a kind of trap. And by responding “in their own terms”, we fall right into it. No such proof will ever make them happy, since their objection is about “physical relevance”, which is purely intuitive and ill-defined, so the only way to respond “on their terms” is to make some assumptions about what is “physically relevant” that are as fuzzy as their request was to begin with. And since this is all fuzzy intuition, whatever principle you come up with, they will always be able to point out that you haven’t proved this principle, and since EQM claims to work from the formalism alone, you should be able to prove it.
This is the nature of the trap. There is something fishy going on here. They cannot have it both ways. We are either working purely formally, a la Everett’s postulates, or we are demanding physical relevance. You cannot demand both.
Assume, as you suggest, that the GNC is not fundamentally what is being objected to. This leaves us with something like the following.
Everettian: “Probability follows from the formalism alone.”
Objector: “No it doesn’t, because we could just count worlds.”
Everettian: “Not if GNC holds, and this is a very intuitive, reasonable, and clear assumption.”
Objector: “I agree it is acceptable so far as it goes. But it lacks physical relevance.”
Everettian: “So you agree that it is a reasonable assumption to make, in terms of acceptable measures on a vector space?”
Objector: “Yes, but I need physical relevance.”
Everettian: “But we are addressing what follows from the formalism alone — that is the whole idea here — so we are not concerned with physical relevance.”
Objector: “No, I need it.”
Everettian: “Ok, then, here is a version of GNC that has physical relevance. Look, I have applied the precise and analytically clear GNC to your fuzzy intuitive physical concepts and produced a version that, while lacking clarity and suffering from ambiguity, does indeed have physical relevance, and is still fairly simple.”
Objector: “But you haven’t proved it. You said that EQM could deliver probabilities from the formalism alone — that is the whole idea here — so you need to prove it.”
Everettian: “Then you object to the GNC? You want me to prove that?”
Objector: “No not at all, the GNC is fine. I just need you to add physical relevance.”
Everettian: “But you just said I had to prove it from the formalism alone!”
Objector: “Yes, but in a physically relevant way!”
Thus will they wiggle out of any argument you give them. Nothing short of a full explication of how conscious experience (and hence “physical intuition”) arises out of the interaction of subatomic particles will satisfy such a request — and I hope no one believes that that is a reasonable thing to ask of a physical theory.
In other worlds, either the real problem lies in the GNC, after all, or they are baiting you. I really do feel they need to be challenged more to defend world-counting (or whatever alternative they feel exists). I mean, really defend it, in terms of foundational principles of probability theory, not with weak and fuzzy hand-waving, or pleas of “Why can’t I just count worlds?”.
My answer to “Why can’t I just count worlds?” is “Go ahead, count worlds, but give me an argument for why worlds are the things that should count.”
Insisting on counting worlds is a little bit like counting colours in the typical probability problems we all remember from school. Take a bag with 10 marbles, 7 red and 3 blue. Pick one out at random. What is the probability that it is red? According to the world counters — “Why can’t I just count colours?” — the answer is 1/2. But of course the answer is really 7/10. This is because we count marbles, not colours. We count marbles categorized into colours. Categories are in the numerator, countable primitive objects are in the denominator. Colours are categories, not objective things like marbles (well, assume for now marbles are objective things!). So we count marbles, straight-out in the denominator, and categorized in the numerator by whatever category pleases us.
Worlds are categories, not things. Amplitudes are the things. This approach makes perfect sense in terms of a very basic high school conception of probability. What is the argument for counting worlds as things, given wavefunction realism? There may be one. But the objector needs to provide a systematic answer to this question if we are to consider their “objection” to be clearly stated. And it seems to me, that an argument of this nature will be an argument about the foundations of probability theory, and will have nothing whatever to do with quantum mechanics.
You didn’t address my question about possible convergence of different branches onto a common final state (e.g., in a “bouncing universe” scenario). I’d really be curious to hear your thoughts on that. My reason for asking, of course, is that if they can converge on a common final state then my understanding is we really have to say that both exist, in the same sense that we can’t say that the electron went through one slit or the other, but that both possibilities contributed. And that seems like a big problem for our intuitive sense that one possibility or another actually happened (which is not necessarily a problem for the physics, granted). But surely that is one motive for the non-Everett interpretations involving some sort of “wave function collapse” — to match our intuition that the outcome of the measurement happened and the other things didn’t happen, period. You can keep that intuition in the Everett interpretation at least for your own branch if the different possibilities never interfere in determining a common final state, but if they ever could converge on a common final state it means that intuition is just wrong. So I’d be very interested in your thoughts on whether the different branches can ever converge on the same final state. Thanks.
There is one thing I never quite understood about branching. If you have a singular wavefunction for the universe, then under whatever quantum theory completely describes all aspects of it, we should expect it to be a stationary state, with only the phase changing in time due to energy conservation. Any reduction of state along a branch would no longer be an eigenstate of the universal Hamiltonian. As a result, we would now have indeterminate total energy in that branch’s universe. I understand the ensemble of such branches would still resemble the original wavefunction, but every observer along a branch should be unable to determine the energy content of that universe. Determining the energy should in fact reverse every branching up until that point. How does this fit in with MWI?
Daniel,
Any interpretation of QM worth discussing should allow for a general-relativistic and second-quantized formulation. This means that it should never rely on concepts such as time, energy, particle, Hamiltonian, etc. Even the concept of “Schrodinger’s equation” should only be interpreted loosely, as “some differential equation linear in the state vector”, i.e. without assuming anything more about its structure or variables.
All these quantities appear only in approximations, when (or rather if) certain initial/boundary conditions are met. Most of them cannot even be defined at the fundamental level of the theory. So when discussing the interpretations of QM properly, you should try to rephrase your questions such that you don’t use these notions — otherwise they will only confuse you.
HTH, 🙂
Marko
Marko,
True, I’m considering a purely first quantization framework, which is not valid for a universal description. Nonetheless, ignore my use of energy to label eigenstates. The universal state description should still be a stationary state and if there is any state reduction along a branch, the reduction may not necessarily belong to the spectrum of the universe’s state operator. While a superposition of all branches would amount to such a valid state, each branch on its own would possibly encounter this problem. Another way to phrase it is that the branchings would define a basis that is not necessarily the pointer basis as defined by the universe’s (as in multiverse) state operator.
Unless the claim is that the multiverse is in some superposition of these pointer states, but intuitively I would think the actual state of the universe in a given world would determine this state from the beginning, that further interactions would not be needed to progressively branch the state into one deterministically evolving pointer state.
And again, I’m not trying to disprove MWI here via contrived counter example, I’m using this example to express a misunderstanding I’m having with MWI.
Dear Sean, i understand that the issue is not the ‘squaring’ but the origin of the probability. However, i was thinking if its reasonable to think that the origin of the squaring, hence the probability, is that squaring the wave function is measuring the area of some kind of a surface of sphere around the quantum system where the radius of the sphere is the amplitude, something like a holographic sheet that surrounds the quantum system under study which encodes the quantum information. So for spin states, we would have a sphere surface splitted into two parts (halves if the amplitudes are 1/sqrt(2) )where each part correspond to a state, the area of each part (normalised to the total surface area) is the probability of finding the system in that part. The (pi) would be not relevant here because normalisation deletes it and only the square of the amplitude stays. Does that make sense?
As if God playing dices was not bad enough now he must play dices and get all the numbers at each throw..
MWI and multiverse dont tell us much about reality but a lot about the ego of physicists that fell the need to imagine themselves in an infinite number of copies
The fact that you have to take squared modulus is due to the fact that we have arranged for the wave function to be linear. We didn’t need to do that. You can write QM in pure density matrix form and you will avoid the squared modulus. The pure density matrix is elegant in that it represents particles in terms of the relationship between where their initial and final state. It is an operator. In this form, the mathematics of QM is done with only one sort of object, the operator. The usual QM needs two objects, for example in finite problems, NxN operators and Nx1 states. In terms of QFT, pure density matrices correspond to propagators while states correspond to creation operators (kets) and annihilation operators (bras). One of the Landau and Lipshitz books mentions this correspondence in a footnote, IIRC, and Schwinger noted that you can define the creation and annihilation operators by taking one coordinate of a propagator (Green’s function) and setting it to a constant that he called the “fictitious vacuum”.
I’ve read over the paper more carefully now and the only question I have is, how are you justified in taking reduced density matrices without use of the Born Rule? You form the reduced density matrix in your derivation of the Born rule but a reduced density matrix is a partial trace. Specifically, it’s a full trace over one component of a separable Hilbert space, which means you’ve assumed the probability measure over the Hilbert space denoting the environment. Because of the decoherence condition, the system’s state is maximally entangled with that of the environment’s, so it’s no surprise that when you apply the Born Rule on the environment’s Hilbert Space, you get the same probabilities for the corresponding states of the system.
Am I missing something here? Is the reduced density matrix a justified construct when one does not have the Born Rule?
Daniel– “Constructing the reduced density matrix” is a purely mathematical process, completely well-posed whether or not you have the Born Rule. The question is what meaning we should attach to it, which is what our argument addresses. In Appendix B we address this in gruesome detail, and in the shorter paper we do the whole thing without ever using density matrices, just to assuage skepticism.
Of course, you do need to use the inner product on Hilbert space to construct the reduced density matrix. But the inner product is part of the theory, and nobody is going to make sense of quantum mechanics without assuming it.
Thank you for clarifying the goal of your derivation, Sean. The way I see it, deriving the Born rule in such a framework means showing it is the unique way to assign a probability measure to the Hilbert space of quantum mechanics. Perhaps it’s just lost on me, but I would think the Born rule is implicitly contained in the proposition that a Hilbert space describes quantum mechanical states (via Gleason’s theorem). It seems like this is an interpretation-independent result. I was viewing your method as an alternative to Gleason’s theorem here, but you’ve corrected me and said you’re looking to assign meaning to why Gleason’s theorem would hold, at least on an intuitive level.
I guess where I can’t take the leap is assuming that this way of counting the probability is the ontologically-entailed, unique method for correlating the elements of a Hilbert space with elements of reality even within an Everettian framework. I’m convinced it’s a consistent way of viewing quantum mechanics, but that’s about as far as I could go with this.
Daniel– As I said in the post, Gleason’s theorem (or Zurek’s envariance, or various applications of “frequency operators”) provides a good way to argue that “if you want to assign probabilities to branches of the wave function, Born’s Rule is the way to do it.” We view our contribution as explaining why assigning probabilities to branches of the wave function is a sensible thing to do. Namely, in EQM you deterministically evolve from perfect certainty to self-locating uncertainty, and once there you have a unique way of assigning credences that satisfies the ESP.
I think I’m seeing your point more clearly now. You agree that no matter the choice of heuristic tool you use to describe a Hilbert space, the Born rule is the probability measure that will result. So your goal is then to explain why Everettian quantum mechanics would have probabilities as elements of (or resulting from relationships among the elements of) its ontology. So I guess the question is if this is the unique framework for generating probability in a many worlds interpretation. Your assignments are unique within the framework, but I wonder if the framework itself is really the only way. An interesting read overall, thanks for engaging my curiosity.
Great, I think that puts us on the same page. We argue in the paper that Born probabilities follow uniquely from ESP, so if you believe ESP you don’t have much freedom. Of course you can choose to not accept ESP, then we can’t help you. We do argue against some naive versions of branch-counting, but in the end it’s a free country. (Personally if I have a set of simple assumptions that make predictions, and those predictions fit the data, I’m ready to move onto other questions.)
Out of curiosity though, why do you posit that each possible outcome is equally real? In philosophy, possible worlds are used as a way to posit counterfactual situations with the aid of modal logic. Why do these possible worlds not suffice, is it because it requires an additional explanation for why only one branch (or rather, set of observers along that branch) is privileged to be “real?” One could avoid such a question by relinquishing the assumption that reality is deterministic and instead argue that the determinism of quantum mechanics is the determinism of possibility, not necessity (referring to modal logic concepts of possibility and necessity here). Possibility is a weaker assumption than necessity after all.
Our attitude is that we take the theory at face value. According to EQM, there is a wave function that evolves unitarily, and it branches over time. Deciding that certain branches aren’t real seems like extra work that we see no reason to do. (That’s why Ted Bunn suggests that we refer to alternatives to EQM as “disappearing worlds interpretations.”)
I can see why such a view is attractive but I’d think positing that a statistical distribution is a real object belonging to the ontology of physics and not a device for organizing measured outcomes is a stronger assertion. It really depends on how you build up the quantum theory, how you describe it in the first place. I could take a unitarily evolving wavefunction and claim this represents a statistical distribution of possibilities.
In either case, the argument still has to be made why Newton’s laws (in the form of the galilei group) don’t act directly on the objects themselves, but on the distributions of measurements of these objects. It’s one thing to assert that the distribution is an ontological object, it’s another to reason it or derive it. A case could still be made that only on average do Newton’s laws hold on measurements and the distributions being held to such mechanics are a result of this constraint.
Interesting stuff to think about, I think I’m still an agnostic for now with regards to this issue.
I’ve been musing about the status of the wave function for the spin before measurement occurs in EQM. The premeasurement situation with the apparatus ready (environment 0) is the result of many past branchings. Therefore there are multiple different apparata in different “worlds.” Which apparatus (which world) will the wave function for the spin interact with? A reasonable answer is that it interacts only with apparata whose wave function evolved from the same environment (environment -1) that the spin state evolved from. But how are these interactions selected from all the other interactions that could occur?
I see a couple of possible resolutions.
1. The premeasurement wave function for the spin is not isolated. In fact it is entangled when it is created, with environment -1. It can’t become entangled with any other environment because of this preexisting linkage to the environment, so it won’t be measured by any apparatus except those that evolved from environment -1.
A criticism of approach (1) is that by the time the wave function for the spin reaches the apparatus, the apparatus and environment -1 have evolved to a multitude of new apparata and environments, none of which exactly matches environment -1 any longer. How could the measurement occur if we require preexisting coherence for there to be entanglement between apparatus and spin?
A potential answer to the criticism is that the premeasurement wave function for the spin is not entangled with all details of environment -1, only with its pointer states. As long as the pointer states of the apparatus in environment 0 remain coherent with those of environment -1, the measurement can occur.
2. In fact the spin function does interact with apparata in many different worlds. From the perspective of an apparatus, measurements occur continuously as it detects spin functions coming from different worlds (emitted by other (environment -1) states than the one that the apparatus evolved from). Is this consistent with observation? We do see quantum foam in experiments. Perhaps with proper accounting for conservation of energy, we could explain the virtual particles of quantum foam as a consequence of EQM.
I’m interested in your thoughts on the above. A one line answer “see chapter X of my book” would be fine if you’ve already treated this question somewhere. Thanks.
To toot my own horn a bit, as well as some other scholars’:
Eric Winsberg’s objection sounds similar to one raised independently by W. Zurek, A. Kent and myself, e.g. in
http://www.sciencedirect.com/science/article/pii/S1355219806000694
Sean C, I’ve really enjoyed following your work with Chip on this question. It’s a great paper you two have put together.