Hidden in my papers with Chip Sebens on Everettian quantum mechanics is a simple solution to a fun philosophical problem with potential implications for cosmology: the quantum version of the Sleeping Beauty Problem. It’s a classic example of self-locating uncertainty: knowing everything there is to know about the universe except where you are in it. (Skeptic’s Play beat me to the punch here, but here’s my own take.)
The setup for the traditional (non-quantum) problem is the following. Some experimental philosophers enlist the help of a subject, Sleeping Beauty. She will be put to sleep, and a coin is flipped. If it comes up heads, Beauty will be awoken on Monday and interviewed; then she will (voluntarily) have all her memories of being awakened wiped out, and be put to sleep again. Then she will be awakened again on Tuesday, and interviewed once again. If the coin came up tails, on the other hand, Beauty will only be awakened on Monday. Beauty herself is fully aware ahead of time of what the experimental protocol will be.
So in one possible world (heads) Beauty is awakened twice, in identical circumstances; in the other possible world (tails) she is only awakened once. Each time she is asked a question: “What is the probability you would assign that the coin came up tails?”
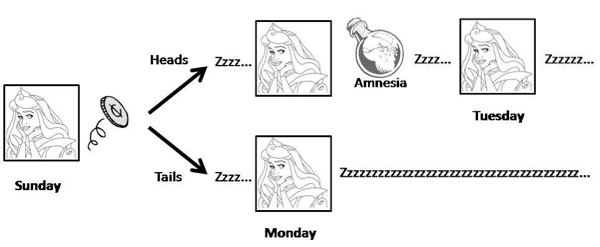
(Some other discussions switch the roles of heads and tails from my example.)
The Sleeping Beauty puzzle is still quite controversial. There are two answers one could imagine reasonably defending.
- “Halfer” — Before going to sleep, Beauty would have said that the probability of the coin coming up heads or tails would be one-half each. Beauty learns nothing upon waking up. She should assign a probability one-half to it having been tails.
- “Thirder” — If Beauty were told upon waking that the coin had come up heads, she would assign equal credence to it being Monday or Tuesday. But if she were told it was Monday, she would assign equal credence to the coin being heads or tails. The only consistent apportionment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.
The Sleeping Beauty puzzle has generated considerable interest. It’s exactly the kind of wacky thought experiment that philosophers just eat up. But it has also attracted attention from cosmologists of late, because of the measure problem in cosmology. In a multiverse, there are many classical spacetimes (analogous to the coin toss) and many observers in each spacetime (analogous to being awakened on multiple occasions). Really the SB puzzle is a test-bed for cases of “mixed” uncertainties from different sources.
Chip and I argue that if we adopt Everettian quantum mechanics (EQM) and our Epistemic Separability Principle (ESP), everything becomes crystal clear. A rare case where the quantum-mechanical version of a problem is actually easier than the classical version.
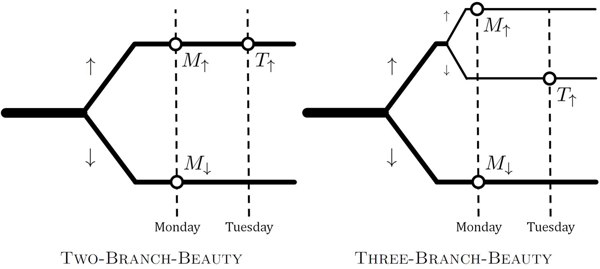
In the quantum version, we naturally replace the coin toss by the observation of a spin. If the spin is initially oriented along the x-axis, we have a 50/50 chance of observing it to be up or down along the z-axis. In EQM that’s because we split into two different branches of the wave function, with equal amplitudes.
Our derivation of the Born Rule is actually based on the idea of self-locating uncertainty, so adding a bit more to it is no problem at all. We show that, if you accept the ESP, you are immediately led to the “thirder” position, as originally advocated by Elga. Roughly speaking, in the quantum wave function Beauty is awakened three times, and all of them are on a completely equal footing, and should be assigned equal credences. The same logic that says that probabilities are proportional to the amplitudes squared also says you should be a thirder.
But! We can put a minor twist on the experiment. What if, instead of waking up Beauty twice when the spin is up, we instead observe another spin. If that second spin is also up, she is awakened on Monday, while if it is down, she is awakened on Tuesday. Again we ask what probability she would assign that the first spin was down.
This new version has three branches of the wave function instead of two, as illustrated in the figure. And now the three branches don’t have equal amplitudes; the bottom one is (1/√2), while the top two are each (1/√2)2 = 1/2. In this case the ESP simply recovers the Born Rule: the bottom branch has probability 1/2, while each of the top two have probability 1/4. And Beauty wakes up precisely once on each branch, so she should assign probability 1/2 to the initial spin being down. This gives some justification for the “halfer” position, at least in this slightly modified setup.
All very cute, but it does have direct implications for the measure problem in cosmology. Consider a multiverse with many branches of the cosmological wave function, and potentially many identical observers on each branch. Given that you are one of those observers, how do you assign probabilities to the different alternatives?
Simple. Each observer Oi appears on a branch with amplitude ψi, and every appearance gets assigned a Born-rule weight wi = |ψi|2. The ESP instructs us to assign a probability to each observer given by
![]()
It looks easy, but note that the formula is not trivial: the weights wi will not in general add up to one, since they might describe multiple observers on a single branch and perhaps even at different times. This analysis, we claim, defuses the “Born Rule crisis” pointed out by Don Page in the context of these cosmological spacetimes.
Sleeping Beauty, in other words, might turn out to be very useful in helping us understand the origin of the universe. Then again, plenty of people already think that the multiverse is just a fairy tale, so perhaps we shouldn’t be handing them ammunition.
Charlie, in your example you will be in room B 11/12 of the time and thus should bet accordingly. The example is not analogous as you waking up is not contingent on the outcome of the dice roll. You sample every possible outcome. The trick of this problem is that not every outcome is sampled.
Ignacio, the lesson I got from the Monty Hall problem was to be careful with how you define a state. The problem fools you because the “state” of having picked the wrong door is really 2 different states, despite them having the same qualitative description. In a problem of n-coin flips, it’s like specifying the state of k (k<n) heads. There's no single, unique realization of this description, the k heads can be distributed among the n (unique) coins in many possible ways. The doors are unique, that's the take-away, at least my take-away.
As for QM, like I said, I think Bertrand's paradox would be an interesting test for how robust the probability emergence is.
Daniel my takeaway of the monty hall problem is that for the analysis to be correct you have to assume that the game show host behaves predictably always in the same fashion, which is why he changes the probabilities. The game show host could not, say, choose to open the door to the car one time, or decline to open a door at all.
All of this enters into the analysis. But the point remains the same. You just have to be very careful about the rules of the game for any game of probability.
QM is based on probabilities and therein ends the relevance of this post.
Ignacio, I think it’s a valid interpretation, but I usually solve the problem by omitting the game show host as an agent and instead wrapping his actions up into the conditional probabilities. This comes down to state counting then and realizing that there are two different ways where you can switch to the door with the prize behind it. I’m sure modeling it as a two player game works too, but I think it’s really a one player game.
I would agree with you, except Sean’s construction of probabilities in MWI is not grounded in a normal probabilistic formulation of QM. It is possible that his interpretation is incorrect and will diverge from some probabilistic phenomena. I don’t believe his paper shows how his interpretation results in statements in QM that satisfy probability axioms, so there’s always a possibility.
OK, I see my mistake above. And clearly I jumped at the problem without reading Sean’s second scenario. It’s not trivial though counting possible outcomes and what’s sampled (at least not to me).
Daniel saying it is a one player game is by definition equivalent to saying that the game show host is a predictable automaton, not a free-will agent. An automaton with perfect knowledge of the answers.
There is a level of deception in thinking such puzzles can serve to explain fundamental rules of probability as applied in QM.
Ignacio, sure, but the point is you don’t have to include him in the analysis at all. You can just map his choices as outcomes and nothing is lost.
Obviously verifying that the interpretation produces the axioms of probability on its own would be enough. Don’t know why this isn’t standard protocol for interpretations to verify they satisfy the axioms of probability.
Doesn’t SB being told that “it’s Tuesday” mean she simply gets to rely on her memory of whether or not she was woken on Monday, since her memory was NOT washed of having been woken up on Monday?
If SB is at all relevant times fully informed about the rules that are in force, and then she’s woken on Tuesday and is TOLD, accurately and truthfully, “It’s Tuesday”, she simply needs rely to her own memory: if she does NOT remember on that Tuesday having been woken on the prior Monday, then necessarily, with 100% accuracy, she knows that the coin toss that occurred on Monday came up “Heads”. If she DOES remember on that Tuesday having been woken up the day before, then she knows that the coin toss that occurred on Monday came up “Tails”.
Similarly, if she’s told “It’s Monday”, what she does NOT know at that point is whether there’s still a plan in place to erase her memory; IOW she can’t know from just that information whether the coin of decision came up “Heads” or “Tails”. She’s thus compelled to rely on the honesty of the coin, so her accuracy, over enough experiments, is going to fall at or around 50:50.
If she’s not told what day it is, the condition of ‘knowing everything else’ is broken, because there are TWO pieces of information being kept from her: the outcome of the coin toss AND the day. And that’s where the ‘extra dimension of uncertainty’, the squaring of the uncertainty, kicks in.
“Before going to sleep, Beauty would have said that the probability of the coin coming up heads or tails would be one-half each.” — Well, that depends on whether she’s a Halfer or a Thirder.
Although I don’t mean that quite literally. Before going to sleep, Beauty will say that the probability of the coin coming up tails is 1/2, but the probability of her waking up to a world where it comes up tails will be 1/3. The fact that she “gets no new information” is a red herring; it would take new information to lead her to an opinion of 1/2 or 1. It also doesn’t matter that the coin needn’t be tossed till Monday night. When asked, she doesn’t know if it’s been tossed or not.
It’s interesting to think about what happens after the final interview. Suppose they don’t tell her what day it is, put her back to sleep, and awaken her on Wednesday (keeping her asleep through Tuesday if it came up Tails). In that case, Wednesday morning I claim she says the probability was 1/2.
Why not run the top course (heads) out to 99 awakenings. Now Sleeping Beauty can say with 99% certainty upon awakening that the coin came out heads. Heck, let’s dispense with this whole charade entirely and quietly kill her if it came out tails (with her prior consent and understanding, of course). Now Sleeping Beauty can say with 100% certainty that she cannot experience death from this experiment and is, in fact, immortal. But is it a quantum immortality?
This is all meant in good fun of course.
In the SB scenario the coin is only flipped once. There will be a 50-50 chance of it turning up either heads or tails. There can only be two outcomes regardless of what’s happening with Beauty.
If you are a “thirder” reconsider the possibilities again. If the coin flip is tales she will be interviewed on Monday only. There is a 50% chance that this will happen. If the coin flip lands on heads there would be a 50% chance that this will happen also; then she will be interviewed on both Monday and Tuesday, a requirement of the scenario. Beauty is awoken and interviewed no more than twice to make an assessment, in Sean’s scenario.
SB should realize that she cannot gain any knowledge at all during the experiment by its design and that a single coin flip, as in this scenario, can only have two outcomes of equal probability.
“As mentioned in the previous post, the fact that the amplitude gets squared to give you probabilities is pretty trivial. What’s non-trivial is explaining why there are probabilities at all.”
Oh, then I guess I’ve been misinterpreting this whole series. I thought the point of the paper and these posts was to derive the Born rule from a Many Worlds framework, not to explain why branching leads to apparent probabilities. Oops! (Many Worlds leading to probabilities already seems pretty straightforward to me. Though perhaps it’s not so straightforward to halfers.)
(To briefly follow up, I did see that the last post gave Gleason’s theorem as a justification for the Born rule. But I had thought that the rest of the post and paper were going to give another way to derive the Born rule that was not Gleason’s theorem. Perhaps this is why I’ve been so confused!)
The “thirder” argument may have its basis in the many-worlds interpretation, granted, but outside this interpretation I think it makes about as much sense as Schrödinger’s cat being alive, dead, or neither until it is observed, 3 possibilities 🙂
Just take an extreme case where SB is told she will be woken 100 times for Heads, but will not recall previous wakings. Then she can confidently say it is almost certainly Heads as I am sure I keep telling you! Forget 50/50
Amusing that I got 9 down-votes. Perhaps you all would like to play a little poker? A hint: if you can make money taking one side of a 50-50 bet, then it’s not a 50-50 bet. Anything more is overthinking the problem.
But if you do want to overthink it: the question is a conditional probability, what is the odds of heads GIVEN that SB has been wakened and asked the question. Now, does the latter constitute useful information? It obviously would if the conditions were that SB is not wakened at all on Tuesday, but here it is more subtle and I think that intuition can go either way. So we must look closely at the definition of probability: “that body of knowledge that is used to win money from the mathematically impaired.”
Joe, I have no idea why your answer has so many dislikes and mine has none when they essentially say the same thing, haha. I guess my initial calculation dissuaded users from reading past that point.
Thanks Daniel, also Ignacio. At the risk of belaboring the point: You are in a room. You are asked a question. You know that if you answer heads you will win the bet 2/3 of the time. If you answer tails you will win the bet 1/3 of the time. What are the odds that the answer is heads? (The fact that you might be asked the same question later, or before, is not relevant: your answer in either case has no effect on the subsequent offer).
p.s. I just noticed a typo in my previous comment: it should say “SB is not wakened at all on _tails_”
I think that one thing that is causing confusion with the bet is the idea that there is a secret double-payout in one case. But this is not true: each decision of SB controls only one payout. If the experiment is repeated 200 times, and SB always guesses heads, in the end she will have made 300 guesses and will have 300 betting slips, of which 200 say `heads, you win’ and 100 say `tails, you lose.’
I can only assume Joe got down-voted because he gave a disappontingly elementary derivation rather than applying a brane-world scenario. And using a monetary argument comes across as bragging about his his recently acquired wealth. 😉
edit: and if he’s not the real Joe Polchinski then certainly deserves the down votes!
As with many surveys, Sleeping Beauty’s answer will depend on how the question is phrased. If you say “I flipped a coin on Sunday; what was the probability that it came up heads?”, SB will answer “1/2.” That is because everyone, including SB, agrees that P(H) = 1/2.
On the other hand, if you say “I flipped a coin on Sunday; what is the probability that it came up heads?”, SB will answer “2/3”. That is because poor SB cannot observe the act of flipping the coin, even accounting for the fact that the outcome is masked. She can only observe the fact of having been woken. And everyone, including SB, agrees that P(W and H) = 2/3.
Sleeping Beauty, then, belongs to a fairly extensive class of popular philosophical “problems”, such as Monty Hall, “why does a mirror reverse left and right but not up and down”, and the Two Envelopes problem which are not problems at all because when specified with sufficient precision, they have correct answers.
It is therefore tempting to roll ones’ eyes in these cases, and certainly that is a reasonable reaction to some particular arguments. But I have to say that I found working through the permutations of the Two Envelopes problem required to eliminate contradictions to be quite stimulating; and no doubt many people feel the same about their own pet favorites.
I think it is interesting that by coincidence, Sabine Hossenfelder has just posted a physical and mathematical perspective on another of these philosophical “problems”: can you touch your nose?
Phil Koop
“Why does a mirror reverse left and right but not up and down?” I’m surprised that is considered a philosophical problem – the (quite well-known) explanation is that the mirror just relects what’s facing it, so if you turn (yourself or an object) around a vertical axis to face it you reverse left and right, and if you turn around a horizontal axis to face it you reverse up and down. (Or write on a thin piece of paper, and hold it with the writing facing a light, then what you see through the back of the paper is what you see in a mirror reflection)
Joe I think the real source of the confusion in this sort of situations is believing that your intuition is an automatically good description of the probabilities.
For the Monty Hall problem the intuition is that you stand nothing to gain by switching doors and in a real game show that is probably correct because the host would just as often try to trick you. In this instance the problem is the thinking that the coin was tossed and it is either heads or tails so 50/50 has to be the answer.
It is nothing complicated just a tendency in the human mind.
I didn’t really care for the explanation of the Monty Hall problem either, that you would increase your odds to 50/50 for switching doors after a loser one was revealed. It didn’t seem like it would be truly 50/50 if you decided to simply take the same action every time. Your intuition would tell you that it would still just be 1/3, but it will just be one out of the three that you didn’t pick to begin with.
I think the Sleeping Beauty problem is a lot easier than that. If you had a 1/2 chance of it her not being woken up on Monday from the original coin flip and a 1/4 chance of being woke on Monday or Tuesday, then that would add up to 100%.
1/4 + 1/4 +1/2 = 4/4 = 100%
It would be more like the question, “What are the odds of getting heads twice in a row?” The only thing is that, if you fail to get heads, you stop flipping the coin. If you flip the coin twice there are only 4 possible outcomes, it is just that some of the outcomes are not realized, because there would be no point of trying again if you already failed. Then you would have a 50% chance of failing on the first try, so half of the time Sleeping Beauty would just sleep through the whole ordeal. Then there would only be 1/4 chance that she was woken on Monday, since there was also a 1/2 chance that the coin was flipped again making it Tuesday due to her amnesia.
I think it would go along more with what happens in everyday experience. It could mean the difference of rather everyone that goes to Vegas in the multiverse comes out a winner, or if mostly everyone that goes to Vegas is a loser. The odds are always stacked in the houses favor. Then mostly everyone always losses everything. Although, if there was an equal chance to win as there was to lose, then in the multiverse someone would always come out a winner. Then people always come back as a loser every time no matter how many times they vacation to Vegas. If every possibility in the multiverse was realized, then it would seem like if you gambled enough that anyone could eventually become a winner!