Thanksgiving

This year we give thanks for a technique that is central to both physics and mathematics: the Fourier transform. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, and Landauer’s Principle.)

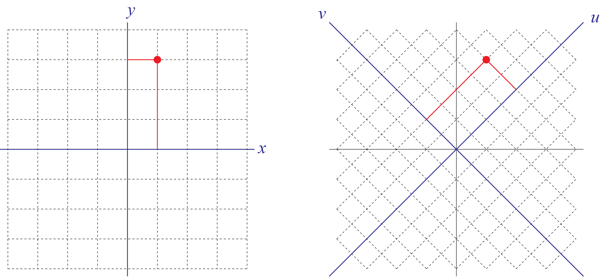
Let’s say you want to locate a point in space — for simplicity, on a two-dimensional plane. You could choose a coordinate system (x, y), and then specify the values of those coordinates to pick out your point: (x, y) = (1, 3).

But someone else might want to locate the same point, but they want to use a different coordinate system. That’s fine; points are real, but coordinate systems are just convenient fictions. So your friend uses coordinates (u, v) instead of (x, y). Fortunately, you know the relationship between the two systems: in this case, it’s u = y+x, v = y-x. The new coordinates are rotated (and scaled) with respect to the old ones, and now the point is represented as (u, v) = (4, 2).

Fourier transforms are just a fancy version of changes of coordinates. The difference is that, instead of coordinates on a two-dimensional space, we’re talking about coordinates on an infinite-dimensional space: the space of all functions. (And for technical reasons, Fourier transforms naturally live in the world of complex functions, where the value of the function at any point is a complex number.)

Think of it this way. To specify some function f(x), we give the value of the function f for every value of the variable x. In principle, an infinite number of numbers. But deep down, it’s not that different from giving the location of our point in the plane, which was just two numbers. We can certainly imagine taking the information contained in f(x) and expressing it in a different way, by “rotating the axes.”

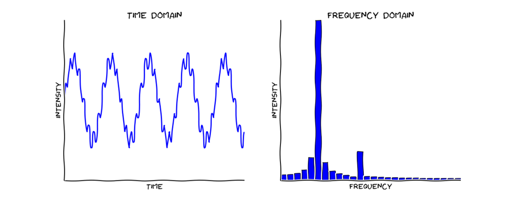
That’s what a Fourier transform is. It’s a way of specifying a function that, instead of telling you the value of the function at each point, tells you the amount of variation at each wavelength. Just as we have a formula for switching between (u, v) and (x, y), there are formulas for switching between a function f(x) and its Fourier transform f(ω):

.

Absorbing those formulas isn’t necessary to get the basic idea. If the function itself looks like a sine wave, it has a specific wavelength, and the Fourier transform is just a delta function (infinity at that particular wavelength, zero everywhere else). If the function is periodic but a bit more complicated, it might have just a few Fourier components.

In general, the Fourier transform f(ω) gives you “the amount of the original function that is periodic with period 2πω.” This is sometimes called the “frequency domain,” since there are obvious applications to signal processing, where we might want to take a signal that has an intensity that varies with time and pick out the relative strength of different frequencies. (Your eyes and ears do this automatically, when they decompose light into colors and sound into pitches. They’re just taking Fourier transforms.) Frequency, of course, is the inverse of wavelength, so it’s equally good to think of the Fourier transform as describing the “length domain.” A cosmologist who studies the large-scale distribution of galaxies will naturally take the Fourier transform of their positions to construct the power spectrum, revealing how much structure there is at different scales.

To my (biased) way of thinking, where Fourier transforms really come into their own is in quantum field theory. QFT tells us that the world is fundamentally made of waves, not particles, and it is extremely convenient to think about those waves by taking their Fourier transforms. (It is literally one of the first things one is told to do in any introduction to QFT.)

But it’s not just convenient, it’s a worldview-changing move. One way of characterizing Ken Wilson’s momentous achievement is to say “physics is organized by length scale.” Phenomena at high masses or energies are associated with short wavelengths, where our low-energy long-wavelength instruments cannot probe. (We need giant machines like the Large Hadron Collider to create high energies, because what we are really curious about are short distances.) But we can construct a perfectly good effective theory of just the wavelengths longer than a certain size — whatever size it is that our theoretical picture can describe. As physics progresses, we bring smaller and smaller length scales under the umbrella of our understanding.

Without Fourier transforms, this entire way of thinking would be inaccessible. We should be very thankful for them — as long as we use them wisely.

Note that Joseph Fourier, inventor of the transform, is not the same as Charles Fourier, utopian philosopher. Joseph, in addition to his work in math and physics, invented the idea of the greenhouse effect. Sadly that’s not something we should be thankful for right now.