General relativity is a rich theory that makes a wide variety of experimental predictions. It’s been tested many ways, and always seems to pass with flying colors. But there’s always the possibility that a different test in a new regime will reveal some anomalous behavior, which would open the door to a revolution in our understanding of gravity. (I didn’t say it was a likely possibility, but you don’t know until you try.)
Not every experiment tests different things; sometimes one set of observations is done with a novel technique, but is actually just re-examining a physical regime that has already been well-explored. So it’s interesting to have a handle on what regimes we have already tested. For GR, that’s not such an easy question; it’s difficult to compare tests like gravitational redshift, the binary pulsar, and Big Bang nucleosynthesis.
So it’s good to see a new paper that at least takes a stab at putting it all together:
Linking Tests of Gravity On All Scales: from the Strong-Field Regime to Cosmology
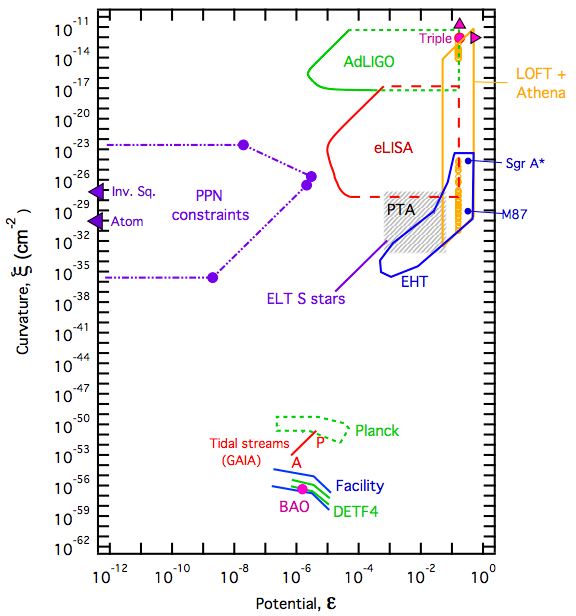
Tessa Baker, Dimitrios Psaltis, Constantinos SkordisThe current effort to test General Relativity employs multiple disparate formalisms for different observables, obscuring the relations between laboratory, astrophysical and cosmological constraints. To remedy this situation, we develop a parameter space for comparing tests of gravity on all scales in the universe. In particular, we present new methods for linking cosmological large-scale structure, the Cosmic Microwave Background and gravitational waves with classic PPN tests of gravity. Diagrams of this gravitational parameter space reveal a noticeable untested regime. The untested window, which separates small-scale systems from the troubled cosmological regime, could potentially hide the onset of corrections to General Relativity.
The idea is to find a simple way of characterizing different tests of GR so that they can be directly compared. This will always be something of an art as well as a science — the metric tensor has ten independent parameters (six of which are physical, given four coordinates we can choose), and there are a lot of ways they can combine together, so there’s little hope of a parameterization that is both easy to grasp and covers all bases.
Still, you can make some reasonable assumptions and see whether you make progress. Baker et al. have defined two parameters: the “Potential” ε, which roughly tells you how deep the gravitational well is, and the “Curvature” ξ, which tells you how strongly the field is changing through space. Again — these are reasonable things to look at, but not really comprehensive. Nevertheless, you can make a nice plot that shows where different experimental constraints lie in your new parameter space.
The nice thing is that there’s a lot of parameter space that is unexplored! You can think of this plot as a finding chart for experimenters who want to dream up new ways to test our best understanding of gravity in new regimes.
One caveat: it would be extremely surprising indeed if gravity didn’t conform to GR in these regimes. The philosophy of effective field theory gives us a very definite expectation for where our theories should break down: on length scales shorter than where we have tested the theory. It would be weird, although certainly not impossible, for a theory of gravity to work with exquisite precision in our Solar System, but break down on the scales of galaxies or cosmology. It’s not impossible, but that fact should weigh heavily in one’s personal Bayesian priors for finding new physics in this kind of regime. Just another way that Nature makes life challenging for we poor human physicists.
Richard Benish:
In your comment and from your website writings you suggest that the interior of a ball of matter would be a new and interesting place to look for deviations from usual gravity. As you say, a test particle placed in a hole thru the diameter of a sphere of uniform density is expected to oscillate back and forth thru the center like a harmonic oscillator. The restoring acceleration =(4/3)pi G rho r (proportional to r as it should be for a simple harmonic oscillator). I think you have been considering solid mass densities rho> 1 g/cm3. Another interesting region might be gas (like STP He rho=1.79e-4 g/cm) for which the restoring acceleration is 5.0e-9 cm/sec2 per meter of displacement.
So, consider a 1 meter radius balloon of STP He in orbit around the earth. The starting acceleration for a test particle (inside the balloon at r=1 m) by Newton would be 5.0e-9 cm/sec2 toward the center of the sphere with a 10 day period of oscillation. This may be compared to the acceleration of the universe’s expansion by Dark Energy, the Hubble acceleration, and the MOND acceleration a0:
5.0e-9 cm/sec2 inward acceleration of STP He at r=1 meter
~e-33 cm/sec2 outward acceleration of DE density at r=1 m … too small to notice in osc period
7.0e-8 cm/sec2 outward Hubble acceleration … might stop osc since it’s greater than He inward accel
1.2e-8 cm/sec2 inward acceleration of MOND … would drastically shorten osc period
Neither DE, Hubble, or MOND is actually expected to affect experiments near the earth, but as you say this would be a new experimental region to look at.
JohnB: it was david calling people names. What you’re describing is SR time dilation, as per the simple inference of time dilation due to relative velocity. There’s no problem with that. Looking again at your “doesn’t work out” comment, IMHO that’s because you’re looking at it back to front. An optical clock goes slower when its lower because light goes slower when its lower, because a concentration of energy in the guise of a star “conditions” the surrounding space altering its properties, this effect diminishing with distance. We call it gravitational time dilation, but gravity is there because the speed of light varies, not the other way round. Only you never measure the local speed of light to be any different because of the wave nature of matter, see this.
The “simple inference of time dilation due to relative velocity” is wrong. The equation produced by that derivation is the inverse of the function of time. Even in the paper you linked, equation 13 shows that;
t = … = … = t’/(sqrt(1 – v^2 / c^2)
That would equal;
t’ = t sqrt(1 – v^2 / c^2)
The equation derived in the simple inference of time dilation is the inverse of that, because the variables have been switched.
t’ = t/(sqrt(1 – v^2 / c^2)
In the simple inference equation, you would actually get a larger dilated time. More ticks of the clock would mean that more time has passed by. That would be because t’ was assigned to the hypotenuse of the triangle that is the larger side. More distance to cover would mean that more time would be needed. Then that equation would actually say that time speeds up as an object approaches the speed of light.
I had a read a couple of books saying that no one could find the right way to solve the light clock problem. Then it is still used to teach first year physics students anyways. When I was taught this equation in school, we where told that it doesn’t come to the correct answer, but we use it anyways because the correct equation was too hard to derive. Then the derivation of this doesn’t have to be that difficult…
John, you’ve misunderstood it. It’s very simple, it’s just Pythagoras’s theorem. The hypotenuse is the light path, the base is your speed as a fraction of c, the height gives the Lorentz factor, then there’s a reciprocal to distinguish time dilation from length contraction. The t’ is given by the number of reflections, when the light moves like this /\/\/\ there’s fewer of them.
Quick grammar correction:
The last sentence should be …”for US poor human physicists.” The word WE is the subject of a verb, whereas US is an object of one.
Just one more part of humanity that TOEs have yet to explain.
@JohnD
What a coincidence, then you would have to take the inverse of time to then find the number of ticks on the clock to get a similar final answer from this “frequency”. The problem with that theory is that both observers do not measure the same speed of light. The observer in constant motion would not measure the light ray traveling at an angle with their dilated time to get the correct speed of light. Then the relativistic effect is just an illusion and doesn’t say light travels the same speed all the way through, while my derivation says it is a property of spacetime itself. Then the speed of light is constant from the beginning.
Then it would have the advantage of the distance ” ct ” to actually be the distance light would travel at a constant speed. An observer at rest will never measure ” ct’ ” with their own clock. If they did, they would get a different value for the speed of light. Time dilation is real, and it has to be in order for the speed of light to be the same constant throughout the derivation.
It’s not a mechanical fallacy. It is an aspect of time itself, “t”. Simple geometry doesn’t lie.
John B,
Have a look at http://arxiv.org/abs/1111.6986
which is the first quantum mechanical treatment of Shapiro delay I have seen.
Also besides photons, Shapiro delay is also experienced by neutrinos(which we know
from SN1987A) and gravitational waves (in other words gravity gravitates)
Shantanu