Algebra of the Infrared

In my senior year of college, when I was beginning to think seriously about graduate school, a magical article appeared in the New York Times magazine. Called “A Theory of Everything,” by KC Cole, it conveyed the immense excitement that had built in the theoretical physics community behind an idea that had suddenly exploded in popularity after burbling beneath the surface for a number of years: a little thing called “superstring theory.” The human-interest hook for the story was simple — work on string theory was being led by a brilliant 36-year-old genius, a guy named Ed Witten. It was enough to cement Princeton as the place I most wanted to go to for graduate school. (In the end, they didn’t let me in.)

Nearly thirty years later, Witten is still going strong. As evidence, check out this paper that recently appeared on the arxiv, with co-authors Davide Gaiotto and Greg Moore:

Algebra of the Infrared: String Field Theoretic Structures in Massive N=(2,2) Field Theory In Two Dimensions
Davide Gaiotto, Gregory W. Moore, Edward Witten

We introduce a “web-based formalism” for describing the category of half-supersymmetric boundary conditions in 1+1 dimensional massive field theories with N=(2,2) supersymmetry and unbroken U(1)R symmetry. We show that the category can be completely constructed from data available in the far infrared, namely, the vacua, the central charges of soliton sectors, and the spaces of soliton states on ℝ, together with certain “interaction and boundary emission amplitudes”. These amplitudes are shown to satisfy a system of algebraic constraints related to the theory of A∞ and L∞ algebras. The web-based formalism also gives a method of finding the BPS states for the theory on a half-line and on an interval. We investigate half-supersymmetric interfaces between theories and show that they have, in a certain sense, an associative “operator product.” We derive a categorification of wall-crossing formulae. The example of Landau-Ginzburg theories is described in depth drawing on ideas from Morse theory, and its interpretation in terms of supersymmetric quantum mechanics. In this context we show that the web-based category is equivalent to a version of the Fukaya-Seidel A∞-category associated to a holomorphic Lefschetz fibration, and we describe unusual local operators that appear in massive Landau-Ginzburg theories. We indicate potential applications to the theory of surface defects in theories of class S and to the gauge-theoretic approach to knot homology.

I cannot, in good conscience, say that I understand very much about this new paper. It’s a kind of mathematica/formal field theory that is pretty far outside my bailiwick. (This is why scientists roll their eyes when a movie “physicist” is able to invent a unified field theory, build a time machine, and construct nanobots that can cure cancer. Specialization is real, folks!)

But there are two things about the paper that I nevertheless can’t help but remarking on. One is that it’s 429 pages long. I mean, damn. That’s a book, not a paper. Scuttlebutt informs me that the authors had to negotiate specially with the arxiv administrators just to upload the beast. Most amusingly, they knew perfectly well that a 400+ page work might come across as a little intimidating, so they wrote a summary paper!

An Introduction To The Web-Based Formalism
Davide Gaiotto, Gregory W. Moore, Edward Witten

This paper summarizes our rather lengthy paper, “Algebra of the Infrared: String Field Theoretic Structures in Massive N=(2,2) Field Theory In Two Dimensions,” and is meant to be an informal, yet detailed, introduction and summary of that larger work.

This short, user-friendly introduction is a mere 45 pages — still longer than 95% of the papers in this field. After a one-paragraph introduction, the first words of the lighthearted summary paper are “Let X be a Kähler manifold, and W : X → C a holomorphic Morse function.” So maybe it’s not that informal.

The second remarkable thing is — hey look, there’s my name! Both of the papers cite one of my old works from when I was a grad student, with Simeon Hellerman and Mark Trodden. (A related paper was written near the same time by Gary Gibbons and Paul Townsend.)

Domain Wall Junctions are 1/4-BPS States
Sean M. Carroll, Simeon Hellerman, Mark Trodden

We study N=1 SUSY theories in four dimensions with multiple discrete vacua, which admit solitonic solutions describing segments of domain walls meeting at one-dimensional junctions. We show that there exist solutions preserving one quarter of the underlying supersymmetry — a single Hermitian supercharge. We derive a BPS bound for the masses of these solutions and construct a solution explicitly in a special case. The relevance to the confining phase of N=1 SUSY Yang-Mills and the M-theory/SYM relationship is discussed.

Simeon, who was a graduate student at UCSB at the time and is now faculty at the Kavli IPMU in Japan, was the driving force behind this paper. Mark and I had recently written a paper on different ways that topological defects could intersect and join together. Simeon, who is an expert in supersymmetry, noticed that there was a natural way to make something like that happen in supersymmetric theories: in particular, you could have domain walls (sheets that stretch through space, separating different possible vacuum states) could intersect at “junctions.” Even better, domain-wall junction configurations would break some of the supersymmetry but not all of it. Setups like that are known as BPS states, and are highly valued and useful to supersymmetry aficionados. In general, solutions to quantum field theories are very difficult to find and characterize with any precision, but the BPS property lets you invoke some of the magic of supersymmetry to prove results that would otherwise be intractable.

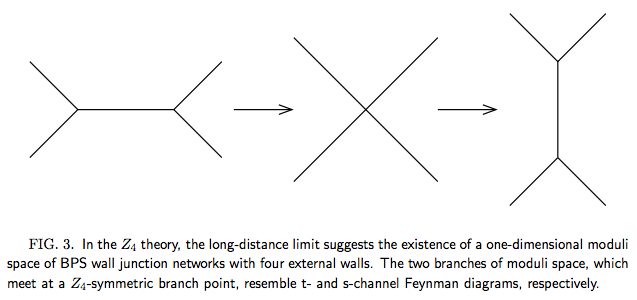
Admittedly, the above paragraph is likely to be just as opaque to the person on the street as the Gaiotto/Moore/Witten paper is to me. The point is that we were able to study the behavior of domain walls and how they come together using some simple but elegant techniques in field theory. Think of drawing some configuration of walls as a network of lines in a plane. (All of the configurations we studied were invariant along some “vertical” direction in space, as well as static in time, so all the action happens in a two-dimensional plane.) Then we were able to investigate the set of all possible ways such walls could come together to form allowed solutions. Here’s an example, using walls that separate four different possible vacuum states:

As far as I understand it (remember — not that far!), this is a very baby version of what Gaiotto, Moore, and Witten have done. Like us, they look at a large-distance limit, worrying about how defects come together rather than the detailed profiles of the individual configurations. That’s the “infrared” in their title. Unlike us, they go way farther, down a road known as “categorification” of the solutions. In particular, they use a famous property of BPS states: you can multiply them together to get other BPS states. That’s the “algebra” of their title. To mathematicians, algebras aren’t just ways of “solving for x” in equations that tortured you in high school; they are mathematical structures describing sets of vectors that can be multiplied by each other to produce other vectors. (Complex numbers are an algebra; so are ordinary three-dimensional vectors, using the cross product operation.)

At this point you’re allowed to ask: Why should I care? At least, why should I imagine putting in the work to read a 429-page opus about this stuff? For that matter, why did these smart guys put in the work to write such an opus?

It’s a reasonable question, but there’s also a reasonable answer. In theoretical physics there are a number of puzzles and unanswered questions that we are faced with, from “Why is the mass of the Higgs 125 GeV?” to “How does information escape from black holes?” Really these are all different sub-questions of the big one, “How does Nature work?” By construction, we don’t know the answer to these questions — if we did, we’d move onto other ones. But we don’t even know the right way to go about getting the answers. When Einstein started thinking about fitting gravity into the framework of special relativity, Riemannian geometry was absolutely the last thing on his mind. It’s hard to tell what paths you’ll have to walk down to get to the final answer.

So there are different techniques. Some people will try a direct approach: if you want to know how information comes out of a black hole, think as hard as you can about what happens when black holes radiate. If you want to know why the Higgs mass is what it is, think as hard as you can about the Higgs field and other possible fields we haven’t yet found.

But there’s also a more patient, foundational approach. Quantum field theory is hard; to be honest, we don’t understand it all that well. There’s little question that there’s a lot to be learned by studying the fundamental behavior of quantum field theories in highly idealized contexts, if only to better understand the space of things that can possibly happen with an eye to eventually applying them to the real world. That, I suspect, is the kind of motivation behind a massive undertaking like this. I don’t want to speak for the authors; maybe they just thought the math was cool and had fun learning about these highly unrealistic (but still extremely rich) toy models. But the ultimate goal is to learn some basic wisdom that we will someday put to use in answering that underlying question: How does Nature work?

As I said, it’s not really my bag. I don’t have nearly the patience nor that mathematical aptitude that is required to make real progress in this kind of way. I’d rather try to work out on general principles what could have happened near the Big Bang, or how our classical world emerges out of the quantum wave function.

But, let a thousand flowers bloom! Gaiotto, Moore, and Witten certainly know what they’re doing, and hardly need to look for my approval. It’s one strategy among many, and as a community we’re smart enough to probe in a number of different directions. Hopefully this approach will revolutionize our understanding of quantum field theory — and at my retirement party everyone will be asking me why I didn’t stick to working on domain-wall junctions.