Math

Sir Michael Atiyah, one of the world’s greatest living mathematicians, has proposed a derivation of α, the fine-structure constant of quantum electrodynamics. A preprint is here. The math here is not my forte, but from the theoretical-physics point of view, this seems misguided to me.

(He’s also proposed a proof of the Riemann conjecture, I have zero insight to give there.)

Caveat: Michael Atiyah is a smart cookie and has accomplished way more than I ever will. It’s certainly possible that, despite the considerations I mention here, he’s somehow onto something, and if so I’ll join in the general celebration. But I honestly think what I’m saying here is on the right track.

In quantum electrodynamics (QED), α tells us the strength of the electromagnetic interaction. Numerically it’s approximately 1/137. If it were larger, electromagnetism would be stronger, atoms would be smaller, etc; and inversely if it were smaller. It’s the number that tells us the overall strength of QED interactions between electrons and photons, as calculated by diagrams like these.
As Atiyah notes, in some sense α is a fundamental dimensionless numerical quantity like e or π. As such it is tempting to try to “derive” its value from some deeper principles. Arthur Eddington famously tried to derive exactly 1/137, but failed; Atiyah cites him approvingly.

But to a modern physicist, this seems like a misguided quest. First, because renormalization theory teaches us that α isn’t really a number at all; it’s a function. In particular, it’s a function of the total amount of momentum involved in the interaction you are considering. Essentially, the strength of electromagnetism is slightly different for processes happening at different energies. Atiyah isn’t even trying to derive a function, just a number.

This is basically the objection given by Sabine Hossenfelder. But to be as charitable as possible, I don’t think it’s absolutely a knock-down objection. There is a limit we can take as the momentum goes to zero, at which point α is a single number. Atiyah mentions nothing about this, which should give us skepticism that he’s on the right track, but it’s conceivable.

More importantly, I think, is the fact that α isn’t really fundamental at all. The Feynman diagrams we drew above are the simple ones, but to any given process there are also much more complicated ones, e.g.

And in fact, the total answer we get depends not only on the properties of electrons and photons, but on all of the other particles that could appear as virtual particles in these complicated diagrams. So what you and I measure as the fine-structure constant actually depends on things like the mass of the top quark and the coupling of the Higgs boson. Again, nowhere to be found in Atiyah’s paper.

Most importantly, in my mind, is that not only is α not fundamental, QED itself is not fundamental. It’s possible that the strong, weak, and electromagnetic forces are combined into some Grand Unified theory, but we honestly don’t know at this point. However, we do know, thanks to Weinberg and Salam, that the weak and electromagnetic forces are unified into the electroweak theory. In QED, α is related to the “elementary electric charge” e by the simple formula α = e²/4π. (I’ve set annoying things like Planck’s constant and the speed of light equal to one. And note that this e has nothing to do with the base of natural logarithms, e = 2.71828.) So if you’re “deriving” α, you’re really deriving e.

But e is absolutely not fundamental. In the electroweak theory, we have two coupling constants, g and g’ (for “weak isospin” and “weak hypercharge,” if you must know). There is also a “weak mixing angle” or “Weinberg angle” θ_W relating how the original gauge bosons get projected onto the photon and W/Z bosons after spontaneous symmetry breaking. In terms of these, we have a formula for the elementary electric charge: e = g sinθ_W. The elementary electric charge isn’t one of the basic ingredients of nature; it’s just something we observe fairly directly at low energies, after a bunch of complicated stuff happens at higher energies.

Not a whit of this appears in Atiyah’s paper. Indeed, as far as I can tell, there’s nothing in there about electromagnetism or QED; it just seems to be a way to calculate a number that is close enough to the measured value of α that he could plausibly claim it’s exactly right. (Though skepticism has been raised by people trying to reproduce his numerical result.) I couldn’t see any physical motivation for the fine-structure constant to have this particular value

These are not arguments why Atiyah’s particular derivation is wrong; they’re arguments why no such derivation should ever be possible. α isn’t the kind of thing for which we should expect to be able to derive a fundamental formula, it’s a messy low-energy manifestation of a lot of complicated inputs. It would be like trying to derive a fundamental formula for the average temperature in Los Angeles.

Again, I could be wrong about this. It’s possible that, despite all the reasons why we should expect α to be a messy combination of many different inputs, some mathematically elegant formula is secretly behind it all. But knowing what we know now, I wouldn’t bet on it.

This year we give thanks for an area of mathematics that has become completely indispensable to modern theoretical physics: Riemannian Geometry. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, and the Fourier Transform. Ten years of giving thanks!)

Now, the thing everyone has been giving thanks for over the last few days is Albert Einstein’s general theory of relativity, which by some measures was introduced to the world exactly one hundred years ago yesterday. But we don’t want to be everybody, and besides we’re a day late. So it makes sense to honor the epochal advance in mathematics that directly enabled Einstein’s epochal advance in our understanding of spacetime.

Highly popularized accounts of the history of non-Euclidean geometry often give short shrift to Riemann, for reasons I don’t quite understand. You know the basic story: Euclid showed that geometry could be axiomatized on the basis of a few simple postulates, but one of them (the infamous Fifth Postulate) seemed just a bit less natural than the others. That’s the parallel postulate, which has been employed by generations of high-school geometry teachers to torture their students by challenging them to “prove” it. (Mine did, anyway.)

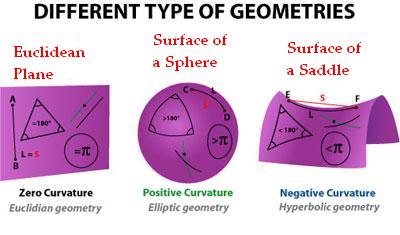
It can’t be proved, and indeed it’s not even necessarily true. In the ordinary flat geometry of a tabletop, initially parallel lines remain parallel forever, and Euclidean geometry is the name of the game. But we can imagine surfaces on which initially parallel lines diverge, such as a saddle, or ones on which they begin to come together, such as a sphere. In those contexts it is appropriate to replace the parallel postulate with something else, and we end up with non-Euclidean geometry.

Historically, this was first carried out by Hungarian mathematician János Bolyai and the Russian mathematician Nikolai Lobachevsky, both of whom developed the hyperbolic (saddle-shaped) form of the alternative theory. Actually, while Bolyai and Lobachevsky were the first to publish, much of the theory had previously been worked out by the great Carl Friedrich Gauss, who was an incredibly influential mathematician but not very good about getting his results into print.

The new geometry developed by Bolyai and Lobachevsky described what we would now call “spaces of constant negative curvature.” Such a space is curved, but in precisely the same way at every point; there is no difference between what’s happening at one point in the space and what’s happening anywhere else, just as had been the case for Euclid’s tabletop geometry.

Real geometries, as takes only a moment to visualize, can be a lot more complicated than that. Surfaces or solids can twist and turn in all sorts of ways. Gauss thought about how to deal with this problem, and came up with some techniques that could characterize a two-dimensional curved surface embedded in a three-dimensional Euclidean space. Which is pretty great, but falls far short of the full generality that mathematicians are known to crave.

Fortunately Gauss had a brilliant and accomplished apprentice: his student Bernard Riemann. (Riemann was supposed to be studying theology, but he became entranced by one of Gauss’s lectures, and never looked back.) In 1853, Riemann was coming up for Habilitation, a German degree that is even higher than the Ph.D. He suggested a number of possible dissertation topics to his advisor Gauss, who (so the story goes) chose the one that Riemann thought was the most boring: the foundations of geometry. The next year, he presented his paper, “On the hypotheses which underlie geometry,” which laid out what we now call Riemannian geometry.

With this one paper on a subject he professed not to be all that interested in, Riemann (who also made incredible contributions to analysis and number theory) provided everything you need to understand the geometry of a space of arbitrary numbers of dimensions, with an arbitrary amount of curvature at any point in the space. It was as if Bolyai and Lobachevsky had invented the abacus, Gauss came up with the pocket calculator, and Riemann had turned around a built a powerful supercomputer.

Like many great works of mathematics, a lot of new superstructure had to be built up along the way. A subtle but brilliant part of Riemann’s work is that he didn’t start with a larger space (like the three-dimensional almost-Euclidean world around us) and imagine smaller spaces embedded with it. Rather, he considered the intrinsic geometry of a space, or how it would look “from the inside,” whether or not there was any larger space at all.

Next, Riemann needed a tool to handle a simple but frustrating fact of life: “curvature” is not a single number, but a way of characterizing many questions one could possibly ask about the geometry of a space. What you need, really, are tensors, which gather a set of numbers together in one elegant mathematical package. Tensor analysis as such didn’t really exist at the time, not being fully developed until 1890, but Riemann was able to use some bits and pieces of the theory that had been developed by Gauss.

Finally and most importantly, Riemann grasped that all the facts about the geometry of a space could be encoded in a simple quantity: the distance along any curve we might want to draw through the space. He showed how that distance could be written in terms of a special tensor, called the metric. You give me segment along a curve inside the space you’re interested in, the metric lets me calculate how long it is. This simple object, Riemann showed, could ultimately be used to answer any query you might have about the shape of a space — the length of curves, of course, but also the area of surfaces and volume of regions, the shortest-distance path between two fixed points, where you go if you keep marching “forward” in the space, the sum of the angles inside a triangle, and so on.

Unfortunately, the geometric information implied by the metric is only revealed when you follow how the metric changes along a curve or on some surface. What Riemann wanted was a single tensor that would tell you everything you needed to know about the curvature at each point in its own right, without having to consider curves or surfaces. So he showed how that could be done, by taking appropriate derivatives of the metric, giving us what we now call the Riemann curvature tensor. Here is the formula for it:

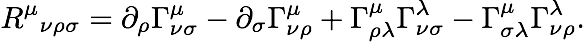
This isn’t the place to explain the whole thing, but I can recommend some spiffy lecture notes, including a very short version, or the longer and sexier textbook. From this he deduced several interesting features about curvature. For example, the intrinsic curvature of a one-dimensional space (a line or curve) is alway precisely zero. Its extrinsic curvature — how it is embedded in some larger space — can be complicated, but to a tiny one-dimensional being, all spaces have the same geometry. For two-dimensional spaces there is a single function that characterizes the curvature at each point; in three dimensions you need six numbers, in four you need twenty, and it goes up from there.

There were more developments in store for Riemannian geometry, of course, associated with names that are attached to various tensors and related symbols: Christoffel, Ricci, Levi-Civita, Cartan. But to a remarkable degree, when Albert Einstein needed the right mathematics to describe his new idea of dynamical spacetime, Riemann had bequeathed it to him in a plug-and-play form. Add the word “time” everywhere we’ve said “space,” introduce some annoying minus signs because time and space really aren’t precisely equivalent, and otherwise the geometry that Riemann invented is the same we use today to describe how the universe works.

Riemann died of tuberculosis before he reached the age of forty. He didn’t do bad for such a young guy; you know you’ve made it when you not only have a Wikipedia page for yourself, but a separate (long) Wikipedia page for the list of things named after you. We can all be thankful that Riemann’s genius allowed him to grasp the tricky geometry of curved spaces several decades before Einstein would put it to use in the most beautiful physical theory ever invented.

This year we give thanks for a technique that is central to both physics and mathematics: the Fourier transform. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, and Landauer’s Principle.)

Let’s say you want to locate a point in space — for simplicity, on a two-dimensional plane. You could choose a coordinate system (x, y), and then specify the values of those coordinates to pick out your point: (x, y) = (1, 3).

But someone else might want to locate the same point, but they want to use a different coordinate system. That’s fine; points are real, but coordinate systems are just convenient fictions. So your friend uses coordinates (u, v) instead of (x, y). Fortunately, you know the relationship between the two systems: in this case, it’s u = y+x, v = y-x. The new coordinates are rotated (and scaled) with respect to the old ones, and now the point is represented as (u, v) = (4, 2).

Fourier transforms are just a fancy version of changes of coordinates. The difference is that, instead of coordinates on a two-dimensional space, we’re talking about coordinates on an infinite-dimensional space: the space of all functions. (And for technical reasons, Fourier transforms naturally live in the world of complex functions, where the value of the function at any point is a complex number.)

Think of it this way. To specify some function f(x), we give the value of the function f for every value of the variable x. In principle, an infinite number of numbers. But deep down, it’s not that different from giving the location of our point in the plane, which was just two numbers. We can certainly imagine taking the information contained in f(x) and expressing it in a different way, by “rotating the axes.”

That’s what a Fourier transform is. It’s a way of specifying a function that, instead of telling you the value of the function at each point, tells you the amount of variation at each wavelength. Just as we have a formula for switching between (u, v) and (x, y), there are formulas for switching between a function f(x) and its Fourier transform f(ω):

.

Absorbing those formulas isn’t necessary to get the basic idea. If the function itself looks like a sine wave, it has a specific wavelength, and the Fourier transform is just a delta function (infinity at that particular wavelength, zero everywhere else). If the function is periodic but a bit more complicated, it might have just a few Fourier components.

In general, the Fourier transform f(ω) gives you “the amount of the original function that is periodic with period 2πω.” This is sometimes called the “frequency domain,” since there are obvious applications to signal processing, where we might want to take a signal that has an intensity that varies with time and pick out the relative strength of different frequencies. (Your eyes and ears do this automatically, when they decompose light into colors and sound into pitches. They’re just taking Fourier transforms.) Frequency, of course, is the inverse of wavelength, so it’s equally good to think of the Fourier transform as describing the “length domain.” A cosmologist who studies the large-scale distribution of galaxies will naturally take the Fourier transform of their positions to construct the power spectrum, revealing how much structure there is at different scales.

To my (biased) way of thinking, where Fourier transforms really come into their own is in quantum field theory. QFT tells us that the world is fundamentally made of waves, not particles, and it is extremely convenient to think about those waves by taking their Fourier transforms. (It is literally one of the first things one is told to do in any introduction to QFT.)

But it’s not just convenient, it’s a worldview-changing move. One way of characterizing Ken Wilson’s momentous achievement is to say “physics is organized by length scale.” Phenomena at high masses or energies are associated with short wavelengths, where our low-energy long-wavelength instruments cannot probe. (We need giant machines like the Large Hadron Collider to create high energies, because what we are really curious about are short distances.) But we can construct a perfectly good effective theory of just the wavelengths longer than a certain size — whatever size it is that our theoretical picture can describe. As physics progresses, we bring smaller and smaller length scales under the umbrella of our understanding.

Without Fourier transforms, this entire way of thinking would be inaccessible. We should be very thankful for them — as long as we use them wisely.

Note that Joseph Fourier, inventor of the transform, is not the same as Charles Fourier, utopian philosopher. Joseph, in addition to his work in math and physics, invented the idea of the greenhouse effect. Sadly that’s not something we should be thankful for right now.