String theory, the current leading candidate for a theory of quantum gravity as well as other particles and forces, doesn't connect directly to the world we see. It's possible that there is a large landscape of possible states of theory, with the hope that one of them represents our universe. The existence of a landscape implies the existence of a corresponding swampland -- universes that are not compatible with string theory. I talk with Cumrun Vafa, a respected physicist and originator of the swampland program, about how we might use constraints on what kinds of physics are compatible with string theory to make predictions about cosmology and other experimental regimes.
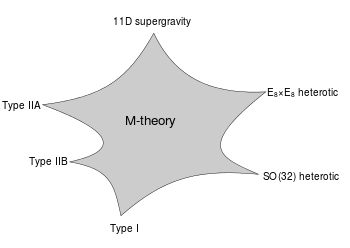
Here is a research paper on Swampland phenomenology. In the conversation we refer to a famous diagram representing different ten-dimensional string theories, as well as 11-dimensional M-theory, as different limits of an underlying fundamental theory. Here is the diagram:
Support Mindscape on Patreon.
Cumrun Vafa received his Ph.D. in physics from Princeton University. He is currently Hollis Professor of Mathematicks and Natural Philosophy, and Chair of the Physics Department, at Harvard University. He has done fundamental work on the dynamics of superstrings, the entropy of black holes, F-theory, and other topics. Among his awards are the Breakthrough Prize in Fundamental Physics, the Dirac Medal, and the Dannie Heineman Prize for Mathematical Physics. He is a member of the American Academy of Arts and Sciences and the National Academy of Sciences. He is the author of the book Puzzles to Unravel the Universe.
0:00:00.5 Sean Carroll: Hello everyone. Welcome to the Mindscape Podcast. I'm your host, Sean Carroll. Those of you who were old enough, are old enough to have been paying attention to physics blogs and magazines and books in the early part of the 21st century, in the 2000s, might remember the string wars, there was a slightly public debate about the status of string theory. One of the most popular ways of trying to get a quantum theory of gravity. String theory was born in the late '60s, early '70s, nobody paid any attention to it, became hugely popular suddenly in the 1980s when John Schwartz and Michael Green showed that certain flaws that it might have, and that many theories do have, string theory did not have the anomalies canceled, is the short version. That was the first super string revolution. Then there's a second super string revolution in the '90s where Paul Shensky and Whitney and other people used D-branes and non-perturbative things to say that there were dualities that united all the string theories.
0:01:02.3 SC: Very exciting once again. But 10 years after that, by the mid 2000s, there was a backlash. And people like Lee Smolin, former Mindscape guest, Peter White and other people, wrote books and talked a lot on the internet about how string theory was not really physics. It was not successful as physics anyway. There were no predictions. There never would be predictions, et cetera. This backlash had essentially no impact on physics research. It didn't affect who got hired by physics departments or what research people were doing or anything like that, but it had a huge impact on public perception. So much so that I was communicating, I forget exactly why, with a editor from new scientist back in 2007, and I mentioned string theory, the most popular theory of quantum gravity, et cetera. And they said, wait, people still do string theory in 2007.
0:02:01.1 SC: And I said, yes, it's actually still quite popular in leading physics departments around the world. So I ended up writing an article for new scientists about how string theory is not dead yet, and I explained that I'm not a string theorist. This should not be my job. But anyway, still not dead, almost 20 years after that. However, it is absolutely fair to say that it can be frustrating to try to figure out this theory that is extremely rich in its structure and its content and has led to all sorts of provocative ideas like holography and AdS/CFT and all these things, but still hasn't really made a prediction for an experiment that you could go and directly test what is the status of it. If you go back to the interview I did with Brian Green on Mindscape some time ago, Brian, a very effective, very influential string theorist, was very honest that maybe will just end up being math and not really be supported by physics departments after all.
0:03:04.8 SC: Or maybe today's podcast episode will change your mind about that. So we're very happy to have Cumrun Vafa, who is one of the leading string theorists of the world, department chair of physics at Harvard. And as you'll find out, he has natural philosophy in his job title, which I was very pleased to learn. And Cumrun has done many very important things in the history of string theory. He worked with, again, former Mindscape guest, Andrew Strominger, to count the microscopic states in certain kinds of black holes and show that you get the entropy right from a string theory perspective, et cetera. But for a while now, for almost 20 years, he has been pursuing what is called the Swampland Program. You may have heard of the string theory landscape, the idea, there's many different theories that you could get at low energies in the late universe by compactifying extra dimensions in string theory.
0:03:54.0 SC: What the Swampland Program proposes, is that there are many theories that you cannot get by starting with string theory and compactifying it. And so there's so many that you can, it seems like a lot. But the argument is that there's even many, many, many, many more, infinitely many more that you cannot get. Those are the Swampland theories. So there are certain, in other words, constraints on observable low energy physics, that you naturally get from demanding that the low energy physics you get, be part of a more fully complete theory of quantum gravity, namely string theory. And so that may be true, but how useful is it? And I knew about the Swampland Program for a while now, and I was sort of following from afar. It tried to make some statements about cosmology and about particle physics and things like that.
0:04:48.4 SC: You have to be careful. You don't want your beautiful theory of everything to already be ruled out, but you do want it to be ruled out of a bull, right? You want it to be falsifiable if it can be. So that's a fine line to walk, but ultimately the theory decides what it is, not we human beings. So in the episode today, I clearly have not been following well enough because I learned a lot, about the Swampland Program, and in particular, a very specific set of ideas that come out of it about dark matter and dark energy and how that fits in with particle physics and so forth. Clearly, very speculative conjectural. Don't get too excited. But the reason why I even mention it here in the intro is that it clearly disproves the idea that 20 years ago, string theory was dead, that you couldn't connect it to observations, that there's no possible way of doing that.
0:05:43.1 SC: You just, it's true that we didn't have very careful, specific guidance from observations, but we had to think more carefully about the theory and maybe what we're talking about in today's episode will lead to direct confrontation between the string theory and experiment. Maybe it won't, maybe it will all go away. That's the nature of physics. We have to do the work, and then we will find out whether it fits or not. But first, you gotta do the work. So that's a good lesson to learn whether or not this particular theory ends up being the right theory of gravity and cosmology and so forth. Occasional reminder, you're allowed to support the Mindscape podcast by going to patreon.com/seanmcarroll, kicking in a buck or two per episode, and you get ad free versions of the podcast, plus the ability to ask, ask me anything questions, and very, very supportive. Let me just give a shout out to all the Patreon supporters. I enormously appreciate your support. It very much keeps me going here at Mindscape. So with that, let's go.
[music]
0:07:02.0 SC: Cumrun Vafa, welcome to the Mindscape Podcast.
0:07:03.5 Cumrun Vafa: Thank you. Thank you Sean for having me. It's great to be here and talk with you about science.
0:07:08.5 SC: The first question I have to ask is that, is it in fact true that you are a professor of natural philosophy?
0:07:16.0 CV: Professor of mathematics and natural philosophy, hardest professor of mathematics and natural philosophy? That's what it is. This is oldest chair in science in the United States. It was given to Harvard, gifted to Harvard by Hollis, I think it was 1726, the last year that Newton lived. Wow. So Newton was still alive where presumably where this was gifted. And the terms of the chair says nothing about teaching Newtonian mechanics, surprisingly. He talks about other kinds of physics, but not Newton. So it surprised me to see that.
0:07:57.0 SC: That was too cutting edge at the time. Probably, but I don't if you know but I am also a professor of natural philosophy that is my title at Johns Hopkins.
0:08:05.6 CV: Oh, wow.
0:08:05.8 SC: But unlike yours, mine is only a year and a half old, not many hundreds of years old, so.
0:08:10.9 CV: Oh, I see. And the probably yours does not have any funny spelling, like my mathematics, where it has a K.
0:08:16.3 SC: That's right. We spell mathematics correctly here. [laughter] Okay. So let's just dive in to the idea of string theory. String theory is obviously, I'm sure everyone in the audience has heard of it. Probably 85% of them have strong opinions about it one way or the other. And they probably know that it involves replacing particles with little strings. But why don't you give us the sales pitch for what makes string theory different from other attempts to quantize gravity? We hear claims about how string theory is the most promising theory of quantum gravity we have. Where did that originally come from, that feeling?
0:08:56.8 CV: So the problem has been when you take gravity and quantize that with the usual rules of particle physics, you get nonsensical answers when you try to compute physical processes using it. So the physical processes are organized in terms of the degree of approximation or what we call the loop expansion. And the higher and higher degrees that you go, the more and more divergent things you get in quantum gravity and things all look good if you just view it as particle physics kind of technology. And so if you view gravity as a particle, and we call it graviton that does not seem to work. So string theories claim to fame or why we think is an exciting theory is that when you try to study just vibrating strengths, relativistic vibrating strengths, basically means that these guys go with the speed of light air and they have properties which are respect relativity.
0:10:08.4 CV: Then you amazingly find that among these excitations, the light excitations and the masses excitation includes graviton along with these other excitations, which correspond to higher oscillating modes of string, which are more massive. So you get a tower of particles, the light cell, which is gravity. Now the surprise was that when you try to compute these corrections to physical processes, you find that what used to be infinite suddenly becomes finite. And that was remarkable because it wasn't put in by hand that somehow magically it becomes finite and the physical aptitudes and processes we compute become well-defined. And this was kind of a shock because you, first of all, we were not trying, by we, I mean the people who originally thought of strength theory, they were not trying to describe gravity. Gravity was an afterthought. They noticed that they have some particle, which is mass that has the same spin as graviton, and they later identified it with graviton and somehow without putting it by hand, it gave you that.
0:11:17.9 CV: And then the physical processes, which they competed became finite automatically in this theory. And it had very different symmetries than the particle physics did. So there, it used some stringy symmetry. So I will try to explain one example of what this stringy symmetry is that particle physics doesn't see. So string, imagine string like a little loo, p like a circle. And imagine this loop going around and coming back to itself. So if you look at what the loop spans, it looks this loop as it string the circle as it goes around, spans the donut, what we call the Taurus.
0:11:55.3 SC: Yeah.
0:11:55.6 CV: Now there are two sides to it. One is the cross-sectional side, which is the string itself, and then the other one is the path it went through the other circles. So there are two circles involved, and the size of these two circles can be different, and you can choose different sizes. Now, one of the symmetries of the string is that, well, actually you can revert to which one is the string and which one is the path you are going through. In other words, you could view the other one as a string and the path going around as a cross-sectional path versus the other one. And so in this way, you revert the roles of these two radii. And this kind of symmetry, which is manifest in the picture I just told you, is absent in the particle physics kind of situation. And this is one of the main reasons you get finiteness in the string theory amplitude. So it is a key fact, that is a one dimensional object or a high dimensional object for this to come out. So we see that it cannot, could not have been done in the context of just graviton viewed as particles.
0:12:52.1 CV: So this was the origin of why string theory became popular in terms of studying as a candidate for quantum gravity. And there has been a huge amount of things that we have learned about string theory, which is not just about quantum gravity, it's about also quantum field theory about various properties or other things that we didn't expect. And it has enhanced our understanding of not just quantum gravity, but of all physics dualities that we have discovered and all that that we can talk about. They're all kind of enrich our understanding of broader meaning of what the consistent physical theory is.
0:13:26.6 SC: And so when people say, I just wanna make sure that we're separating out the sort of careful claims from the short little mottos, when people say string theory is a finite theory of gravity, is that a 100% established or is that within a certain regime, or do we even know what string theory is, deep down?
0:13:49.5 CV: So there are different amounts of establishment. First of all, at the level of computing perturbation theory, which means these order by order corrections, it has been established as finite. Okay. So there at least we know it's finite in that sense. Now there's also a process where you can go beyond these corrections one by one and see the whole thing. There's a whole thing finite or not. Given that the first one is finite, we think the other one should also be finite. So that one is not proven. Though there are symmetries that I alluded to, which maps this problem to another one, which been in some sense, no it's finite. And in those cases we can say, at least in this example, we know that particular string theory is finite, even beyond an approximation scheme that we computed. So the option of the answer to your question is that depends on exact details of what we know, but we have enough evidence to believe it is finite.
0:14:42.4 SC: But I do hear that people still ask themselves the question, what is string theory?
0:14:48.8 CV: Yes. What is string theory is not an easy question to answer precisely because of the following. What we learned about string theory, and I think this is probably the most important discovery of string theory, is the discovery of duality symmetries. Duality symmetry basically is telling you that the fundamental description of a theory is ambiguous. That if somebody told you that this theory is made of X or Y or Z ingredients, then they have by definition picked the particular vantage point, which is not the food theory. So when we say a theory is a theory about strings, we have also taken that vantage point of something. So then the question becomes, what is this bigger thing that includes all of these things without referring to any specific one? And that's naturally much harder to define because we get our understanding by going to corners and by corners of parameter space.
0:15:44.5 CV: That's what I mean. You choose some particular parameters where strings emerges as objects that you can actually study. That means they're basically you can think about the most classical objects that you can view them and evolve them and study them. This happens only in specific corners. The totality of what is possible includes also places where this cannot be done. So therefore when we say what is string theory, we should clearly not refer only to these particular corners where some particular structures emerge. But the bigger picture of what this whole thing is none.: And this whole thing does not just include one dimensional loops of energy, which we call strings. It could have other corners where you have higher dimensional objects, for example, being relevant for the discussions. And so this mishmash of objects, which we can morph from one to the other, as you go from one parameter corner to the other, it's called the duality symmetry in string theory. And this is precisely why it's post exciting and also very hard to define what do you mean by string theory?
0:16:45.0 SC: Good. So I have a way of thinking about dualities and I'm not sure if I'm right, so I'm gonna run it by you and tell me if I'm on the right track. I think of dualities as when you have a single quantum theory that has multiple different classical limits or maybe multiple different classical theories you could quantize to get that single quantum theory. Is that how string theorists think about it?
0:17:10.0 CV: Kind of, yes. So in other words, you have multiple limits, which classical picture emerges. Exactly. But those are only corners for us. And that bigger collection of thing that's the middle thing is the bulk of it, I would say. So those limits are only our approximation schemes allow you to say something, but the bulk of it is middle and that one, we don't have a good say of what it is that we are talking about. And that's the main question.
0:17:34.0 SC: Yeah. Okay, good. So moving gradually in the direction of the real world, the most famous thing about string theory is that it seems to want to live in 10 dimensional space time. And I do not live in 10 dimensional space time. So somehow you need to hide the extra dimensions. Is that still how people think about it?
0:17:53.5 CV: Yeah. So when you say you don't live in 10 dimensional space time, what you really, I think, probably are alluding to is that the space that you can see with your eyes, three dimensional and the time that you experience is only one dimensional, and that's your four dimensional space time. It does not mean that there are no other dimensions because you may not be experiencing smaller spaces around you, in the same way as you experience the macroscopic dimensions. So therefore, in some sense, the first statement is that you don't really, you don't really know in which dimensions you live in. You can only say that you live in three, at least three macroscopic dimensions and one temporal dimension. But what the other dimension is, you could say, I don't know, and that's the way I think we would say it to begin with.
0:18:37.2 CV: Namely, we don't experience Them 'cause they might be very tiny. And so you could imagine at every point in space, another tiny circle or many, many circles of different dimensions or spheres of different dimensions at each point in space. And if they are so tiny, you wouldn't see these other dimensions. So your eyes not sensitive to them or more precisely. Our experimental cannot see that find a detail to distinguish it. And it's true that in string theory, at least the most, natural putative corner, the corner in which we have a classical string theory emerging, indeed has nine spatial dimensions and one temporal one. But it doesn't imply that these nine dimensions are all big. It could be three of them are big, six of them are small or whatever. So therefore there is no a priority contradiction with string theory itself being describing the universe we live in.
0:19:35.2 CV: And that's only one corner of this bigger theory. The string itself is only one corner. So we don't know whether we are at that corner or a different corner where there's no actual one dimensional object or process the two dimensional object instead of a one dimensional string excited. Maybe there's a two dimensional object excite relevant for the discussion. We don't know which exact corner we are at. So therefore the state now, which dimension we are at will also depend on that. Because, for example, another corner of string theory can have 11 dimensions, 10 spatial dimensions, that one temporal one for example. And that's called the M theory, Levi, which membrane becomes an interesting object and so forth. So depending on which corners we are ending up, we will have different descriptions. And perhaps I would say that.
0:20:22.1 CV: The lesson of dualities is that we cannot say exactly what is the dimension, the dimension of the physics, because we can only say in this particular corner, it looks like this many macroscopic dimension is the right picture. And then there are some internal dimension, which is hard to disentangle and see, because there could be dual descriptions of that one in particular. So the notion of dimension is also not an invariant concept. So just like the notion of what is basic fundamental entities is not the right concept, it's not invariant concept. You cannot make precise what you mean. What is basic fundamental entities. It's only gets a meaning in some particular corners. This the notion of dimension also does not have any di-notion and it gets its meaning only in specific corners of parameter space.
0:21:09.3 SC: Do we think this is getting a little, I worry this is getting a little vague. So we're, this is this famous you have in mind, and I have in mind this famous picture of M theory where it looks like a six pointed, kind of blob and M theory is the whole thing. And there's the different points are different varieties of string theory. Is that basically right?
0:21:32.1 CV: Well, I was not, some people doing say exactly as you just said. I was here alluding to M theory as one of the corners, not the whole thing. You can also, some people have called the whole thing, but I think that confuses the issue because the reason I don't like that terminology is that usually the 11th dimension is viewed as the M theory corner.
0:21:50.7 SC: Fair enough.
0:21:52.0 CV: And some people thought that is the whole description and that's not the correct way of saying it. So it's more democratic. One corner is 11 dimension, and that one I'm gonna call M theory. The rest of it, I'm not gonna call any particular theory. Some people do call, continue, call it the whole thing, M theory or string theory, if you wish, even though string theory has 10 dimensional limit 11. So that's up your taste in some sense. So sometimes I call it the whole thing again string theory because that's where I looked at it anyhow.
0:22:19.2 SC: Well, I was gonna say like, you don't even have a name for the whole theory that well keep.
0:22:23.2 CV: That's why people made up M theory as a word or string theory. I usually, I use the word string theory from that whole thing.
0:22:29.2 SC: And do we think, and this is obviously something we don't know, so it's okay to have a vague impression. Do you think that the real world lives or the world of our everyday experience, let's say lives close to one of those corners where things look more or less like a certain kind of string theory? Or is that something we just don't know?
0:22:46.5 CV: I think in some ways, I believe at our universe is near one of the corners. And this one I can get, get to a bit, in a bit more detail when I talk about some aspects of the string theory where I'm myself very excited about. So I do believe, and I will elaborate further later, perhaps, why we think we might be near one of these preferred corners. And this may not be the string corner, but some other corner.
0:23:09.9 SC: Okay. Very good. And, one question, this is just because I have you here, and I've wondered about this for a long time. If there are extra dimensions and they're curled up, they're compactified to something very small, presumably near the Planck scale, but the Planck scale is also where quantum gravity becomes important and our notions of space time begin to break down. Is it even okay to think of them as dimensions of space or are they fuzzier than that?
0:23:37.0 CV: No you said that very well, precisely because of what you said. That's why I was saying, in answering your previous question, the number of dimension is a bit ambiguous. Precisely. Because different pictures will give you different ones in that regime where the curled off dimensions are very small like Planck scale, therefore the notion itself is a bit ambiguous. That's why I wouldn't answer it that way. I could, we could more unambiguously answer what is large. And those are the ones which would make more sense. But what is the net dimension of the space time depends on the corners.
0:24:08.0 SC: Great. Okay, good. But nevertheless, this picture of curling up our extra dimensions is very, you know, visually tangible. We like it, and you're gonna explain this better than I can, but apparently there are many, many different ways to curl up those extra dimensions and that gives us many, many different options for what physics in our four dimensional space time ends up looking like.
0:24:30.9 CV: That's right. So if you start with nine spatial dimensions and one time, the most natural way to curl up is the six extra Spatial dimensions is simply by taking six circles, basically each dimension could be a circle and just take a, what we call the product of six circles or sometimes called six dimensional Taurus. So this is just basically taking, these, angular directions and six extra of those in addition to what we usually call X, y, and Z or this, the three spatial directions. Now that particular example I just told you is an example where Einstein's equation is solved automatically. So, or more, precisely in this case, string equations are also solved. In other words, this gives you a consistent background for string theory. Namely, if you started with taking six extra dimensions to be six curl up circles, then it is a nice stable static solution to our universe.
0:25:34.1 CV: It's not our universe, but it would be a universe. It would be somebody's universe perhaps, but not ours. The one I just told you would have too much, other stuff that's not seen in our universe. But it would be a viable, potential viable three-dimensional spatial theory with one temporal one which is static and nice and spatial, with which has symmetry, which certainly we don't see in our universe at Low energy called supersymmetry, where it tells you that there equal number of boulders and firmus with interest, with related interactions between them with special properties. This supers symmetry is, which automatically follows from the example I told you, but it's not enjoyed in low energy at our universe. So therefore it cannot be our universe.
0:26:22.1 SC: So one down. How many other ways are there to curl up those extra dimensions?
0:26:25.3 CV: There are many ways to do it. And, there are ones which satisfies Einstein's equation or the analog of the string equations. And there are a huge number of those. Many of them have fancy names like Calabi-Yau manifolds. These are, after the two math editions who propose and prove the existence of such spaces. And these give you nice properties that means in particular, it respects the super symmetry that the theory starts within 10 dimensions. And you can use these as your backgrounds for string theory. There are huge number of those, and there are millions or whatever number of them, and each one of them itself can have sizes and shapes to their, for each one of them, there are infinitely many choices depending on what radii you choose and what sizes you choose and so forth. So it's not, depending on what you mean by how you counted, you can say infinite or you can say finite different types of two choices of radium things.
0:27:28.2 CV: But there's a huge amount of them. So we have a huge set of examples when you respect some amount of this mysterious or not mysterious supersymmetry, which is not enjoyed in our universe. Now, when you come to our universe, which does not have supersymmetry, you're out of luck. It turns out that essentially all the solutions, well, not essentially, exactly all the solutions we know in string theory, which don't enjoy supersymmetry are not exactly stable. In fact, that's in some sense I would say a prediction of string theory. String theory tells you our universe cannot be stable. That means that whenever you break the symmetry, you are in a difficult, in a dangerous zone, namely, you do not expect, you should not expect a stable static universe in that situation, just like our universe and so on forth.
0:28:22.9 SC: Well, I was gonna say, how bad is that? Our universe is not static. It's expanding. Is there some cosmological way out of this issue?
0:28:32.1 CV: Well, one might have thought we were expanding because of some initial condition, and maybe after we end up a long time, you have basically, if the picture of dark energy or the cosmological constant were correct, one would've said, oh, after a long enough time, everything washes away and you have just a nice space, which is exponentially expanding, but basically otherwise it's static in some form. Now up to this exponential expansion. And you might think that's it, but it seems like that's not possible in string theory, I didn't neither something has to give way. And so therefore even that's not possible. So, whereas we could have contemplated of such a thing be possible from the viewpoint of just writing classical solution to Einstein's equations with a cosmological constant. That apparently cannot be possible in a context of string theory.
0:29:25.6 SC: Well, we're certainly gonna get into that, but how does this connect with the idea of the string theory landscape? Because my impression was that in the landscape of all possible compact afflictions, some of them would have a positive cosmological constant, just like we think our universe does. That was, that's how Lenny Susskind wants to solve the cosmological constant problem using the Anthropic principle.
0:29:47.6 CV: Yes. I'm not sure I sign on to that picture.
0:29:51.3 SC: Okay.
0:29:51.4 CV: First of all, I should say that there are still no reliable solution in string theory with a positive stable cosmological constant or even semi stable. Nobody claims a stable cosmological constant. They want to talk about cosmological constant, positive cosmological constant. They suggest that maybe they have a meta-stable. So even, there's certainly no claim in the literature of an absolute stable positive energy. Positive because there always, when your potential goes up, in strengthening invariably at far enough distance in field space, it goes down to zero. So therefore you never will have an exactly stable one. Now, the meta-stable ones, which would be these kind of potential places where you have a local minimum for the potential whose value gives you the cosmological constant, that's what we mean by cosmological concept. The value of this potential at the dock of minimum, even those have not been constructed with enough reliability. So in fact, we believe that this is not, this is very difficult to establish their existence or lack thereof for a very good reason. The reason is very simple. We can only reliably compute things in string theory when you don't have supersymmetry, only when you have, when you are near a classical corner.
0:31:12.5 CV: Near the classical corner, you can show rigorously in string theory that there is a potential, if there's a potential, like you break supersymmetry, which exponentially goes down, therefore there is no critical point. So in the classical regimes where the computation is under control, you know there cannot be even a meta-stable. Now you say, oh, okay, so maybe it's not the, classical corners are a bad place to look at. Maybe we should go a little towards the inside, but precisely when you go inside, you lose control of your calculation. And so people who are hoping or claiming to have solutions are on a dangerous path. They are trying to go to the regime where the classic, they know the classical description is beginning to be bad, but they're hoping they can argue enough. They have enough control to argue the existence of this one, which is not quite at that far corner.
0:32:00.6 SC: Right.
0:32:00.7 CV: And that is why this thing is even debated because we know that in the cases where it's not debated, it's impossible, to get there, the regions where it's undebatable, it's impossible to get there.
0:32:10.4 SC: So I think this is a super important and subtle issue that probably has not percolated very clearly out there into the world.
0:32:17.7 CV: Yes.
0:32:17.7 SC: So I want to just nail it exactly down. We can sort of, I'll rephrase it and you tell me you'll fix it. We can hand wave our way into imagining ways of compactifying the extra dimensions so that we get positive cosmological constant, negative cosmological constant, whatever. And that gave people this idea that maybe there was this landscape of all these possibilities. But what you're saying is that when we are a little more careful and try to really establish that these compactifications are safe and will last for long cosmological periods of time, we can't do it with the positive cosmological constant that maybe nature wants us to have.
0:32:58.7 CV: That's correct. We don't know. We don't know. So let me explain the difference between positive and negative values.
0:33:04.4 SC: Yeah.
0:33:04.8 CV: So as I mentioned, we have arguments why far enough in field space, the potential goes to zero. If that's the case, then negative one can be more stable because the negative one can be at the bottom and you go towards zero at the far end, and they could be absolutely stable. In fact, only the negative ones support exactly stable solutions like in supersymmetric cases.
0:33:27.2 CV: So negative energy is fine. Not all of them are stable, but we do have stable ones with negative values of energy. And those are among the best understood examples in string theory, what we call the anti-de Sitter space examples. And a lot of interesting examples in string theory having to do with holography come precisely from this class. On the other hand, you might think it's just a choice of a sign. Just make a negative energy positive energy. What's the big deal?
0:33:51.6 SC: Yeah.
0:33:51.6 CV: And in fact, that is what happens to a naive picture of physics. That is, oh, it's just a potential. You just draw the potential with just shift the constant up. What is the big deal? That intuition is incorrect. The intuition that a classical Lagrangian can be written with that form is as easy with positive or negative misleads the physicists to think that means it's as likely or as non-problematic to have either side. And this has been actually the major point of this program that I can delve into more deeply, which is called the Swampland Program. At some point I can do that. That's related to the fact that not everything that sounds natural from the viewpoint of the classical Lagrangian is actually consistent with quantum gravity.
0:34:39.4 SC: Good. Yes. So I do want to exactly get into the Swampland Program. That's why we're here. But maybe first let's set the table by talking about effective field theories. And the fact that when we do when modern quant field theorists and particle physicists think about the world, it's okay for them not to know what happens at infinitely high energies.
0:35:02.6 CV: Yes, that's certainly correct. We don't need to know what happens at infinitely high energies, but it should still be a consistent picture.
0:35:10.2 SC: Right.
0:35:10.2 CV: That is so in fact, in some sense, quantum gravity tell you there is no natural meaning to that infinitely high energies on some notions that we keep sacred, like the space on time, etcetera. Break down at these limits. So there's no natural description where you have a lot of energy, for example, pushed to that one point. Now you can spread it out like in the black hole to a larger region and you're fine. So you can have a large, massive black hole with a huge mass. But if you pushed it into one point, then you get the descriptions that we don't think that's possible. So in other words, when we have something which includes energies having to do the Planck energies at the Planck length scale, because if you focus it much more than that in the Planck length, we don't think our description of space and time really makes sense.
0:36:00.5 SC: But nevertheless, we think that we can predict outcomes of the Large Hadron Collider. So naively, we have these Feynman diagrams, like you started off saying.
0:36:09.8 CV: Yes.
0:36:09.8 SC: We do these calculations, we compute corrections, we get infinities, we re-normalize as a whole bunch of things we say. And we think that for various reasons, quantum gravity and other high energy things don't matter for predicting the decay of the Higgs boson.
0:36:27.5 CV: Yes. So that's the picture that the particle physicists have. So let me try to explain that picture as you're alluding to. So there's a cherished principle in particle physics, which is decoupling of small distance from large distance physics. That is, you start with something which is going on macroscopically, like there are atoms and so on are going on. And at larger and larger distance scale, it's irrelevant for the details of what you want to describe. For example, if I look at a piece of metal or something, yes, there is made of some atoms that you may want to study if you wanna talk about some individual atoms and so forth. But overall, as a solid object, you have a much simpler description macroscopically.
0:37:09.0 CV: You don't need that much detail. All of them more or less look the same with some minor tweaking here and there. So this idea that large distance, you only have a few possibilities of what kind of physics emerges, whereas you can start with many, many different things at short distances, which wash out when you step back and look at it from a big distance perspective. So therefore, you don't need to know about all those details. Is one of the cherished principles of quantum field theory and condensed matter physics, and that we have learned, one of these basic principles that Wilson in particular emphasized about the decoupling of the ideas from the short distance or what we call ultraviolet physics and long distance, which we call the infrared physics. So that's the cherished principle.
0:38:00.6 CV: Now, this principle comes with one more ingredient, which means the far line. You can kind of integrate out as we call in physics or kind of find the effect of these short distance things at large distances by using a few parameters in the large distance physics. Once you specify what the large distance physics roughly is, namely you say, I want the large distance physics to have certain symmetries and I want it to lead in certain dimensions. Once you specify these things, then you can write down essentially a unique theory up to a few parameters that you cannot quite figure out because all those parameters have those symmetries. So what you say, that's the viewpoint of quantum field theory, is that, okay, the short distance physics that we don't know is irrelevant in every detail except possibly figuring out these few constants, finite number of these parameters. So you see, You know what, I don't care about the short distance physics.
0:39:03.6 CV: I will just start with this larger distance perspective and choose the parameter that I like or I observe in my experiments and that's good enough. So therefore, by and large, it says that that complication of the short distance is not relevant to my perception or description of a larger distance physics scale. And that has been a cherished principle of quantum field theory, condensed matter physics. Everybody loves it. It's sometimes called the effective field theory description. It means effectively how you describe large distance physics does not need too much detail other than those few parameters that you can adjust at the end. That's the motto if you wish of this quantum field theory paradigm. This paradigm miserably fails when it comes to quantum gravity. That's the basic point.
0:39:50.5 SC: Right. So I will pause to give the listening audience an advertisement because I have a book that just came out that goes into effective field theory and sings its praises in great details and they can find all the details there. And now we're gonna for the rest of this podcast see how it miserably fails when gravity comes in there. And so and I guess that the source of the miserable failure is that when we have a low energy infrared as we say effective field theory we still like you alluded to have the we imagine that there is an ultraviolet completion that there is a way to make it completely consistent including all the energies that we might want to look at. But but maybe that's not right.
0:40:32.8 CV: Well we should have a theory which describes everything. And there should be ultimately answer to all questions that you may wanna ask. It shouldn't be like the theory only regardless of our ability to compute the theory has to have an answer for every question that's regardless. So it should be consistent self-consistent and so forth. So what we learned in quantum gravity via studying string theory was the following. We had all these kinds of ways where we could compactify the space and curling curling up these dimensions and come down and we see what we got in three plus one dimensions. So we curled up one wave we said, "Oh interesting. We get this gauge with these many particles." That's one other thing. This other thing, "Oh you got interesting, other thing." So we played around a lot with this kind of thing and then we noticed there were certain things we're not getting. In fact we noticed that what we are getting is very limited actually. And we were surprised. We were kind of saying, "Wow what is what is going on? Are we just not being imaginative or is there a good reason we are not getting other stuff?" So I will give you one very concrete example.
0:41:41.5 SC: Yeah.
0:41:44.0 CV: As I told you the theories which we really understand best are these theories which have the super symmetry the symmetry between both and style fermion. And those are the ones which we have the most controlled over in terms of computations. So you say from a perspective of a four dimensional observer like we are, suppose I'm interested in a theory which does have super symmetry.
0:42:09.5 SC: Fine.
0:42:09.5 CV: What are the possibilities? Well there depends on how much super symmetry you have and so forth. You say okay, I want to have a maximum amount of super symmetry consistent with having some matter. What would that give you? Well there is a particularly maximal class with super symmetry which includes forces like gauge particles and so on which is called n=4 in terms of the number of super symmetries four super symmetries in four dimensions. That's the maximum one you want. If you wanna have matter you say great this is what I'm interested in. Good. Now you say what do we know about quantum field theories? Forget about gravity with these symmetries.
0:42:49.1 CV: Indeed such theories are characterized just by choice of the gauge group. The group that controls the forces between these particles, like the same group that for this standard model is SG3 times SG2 times U1 whatever that group you choose for this theory completely specifies the theory right? So you say good it's very easy.
0:43:09.6 CV: Nice. So what do I do with this? Well you can just study quantum field theory. Forget about gravity. You study it without gravity and you find this is not only a well-defined theory, y but thanks to super symmetry is finite. Wow. This is a property that usually in physics we don't see.
0:43:25.2 CV: Usually when you have finite diagrams and quantum field theories you have all these complicated infinities that you have to make sense out of thanks to this normalization group technique which is what I alluded to to Wilson's idea about integrating out small distances away from the largest distance. But these theories with four super facilities do does not have this issue at all. It's finite for any group you choose any group with no matter how big a group you have in for example if you have SG2 and SG3, if you have SG3 SG4 any SD and you choose for the group it's a finite theory no matter what and you choose good. So that looks good. Now you say oh but this does not have gravity. I want gravity in the mix. So you say oh no problem just what we say in physics couple it to gravity. So we add gravity into the mix hoping for the best because you know this is a beautiful finite theory.
0:44:16.6 SC: Yeah.
0:44:18.2 CV: You add four dimensional gravity to the mix and you find you never get anything bigger than SU 23 SU 24 and higher don't exist don't come out ever ever. Now you say oh maybe that's because I'm being lazy or my string theory is unlimited and I better think harder and so on. We have now learned by studying more about why doesn't you get these ones that you cannot get these ones by some simple ideas related to the what general properties we expect quantum gravity to have. So therefore what you find is that even though you could have had any end naively from one to infinity consistent with SG one SG two SG3 et cetera up to SG infinity all of them are finite.
0:45:04.1 CV: When you could gravity you have a finite allowed set. So the set of possibilities compared to the totality allowed one is measure zero. In other words if you were if somebody threw you threw out you a group you could without thinking say it's not possible with gravity because you would be right. Because the the the ones which have gravity in them is measure zero the chances that somebody got it right it's so small. If they just choose a random one from one to infinity. So therefore this is the reality of string theory. We learn that the naive picture that we say oh nothing no problem. You can just put anything you want. Even in such a beautiful simple consistent finite theory without gravity totally gets messed up If n is beginning on 23.
0:45:51.3 SC: Good. So this is I take it that this is the origin of the swampland idea that there are a lot of effective field theories we could write down but not all of them. In fact most of them can't be derived from string theory or some other purported ultraviolet complete theory of gravity.
0:46:11.1 CV: Yes. We believe that there is there is most of these theories that people think, are possible from the naive field theory perspective, fails miserably when it comes to gravity. And it's actually easy to see why it could have happened that it's like this. So let me explain.
0:46:27.7 SC: Please.
0:46:30.2 CV: From a perspective of Effective filters. What the way to explain it to an effective filter is why they should have expected something crazy to happen. So this idea that low energy and short distance which is high energy or long distance, which is short, low energy, why these two things are decoupled cannot work with gravity. This decoupling between these two points of the idea that gives rise to the effective filter fails for an easy reason. The easy reason is this supreme object. The most mysterious objects in quantum gravity, which are black holes. The black holes run the show in quantum gravity, and they're the most enigmatic, but most beautiful objects in terms of what kind of things we have learned from them. So I will explain one aspect of them, which I want to, bring out now, which is the observation of beacon sign and Hawking that black holes carry entropy and the bigger black holes carry more entropy, the entropy being proportion, entropy meaning the number of degrees of freedom that this, particle or a state with this much mass could have which grows huge amount.
0:47:47.6 CV: So the entropy goes like proportional to the area of the black hole area of the horizon of the black hole, or more precisely one quarter of it in Planck units. So that's the formula for the entropy, which means that the number of particles, which have a mass or number of states, which have a mass equal to the mass of the black hole, is exponential of this huge area if you're talking about the macroscopic black hole, so this is... So what I'm describing to you is a prediction for high energy states in the quantum theory of gravity. If you take the mass to be huge, that the general of state is getting more and more thanks to this area of building larger and larger. But how do we know that? We know that using large distance physics, which is the low identity physics, namely we are describing it using eye size equation, which is valid for large distances, and that's how beacon and hawking doing only a tiny correction to classical gravity.
0:48:49.0 CV: We're able to deduce this by just a tiny quantum correction, or what we call semi classical gravity competition, establish these facts. So what we are learning, just from the thinking about black holes, that large distance or low energy and high energy are linked intuitively, and we cannot disentangle them. So this idea that one feeds into the other is crucial in this whole idea, and this has been why this picture of effective filter theory fails that in general notion, of course, it doesn't mean that you cannot describe physics at any given scale using that scale. That's of course always true, but it doesn't mean that you can get anything you want because the consistency of how that fixes in with the lower energy is very intricate. And that intricacy is what forces the whole thing to be a very finite and limited set ultimately.
0:49:40.6 CV: That's the basic idea for this, for this idea. So let me then again, let then try to package it in a different way. If you start with a given quantum field theory, which looks perfectly consistent, like the example I told you about the super symmetric one with arbitrary group, that would've been a potential consistent theory of quantum gravity. If you mix the gravity with it, I told you they are not so I would say that a putative theory, which could have been okay with gravity, but it's not, we say this belongs to the swampland.
0:50:18.5 SC: Right.
0:50:19.3 CV: The ones for which actually can be completed to a complete theory of gravity, we call landscape. So swampland and landscape in that sense, they're not too different from each other. You could have thought it's part of the landscape, but upon further scrutiny you might find actually it doesn't work. So that's what we call it swampland. So we believe, as I was explaining that essentially every theory is in the swampland. Any, theory you can conceive of is the swampland. Not only very rare ones, the jewels or the actual ones for which quantum gravity can work on. So the quantum gravity are very specialized, very specialized. Now this leads to, saying, okay, how do you know how do you pick these jewels? How do you find which one of them are good? Now which ones are bad? Of course, it's very hard if you have a measure zero set to say, what is that measure zero have, it's much easier to say what is bad.
0:51:15.1 CV: Maybe you say, oh, if it's on this side of the parameter space cannot be happening, or if it's this side, it cannot happen. So that, that's why the program is that I've been working with a number of colleagues. It's called the Swampland Program to identify the bad ones. Not that we are interested in the bad ones, but that's the easier thing to do. Yeah, you can rule out what doesn't work. This area is bad, that's bad. To narrow down where the jewels can lie. Fixing the jewels off of course, very difficult. Because you have to really fine tune all the parameters get actually a theory.
0:51:46.5 SC: So if we want the audience to take away a motto here, gravity is truly different than the other forces. It's really causing us to think differently about all these important questions.
0:51:57.2 CV: Exactly. So gravity and led by this beautiful object, black hole.
0:52:01.6 SC: Yeah.
0:52:03.4 CV: Is the real reason when you bring in the quantum aspects into the mix, which is behave so differently, so differently from quantum field theory. So gravity is a new, kind of a theory, which you cannot just think, oh, it's just like the old stuff. You just add in one more field. Not so. Not so.
0:52:22.8 SC: Yeah. [laughter] Okay. Can, is there any simple, nice, tangible example of something we've learned from the swampland program about what kinds of theories cannot be consistently part of a quantum gravity theory?
0:52:36.0 CV: Yes. One of the ones that is one of my favorites is what's called the weak gravity conjecture. Now, many of these things that we, call these swampland properties, we call conjectures because we don't know how to prove them.
0:52:48.7 SC: Yeah.
0:52:49.3 CV: Because we do not have the underlying theory. So, we bring it as principles or conjectures. So one of them is called the weak gravity conjecture. Now, what does this imply? What does it say? It says that if you, so suppose you have a theory consistent and coupled to gravity. So gravity exists in it. So you have some electric forces in that theory. So electromagnetic forces.
0:53:15.8 CV: It's saying that in that theory, there should be some elementary particles which are charged under that electric force for which their electric repulsion, if you bring two of them next, the same one next to another one, electric repulsion is much stronger than their gravitational attraction. In other words, the gravity is the weaker force. In fact, it's always the weakest force. So it said differently the gravity, if you have two particles of same mass then the gravitational force goes like a square of the mass product of the masses will be square of a mass. And if you have electric forces, they go like electric charge square. That will be the repulsion force of let's say two electrons. If you bring them next to each other, it's saying that the electric charge is much bigger than the mass measured in Planck units. So the mass of the electron measured in Planck units we're saying is much smaller than the electric charge, which is very much true in our universe. The electric charge is a much more stronger force in our universe than the weak meager electric force within two electrons. So now you might have thought, oh, it's just a parameter.
0:54:15.8 CV: I can't just take the mass of the electron, make bigger and bigger and bigger. So it's bigger than the electric charge one, when you measure some plaque units, in which case the gravitational force would be stronger than electrical repulsion, what's the problem?
0:54:49.0 SC: Yeah.
0:54:49.0 CV: There is apparently no problem from the viewpoint of the effective field theory naively you can write down. And so the with Wilsonian viewpoint would've been no problem. Just write it down. However, we know this is not possible, and there's even a heuristic argument for why this should not be possible using black holes Physics. This is not a rigorous argument, but I will basically try to sketch what the basic ideas. If you look at the massive black holes with a given charge, there is a restriction that in fact it goes the opposite direction. That if you have a very big massive black hole, this mass is always bigger than or equal to its charge, unlike the elementary part that I'm talking about, for which I'm saying that mass is less equal to charge. The gravitational one tells you when you solve the Einstein equation, if you want, don't wanna have a bad singularity. It's always the other way. Okay, so what am I saying there? Well, if you take into account that you start with one which is barely the masses equal to charge, which is the boundary of possibilities for the big black hole.
0:56:15.8 CV: And if you assume it decays, allow Bekenstein and hawking or Hawkins decay, in fact if you assume it decays, which we cannot prove but we believe it to be true for all the examples which don't have super symmetry. So if you have like a black hole in our universe, we think it's gonna decay even if you start with mass equal the charge. Well, if you emit a mass and a charge like an electron, if the mass and charge were opposite way, if it was the same way than the back, if the mass of the electron was bigger than the charge, then the resulting black hole, would give you a mass, which is less than its charge, and that's inconsistent. So therefore there should be objects which you can emit, which have the opposite relation and which the gravity is weaker force. So this is a heuristic explanation of why this kind of thing can be related to black hole physics and could be consistent. What other evidence do we have for this? Well, in all the examples of string theory, it's true in many cases in a very non-trivial way.
0:57:05.8 CV: So therefore we have a lot of examples from string theory supporting this. But as you saw, the argument that I gave you are at least heuristic as it may be, did not use anything to do with string theory. It was about black holes. So this happens to many of these principles. We kind of see the string theory, I would see, oh, that's curious, can we have a better explanation? And then we try to appeal to more fundamental physics like properties of black hole and the consistency of their evaporation and this and that to try to see if we can have at least the heuristic explanation. And that is the nature of these kind of arguments.
0:57:30.4 SC: And just so we understand what the expectations are once we get very good at this and figure out everything that we can, you're not actually hoping to end up saying it had to be the standard model of particle physics. We're not gonna be that specific in narrowing down the swampland.
0:57:45.2 CV: Absolutely not. Because as I explained for example, we know that all these super symmetric examples are perfectly stable, consistent, and not our universe. So we are not under any illusion that we are gonna derive our universe in this way. Of course we are assuming that our universe is the consistent one. Otherwise, what are we talking about? But that's not our hope. So let me explain what is our hope and then I will explain what we have been doing with this hope.
0:58:13.5 SC: Good.
0:58:15.9 CV: Our hope is to use observation as an anchor combined with the principles of the swamp plan to make the next prediction. In other words, we wanna say that some observed facts in our universe that are not accidental. We may not be explaining all the facts, but if you have fact A, maybe fact B follows, now you might ask, why is the fact a true? I could say, I don't know. It happens to be we live in this universe, but then it a to then B better be true. Now you say, okay, why can't we do this without using any of this swamp plan? The problem is that in the case of if you view the effective filter perspective, it does not allow you to de do such a statement. If A is true, it doesn't allow that necessarily B doesn't follow, B only follows because of this very limited possibility of what is a consistent theory of quantum gravity. So you say, oh, if you ever found the quantum gravity, which we know is very hard to get, of course, which has a property a better have property B, even though from effective theory, there's no actual explanation from A to B, but from string theory principles, there is.
0:58:55.9 CV: So therefore we wouldn't say that, oh, we have derived the whole universe, et cetera, et cetera, but we correlate facts in our universe using these ideas, and that's what we have been doing. So I will explain one fact, which I think is one thing I'm most excited about, which is comes back to your question that you raised, whether or not we are near one of these classical limits in the context of street theory. So I would explain why we think we might be near one of these.
0:59:54.0 CV: So one of the things we learn from string theory is this bizarre fact, that whenever you choose your parameters in your theory to extreme values, you not only can get some kind of a classical picture, you always will get some classical picture. In other words, there is no extreme regime of any parameter in our physical theory for which it's not a classical picture. So therefore we say, oh, this is an interesting fact. So going to extreme regimes of parameters, take the parameter towards zero or towards infinity, it better be that some new classical picture emerges. This always happens.
1:00:34.1 CV: And this is the duality I was alluding to. Do we have a proof of it? No, we don't have a proof of it. Is it true in all the examples of string theory? Yes. So we take this as a principle that extreme parameters in physics means there's a dual description. Without knowing what that description may be. Now, we have also identified what could be, in general, what are the allowed possible ways you can get the dual description. And we have only found two types of ways we can get these dual descriptions.
1:01:09.5 CV: What happens as you go to these extreme parameter regimes is that either some dimensions get bigger and bigger that you were originally thinking they were curled up and tiny, they could get bigger and bigger, some number of them, one, two, three, whatever number, or what could happen in other extreme parameters is that these dimensions don't change size, but some string becomes lighter and lighter and lighter, and you get a tiny, tiny tension for them. You get a tower of very, very light strings.
1:01:34.9 CV: And these are the only two possibilities we have ever seen in all the cases in string theory. So either some number of dimensions open up, or some strings become light and tensionless, what we call. Ours have almost no mass, just like fundamental strings are, light strings. So now we come to our universe. This is the general principle, what's sometimes called the distance conjecture, which means if you go a large distance in parameter space, you get some dual description. And sometimes it's called the duality conjecture. Basically, it means at large distance, you get the dual description.
1:02:11.1 CV: So we come to our universe and say, okay, let's apply this to our universe. There's no parameter. There are these parameters like electric coupling and so on, but they are not particularly big or small. E squared over h bar C is one over one at 37. It's not big or small. It's kind of like there, what we call order one perhaps. But then you think harder, you say, oh, come on, there's an obvious one. It's a big elephant in the room, which is the dark energy.
1:02:37.4 CV: To the minus 122 in fundamental units of physics, by all measures, breaks all the records for smallness or extreme values other than zero. So we say, okay, there is. So that means the very fact that we have Cosmological constant so small means we must be near one of these corners. Now, you could say, oh, okay, so let me just apply this principle I have seen in string theory to this case in our universe. Lambda, the dark energy is small. What could it be? Well, it could be either. So first of all, then you can ask, okay, when you get this light, so at these extreme powers, extreme parameters, what happens is that you get the tower of light particles.
1:03:22.9 CV: And this tower of light particles scale with some power of this parameter. So in other words, we expect more than just as the cosmological constant, which let me call it lambda. As lambda goes to become very small, like 10 to the minus 122, there are some particles whose mass scales like that lambda 10 to the minus 122 to some power.
1:03:42.1 SC: Yeah.
1:03:42.6 CV: Where that power is of order one. We don't know what that order one parameter is, but something of order one. This is the general principle we are being told. Now, you can give arguments of what is the range of that parameter, and you can give an argument that this range should be in our universe between a half and a quarter.
1:04:00.3 CV: In other words, the mass should be the range between lambda to the half to lambda to the quarter range. And then you say, okay, armed with this, first of all, what is this parameter? What, sorry, what is this coefficient? This is what values is between half and a quarter? And what is this light tower of particles? I have not seen one. The standard model is not that, and so what is it? We are saying that there's a light tower of particles, but without getting into any detail, we just say somebody was telling us about dark matter.
1:04:33.4 CV: And more than that, the tower and string theory is predicted to be weakly coupled. So this automatically, without doing any thinking, says, oh, could it be that the smallness of dark energy and existence of weak interacting dark matter are related? This says yes. So this automatically, without doing any kind of thing, suggests connection between dark energy and dark matter. That is, in some sense, they come off bundled, unified. The existence of smallness of lambda would say that there is a tower of like paradox. Now would whose mass would go lambda to the quarter. Anyway you check then you go an expense can I check whether this is true or not. You prove that the only value of this exponent that could possibly be true or not in universe because all the rest are ruled out, is one quarter, all the other ones you are sure they are already violated by experiments we have already done.
1:05:25.7 SC: They are experimentally ruled out not theoretically.
1:05:28.0 CV: Experimentally ruled out. Exactly. So this is the principle I was telling you. We do not know how to figure out what a universe is but something we can express the observance, some principle can result into something else, we see, therefore we are saying that there is a power to one quarter. And now we can say, oh okay, so what is this power, Is it the, is it some dimensions opening up or is it some parts of dimensions getting big or that's does harm any of them or is it string going on, again you use observation to rule out all the possibilities except the possibility of one extra dimension opening up with the size of the older of one quarter which is about microscopic. So, Again, just by observation, combine with this principle, youre fixed with a unique possibility of having one microscopic dimension, so out of these dimensions, one of them is not as small as the rest. It should be of the older of about 1-10 Micron or something.
1:06:26.7 CV: Add More than that, the dark matter would be these oscillations of gravity in these extra dimension. In other words, it unifies dark matter with dark energy and with gravity, maybe gravity. Dark matter is graviton. The zero mode of the excitation is what we call our mathless graviton. These other excitations is dark matter. Why is it weekly coupled? Because gravity is weekly coupled. So we don't have any... In other words, we're not putting any, like, throw in another particle, that we call it dark matter or do this and that. And by the way, it's really to dark energy. So all of these things come actually quite elegantly connected and actually gets connected to the neutrino physics, which is also has the same scale as down with to one quarter. And you can actually see that the fundamental Planck scale in fifth dimension is not the usual class here, but much reduced by factor of 10 to the nine or so to about 10 to 10 G.
1:07:27.4 CV: So in other words, you get a totally different physics and you find that all of these scales, like the 10 dimensional physics scale, is cosmological concept to the 1/12 power. The weak scale is cosmological to the 2/12 power. The neutrino scale or the, this tower of dark energy scale is down to the three twelves. The Hubble scale is down to the six 12th and so on. So you get very natural simple powers that you can actually compute like one 12 that, so you can actually compute one 12 comes from four times three where four initial space sign at threes coming from five initial Planck scale having an implant cube in the formula. So you put all of these together and you get this natural hierarchy of scales coming out from one parameter, which is this lambda being so small. We cannot explain why lambda's small. We cannot explain why dark matter is small.
1:08:18.4 CV: But if you take that small, then you get these other scales which are automatically hierarchic in the way of the kind of scales that we actually do see in our universe. And more than that, it predicts the right amount of dark matter in our universe. So the amount of dark matter comes out right without fine tuning. So this principle of which is philanthropic principle is not needed to explain why do we have dark energy taking over just when dark matter and radiation temperature are equal? So that's one of the things that we bear basically suggested that, well we don't wanna have too much fine tuning for lambda for the dark energy, but only predicating on our existence.
1:09:04.8 CV: And our existence means the dark energy should not have taken over before the matter dominated at some point. So the existence of the galaxies and all that without the impossible, let's say dark energy was too much. And he put it just roughly the highest allowed possible one compatible with the matter, radiation equality, which gives like a coincidence back. That's why the dark matter to take over right after the matter. Radiation in cosmological defect almost at the same time, but very shortly thereafter. So this actually gets explained. We don't put it by hand. So you know, it works for any lambda. So for any lambda you get the same feature, so therefore there's no fine tuning there. So we don't need lambdas for that.
1:09:45.4 CV: Of course, I cannot explain why Lambda's small. So maybe for atrophic, maybe you need it for that. But this is the point here that some fine tunings can be ameliorated in this kind of a program because the fact that there are very few possibilities allowed already puts a huge constraint. And if you get one of these facts, then many, many things fall in place force. They're forced to be falling in place, which is very strange from the viewpoint of effective new theory, which is why from the modern particle physics perspective, they're having such a hard time explaining all these funny fine tunings that don't look natural. So those fine tunings for particle physics is kind of a lot of it. At least not all of it gets ameliorated by saying, oh, there should be a lot of something which appears as fine tuning. 'cause otherwise the gravity doesn't work. And the consistency of gravity drives the show.
1:10:38.2 SC: This sounds all very new and exciting and you're motivating me to, right after this podcast is over, I'm gonna download some papers and read about this 'cause I'm not...
1:10:47.0 CV: Yes. [laughter] there's if you do that, there is a particular paper I wrote for a review for people who are not string theorists. Called from bland dish predictions for our universe. So in that one, I basically described the basic motivations of what this program is and how does it give you what I just were was telling you?
1:11:04.7 SC: Can I ask just very quickly, I mean you have dark matter that is similar in mass to neutrinos you said, right?
1:11:11.8 CV: Yes, yes.
1:11:12.9 SC: And you get the right relic abundance. But is it cold dark matter?
1:11:17.5 CV: It is cold in the sense that it was never in thermal equilibria with us.
1:11:22.8 SC: Okay.
1:11:23.3 CV: But it is called, so it looks very much like, like Lambda, CDM except the door matter. These are made of these excited graviton states. They're not stable. So they're leaking down. Because they're the tower. But it turns out that decay down is so small because of the gravitational strength.
1:11:41.2 SC: Okay.
1:11:41.2 CV: Because they're suffer have the order one over and Planck in them. And the mass of these guys is very small. So the rate of decay goes like Cuba up their mass divided by square of the Planck states, and that's very small, so they're gradually coming down in mass. And so the dark tower is kind of dynamically rearranging itself.
1:12:02.1 SC: Right. Okay, good. I mean, I'm sure that that's like a whole nother podcast worth of questions here. But let's, maybe we can sort of bring it back to where we started close the Tarun, as it were. I almost said close the circle, but with the cosmological constant, which you've been referring to. So my impression was that as you said, we have no examples. In fact, we have reasons why it's hard to find examples of meta stable solutions in string theory with the positive cosmological constant. So how much are you willing to stick your neck out and say that the dark energy that our telescopes tell us is there. String theory says is not a cosmological constant but is something slow and dynamical.
1:12:46.5 CV: Okay to say it's dynamical? I think it's I can absolutely say namely all the things that we learned from string theory and quantum practice, there's no constant in any parameter in your Lambda branch and including the cosmological constant, that means that should be viewed as dynamic. Now the next question, is it whether it's stable or not?
1:13:07.7 SC: Yeah, that's what I... In other words.
1:13:13.2 CV: So the question of stability is the next question. So. We have given a proposal of what could replay, what is the principle which tells you how stable it is or it's not. As I told you, when you go to extreme parameter ranges, it cannot be stable because it rolls down. Now you could say, well, could we be near this region? But not exactly near the extreme region. And I was telling you, arguing for you that our radius of the universe is, we are near one of these extremes. How close are we to this extreme limit? Could we basically be near one of them with some other coefficient or somewhere near the top of a potential, maybe or a little... Okay. So what we did with the pseudo on mind a few years ago was to propose what we call the trans plan and censorship conjecture, which basically suggested that things which are smaller than the Planck length can never become physical.
1:14:01.3 CV: That it's a phantom. The things which are too small, it's just the space should not make sense. Neither should the fluctuations in that distance scale using that and the fact that these modes cannot exit the horizon and classically. We basically came up with some boundary conditions of what is possible for the dark energy. We found using this principle that the potentials that we get in strength theory should fall off at near large distance exponentially as we were seeing it with the correct exponent that we were seeing in string theory. Now, this principle also nevertheless, allows you to have a metal stable one. However the lifetime of it cannot be too much. Namely the lifetime of it is hobbled up to a logarithmic correction. So in other words, there's a bound on if it is on one of these metal stable one, it cannot be more than a few trillion years in our universe.
1:14:58.5 CV: So that means that we have an upper bound prediction of the age of the potential lifetime of our universe could be no more than the couple trillion years. However, the more natural possibility, of course it's evolving now. And I'm quite excited to see whether the recent observations by DESI, was just announced that had the preliminary results announced a few weeks ago where the dark energy may be evolving, may actually true, and this is too early to actually to be sure about, but it's an exciting possibility.
1:15:32.3 CV: I say that what I'm more sure about is that dark energy is going to go away long term, long term meaning certainly 2 trillion year time. But whether it's actually in our universe or not, I cannot be sure, but I would say that's the most natural possibility because as I said, we know it's going to go away at the Hubble time, up to lot correction, maybe it's just a Hubble time.
1:15:54.2 CV: And in fact, that's the scale in which the rolling is happening. So for us, the rolling unfolding in Hubble time is natural. So we have an explanation on that. That is, when you say to scope up these potentials, they're exactly of the type which unfolding takes place in Hubble time. So it's similar to the kind of things that they could be seeing in DESI. So I wouldn't be so sure until the experiments come out more decisively on one way or the other, but I certainly would think that's a very natural possibility for us. And so that makes it even more exciting. So for the next few years, what we have and one other experiment that we are actually currently involved with a group in Vienna, who's actually trying to measure the deviations for one of our squared force law at the Micron scale. We are predicting that the one of RS squared, because we have one more dimension, becomes one of our acute.
1:16:42.1 SC: Yep.
1:16:42.4 CV: If you go for Rs, which is less than a Micron or so, up to now, it has been measured up to distance of 30 microns, that it does not become one of RQ. So we are just at the border of this regime that we think something could be changing. And they're trying to actually do experiments. Hopefully within the next few years they'll get some permit results up to 10 micron. And so they're getting close to the regime of interest. That is interesting. So this one, the dark energy decay and axion physics, which I didn't tell you about also in this model, turns out to have the same mass scale as neutrinos.
1:17:14.5 CV: Again, something that could potentially be observed in near experiments in I saw that international axion observatory that they're making. So these could be observed also there. So there are many potential, venues experimentally that could shed light on our program as well as verify or check some of the predictions that we're making.
1:17:38.5 SC: So years ago I wrote a paper pointing out that if you just had a generic dark energy scaler field with super low masses, it would run into trouble with fifth forces and time dependent constants and things like that. Is there some fun string theory property that gets us out of those limits?
1:17:56.6 CV: So first of all, so certainly that's important. For example, the rate at which the Newton's constantly changing is less than 10 minus four. And if you go from the beginning of our universal apathy, like there's a bound percentage wise, so indeed that those are important balances that one has to make sure. And so whatever we are getting should be compatible with that. People have had some, I mean, some of my colleagues are contemplating, in fact they have been writing papers, not my colleagues, but long ago chameleon models and so on. So people have proposed some alternatives. So I don't want to say exactly what could potentially be, but of course the fifth, fourth ones are certainly a worry. If you ever talk about the evolution and that you have to be careful about. Yes, I agree.
1:18:36.3 SC: Okay, good. So, that was very exciting. I'll give you the opportunity to wind up with a more grand philosophical point of view question here. I mean, we ended up we started with the finiteness of Strength theory and Quantum gravity. Like you said, String theorists in the early days weren't even trying to describe quantum gravity. And String theory has spent decades struggling or just ignoring the question of connecting to experiments. But maybe now we're coming closer to being able to do that, or maybe not. It's all very, shiny and new and things can break. But is there some lesson to be learned here about just sticktoitiveness persistence, being stubborn in pursuing an idea that seems really good even though you don't quite know how to connect it to what you want?
1:19:28.9 CV: I think understanding what we have learned from Strength theory is crucial. And very often it's easy just to give up and just say, oh, there's so many possibilities. Our universe is too complicated. Come on, and so on. But actually, if we look at the lessons that Strength theory has taught us, and more broadly history of physics has taught us is that, ideas that are natural in some contexts could lead the way into things which look crazy at some point. I mean, extra dimensions that's already crazy sounding or things like I would say like black holes which now have been verified were crazy even to Einstein. So I'm just saying that things which sound crazy does not mean they are wrong. And in fact, if the theory naturally suggests these are natural thoughts, we should take them very seriously.
1:20:23.3 CV: Don't be afraid, go with them, make predictions, and don't be afraid of making wrong predictions. And I think that's something that some of my colleagues are a little bit perhaps worried about making predictions that can be disprove at, for example. Now that's understandable. On the other hand, in the context of song plan program, you make these assumptions which sound natural and based on these you get some consequences. And if for whatever reason those consequences are not verified express, you learn something about what were you missing in those principles? Try to get it improved. That's what science is. So I feel that we have lost track of what a scientist is sometimes we think we are gods, we should be able to tell you with a 100% certainty this is gonna happen.
1:21:16.9 CV: And if it doesn't happen, the universe is wrong. No. We should be modest. We're just trying to understand. We make these models and if it doesn't work, we go and refin on models. That's the way science is supposed to be. I think a little bit of this grandiose picture that, I know everything and so forth and so forth. Or I better say something, which is absolutely correct, is actually getting into the way of understanding nature. And I think we should go back to the more modesty, like putting what we have learned, taking the next educated guess based on those, and see what it predicts. And if it doesn't work, go and refine it and come back with the next one. That's what science is, and that's what I hope me and my colleagues should be doing.
1:21:56.8 SC: I think that's a perfect place to end Cumrun Vafa. Thanks so much for being on the mindscape podcast.
1:22:01.0 CV: Thanks, Chad, it was a pleasure. Thank you.

I would put forward the conjecture that this episode has the largest guest-to-host ratio for speaking time. (This is an empirical question that can be answered by analyzing the transcripts of all the episodes, if anyone wants to write a script to do that.)
What was the review paper Dr. Vafa mentioned? Anybody has a link for it?
I believe the review paper is https://arxiv.org/abs/2402.00981
Can anyone give me some feedback on this idea: The act of measuring 2 entangled particles at the same time rules out ANY hidden variable theory (local or non-local).
For example, if there is some hidden variable X shared by both particles, once particle A is measured, it hasn’t heard from particle B yet, so it chooses some spin based on X and the fact that B hasn’t been measured. Similarly for B.
So measuring the particles at the same time is equivalent to a local hidden variable theory which by Bell cannot exist (assuming measurement independence).
I found the short video posted below: ‘String Theory Explained- What is the True Nature of Reality?’ (1 May 2018) helpful in trying to grasp at some intuitive level what string theory is all about and how it might offer a guide to understanding the true nature of reality, or at least as close as humanly possible to understanding the true nature of reality.
https://www.youtube.com/watch?v=Da-2h2B4faU
Jake, if I understand your argument correctly, you’re suggesting that measuring the 2 entangled particles at the same time is equivalent to a local hidden variable, which by Bell cannot exist. But unless the 2 particles were at the same location how could you ensure they were being measured at the same time? Whether 2 events at separate locations are simultaneous depends on the motion of the observe relative to the location of the events.
Jake, you can’t take the argument too far, because standard quantum mechanics works, and you can think of it as a non-local hidden-variable theory, where the wavefunction psi is the non-local variable X. Of course, this type of theory can’t be ruled out.
In your case, a joint measurement, both X and the two measurement settings joinly determine the probability distribution of both outcomes. Bohmian mechanics also works in this manner. The variables in the model “communicate” at a distance, but this remains hidden in the sense that the outcomes never carry any nonlocal signals.
(Howard, it is actually standard to consider simultaneous distant measurements; of course that requires choosing a preferred reference frame, but that’s legitimate and is not a problem.)
By the way, note that Bell’s theorem also assumes causality. Bell did state that “locality” is an abbreviation of “local causality,” but never studied the possibility of models violating causality internally (with the outcomes never carrying any retrocausal signals, of course). Such models have distinct advantages; see, e.g., the book Time’s Arrow and Archimedes’ Point / Huw Price.
Nathan, do you agree with this flowery description of the so-called “Block Universe”, where the past remains fixed, like a fossilized record etched into the block, it’s as real as the present, but the future, like an uncarved section of the block, awaits its turn to emerge. – A realm where past, present, and the future coexist in a harmonious dance across the cosmic stage.
Ref: Microsoft CoPilot
Howard, your question is sort-of philosophical, and I don’t know the answer. I do use a variant of the block universe approach in looking at models where you can’t evaluate the internal variables (aka hidden variables) for time t_1 until you specify all the necessary inputs, including inputs at time t_2 later than t_1. But to make things easier, I assume that all of this occurs in the past. And I think the model is only an approximation of what actually happens in nature. We’re nowhere near achieving a full understanding of what is “actually going on” in quantum physics.