This year we give thanks for an idea that establishes a direct connection between the concepts of “energy” and “information”: Landauer’s Principle. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, and gauge symmetry.)
Landauer’s Principle states that irreversible loss of information — whether it’s erasing a notebook or swiping a computer disk — is necessarily accompanied by an increase in entropy. Charles Bennett puts it in relatively precise terms:
Any logically irreversible manipulation of information, such as the erasure of a bit or the merging of two computation paths, must be accompanied by a corresponding entropy increase in non-information bearing degrees of freedom of the information processing apparatus or its environment.
The principle captures the broad idea that “information is physical.” More specifically, it establishes a relationship between logically irreversible processes and the generation of heat. If you want to erase a single bit of information in a system at temperature T, says Landauer, you will generate an amount of heat equal to at least
![]()
where k is Boltzmann’s constant.
This all might come across as a blur of buzzwords, so take a moment to appreciate what is going on. “Information” seems like a fairly abstract concept, even in a field like physics where you can’t swing a cat without hitting an abstract concept or two. We record data, take pictures, write things down, all the time — and we forget, or erase, or lose our notebooks all the time, too. Landauer’s Principle says there is a direct connection between these processes and the thermodynamic arrow of time, the increase in entropy throughout the universe. The information we possess is a precious, physical thing, and we are gradually losing it to the heat death of the cosmos under the irresistible pull of the Second Law.
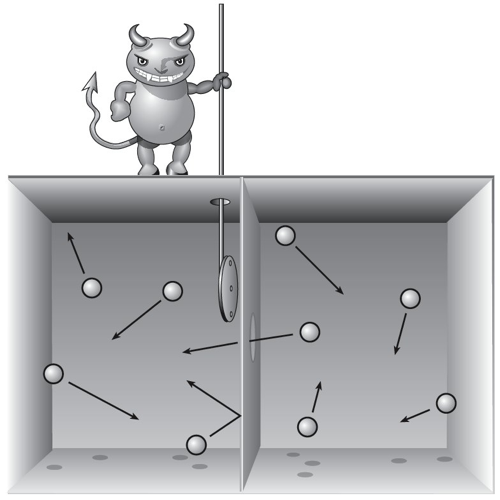
The principle originated in attempts to understand Maxwell’s Demon. You’ll remember the plucky sprite who decreases the entropy of gas in a box by letting all the high-velocity molecules accumulate on one side and all the low-velocity ones on the other. Since Maxwell proposed the Demon, all right-thinking folks agreed that the entropy of the whole universe must somehow be increasing along the way, but it turned out to be really hard to pinpoint just where it was happening.
The answer is not, as many people supposed, in the act of the Demon observing the motion of the molecules; it’s possible to make such observations in a perfectly reversible (entropy-neutral) fashion. But the Demon has to somehow keep track of what its measurements have revealed. And unless it has an infinitely big notebook, it’s going to eventually have to erase some of its records about the outcomes of those measurements — and that’s the truly irreversible process. This was the insight of Rolf Landauer in the 1960’s, which led to his principle.
A 1982 paper by Bennett provides a nice illustration of the principle in action, based on Szilard’s Engine. Short version of the argument: imagine you have a piston with a single molecule in it, rattling back and forth. If you don’t know where it is, you can’t extract any energy from it. But if you measure the position of the molecule, you could quickly stick in a piston on the side where the molecule is not, then let the molecule bump into your piston and extract energy. The amount you get out is (ln 2)kT. You have “extracted work” from a system that was supposed to be at maximum entropy, in apparent violation of the Second Law. But it was important that you started in a “ready state,” not knowing where the molecule was — in a world governed by reversible laws, that’s a crucial step if you want your measurement to correspond reliably to the correct result. So to do this kind of thing repeatedly, you will have to return to that ready state — which means erasing information. That decreases your phase space, and therefore increases entropy, and generates heat. At the end of the day, that information erasure generates just as much entropy as went down when you extracted work; the Second Law is perfectly safe.
The status of Landauer’s Principle is still a bit controversial in some circles — here’s a paper by John Norton setting out the skeptical case. But modern computers are running up against the physical limits on irreversible computation established by the Principle, and experiments seem to be verifying it. Even something as abstract as “information” is ultimately part of the world of physics.
Great post, Sean. Happy Thanksgiving!
Great post! I think there an error in the last sentence of paragraph 6? It should say that “…all right thinking folks agreed that the _entropy_ of the whole universe…”, right?
Happy thanksgiving!
Pingback: Thanks for Landauer’s Principle: entropy of erasing information. | Gordon's shares
Nice Post.
Regarding the controversial status there is a nice recent paper (http://arxiv.org/abs/1306.4352) formulating Landauer’s principle in a minimal setting and providing a rigorous proof.
Cheers
Oscar
I’m thankful for this blog.
Matt Lewis — totally correct, I’ll fix it.
I was focused so much on ISON this year I forgot about your yearly tradition. Something to cheer me up today.
Dr. Carroll,
I have two questions in reference to your post on Landauer’s Principle:
(A). 1. If all information is PHYSICAL, and
2. The laws of physics are INFORMATION, then
3. The laws of physics are PHYSICAL.
Therefore, how can you get a PHYSICAL universe from “absolute nothing,” which by definition is META or NON-PHYSICAL? re: Dr. Lawrence Krauss, and Dr. Alexander Vilenkin?
(B). How can information be irreversibly LOGICALLY LOST?; does this not contradict the CONSERVATION LAW OF INFORMATION? Re: Black Hole information loss controversy, Dr. Stephen Hawking vs. Dr. Leonard Susskind.
If “information” is ultimately part of the world of physics and all things physical are information-theoretic in origin (John Wheeler), then it seems the physical world and the informational world are one and the same.
T.E. Oakley, I was about to say the same thing I always say when people ask your first question. Then I realized that 1.) nobody wants to hear it again, and 2.) I should just write a book about it after I graduate so that I can stop living on discarded pizza crusts.
I’m an IT guy with an interest in fundamental physics, and whilst I have no issue with energy being a physical thing, I just don’t feel the same way about information. I could use coins as binary bits, wherein heads=0 and tails=1. I could cover my desk with coins and arrange them into groups to emulate ascii. I could spell out some message, or record some information. But the pennies are physical things, IMHO the information is just a “pattern” of some aspect of those physical things.
I have a problem: I am afraid that erasing or swiping is false play as it requires the use /input of energy that is not generated endogenously.
The Wikipedia link says that Szilard argued that the physical process by which Maxwell’s demon acts itself creates entropy. The entropy of the box alone decreases but the total entropy of the Demon/box system does not. The Landauer principle arose because there are reversible, that is entropy-conserving, ways to separate the particles, whatever they may be. But even these processes requires information destruction that increases entropy. The objection is that this is a consequent of the second law of thermodynamics, not an independent derivation. (I see no problem there, but I’m a materialist who thinks science corrigibly describes reality.)
So far, so good I hope. The first thing is, I don’t understand what information would need to be recorded, other than the average KE. I’ve got a guess, but more below. The second thing is, what ever continual stream of data must be recorded, I don’t understand why this isn’t deemed a physical process that is an intrinsic part of the demon/box system.
And my obtuseness extends even further. I imagine the box to be small as a bacterium. The same processes that cause Brownian motion by unequal impacts from particles will take place. As near as I can deduce, this will happen both within and without the box. I think the impacts in the high KE part of the box will cause an irregular variation in rotation and add to the Brownian vibration. If this is correct, is this an increase in entropy?
I’m sure the box is posited to be constructed of a material that will not deform under the different pressures. But the barrier must eventually be in thermal equilibrium with the two different compartments of the box, as a frying pan handle must have two different temperatures, one at the pan and one by your hand. I think the handle is not always in equilibrium and when if it is, loss of heat to the air etc. plays a role. But that can’t be a part of the Maxwell’s demon setup. If we think of the different KEs and the positions of the particles in the barrier as information, do we think of the gradient from the cold side to the hot side as a loss of information due to increased uncertainty? Obviously this is my guess as to what Landauer could have meant.
Yes, it seems information is in a sense in the eye of the beholder. For something to be regarded as “information” it must be interpreted as such. Can any “information” be understood as simply objectively there? If not, there is an inherent subjectivity in regarding certain patterns as “information” whereas the world described by physical law is manifestly objective. In this light Landauer’s principle may provide another intriguing glimpse into the objective/subjective divide that we seem to come face to face with when thinking about what quantum mechanics means.
How does Landauer’s principle relate to the black hole information paradox, if at all? If matter falls into a black hole and information is lost to the rest of the universe, should there not be a compensating rise in heat (entropy)? Hawking radiation?
Barring quantum weirdness, there is no irreversible loss of information, is there? Can’t we always run the film backwards? It might not be convenient to do so (I’d rather not follow all those molecular collisions backwards to reconstruct the events of that morning fifty years ago and find out who really killed JFK) but it is always possible in principle.
I’ve also never really gotten my head around Maxwell’s demon. Even if erasing the information is such a big deal, can’t we stipulate that the demon’s information processing hardware is arbitrarily fine, dwarfed by the relative boulders that are the molecules in the chambers? Then the demon has decreased entropy massively in the form of the segregated molecules, compared to the tiny extent to which he has increased it by erasing or not erasing information in his own information processing machinery, and the thought experiment still goes through.
Finally, the single molecule in the piston – isn’t the second law a law of statistics, of aggregates? Haven’t you kind of exceeded the second law’s domain of applicability as soon as you restrict yourself to a single molecule? With only one molecule, can you even say that the system is in a state of maximum entropy?
I’ve always been suspicious about the ontological status of information. I think that sometimes people go too far with the highly suggestive correspondences between information and thermodynamics. Information, ones and zeros, are Platonic abstractions, like Euclidean points and planes.
The above notwithstanding, it’s not false modesty when I say that I don’t completely understand all the issues and arguments here.
-John Gregg
How does “loss” ( or “erasure”) of information in the context of Maxwell’s demon tie in with the claim by certain black hole warriors (Susskind, etc.) that information is never lost?
In regard to the Toyobe experiment:
“Physicists in Japan have shown experimentally that a particle can be made to do work simply by receiving information, rather than energy.”
It seems to be something like a demonstration of Maxwell’s Demon.
http://physicsworld.com/cws/article/…rted-to-energy
My question is:
Can the conversion of information into energy work in reverse? In other words, can energy be converted to information? How would that work? Does it actually happen?
“But the Demon has to somehow keep track of what its measurements have revealed. And unless it has an infinitely big notebook, it’s going to eventually have to erase some of its records about the outcomes of those measurements — and that’s the truly irreversible process. ” – not sure that I follow this, must have missed something. The Demon only has to keep track of the average of the speed of the particles he sees and let the faster ones through and the slower ones are sent back. He doesn’t need an infinitely big notebook for that?
I was a little surprised not to see more of a link to quantum computing.
As I understand it, the only irreversible process required for a computation is storing the result. In particular, data can be copied irreversibly as long as it is copied to a cell with a fixed initial state. Thus, to save the result one must clear a memory cell (from a random initial state to a known state such as 0) and this the only process in the computation that must increase entropy–in theory, in practice any device of human manufacture, even a quantum computer, is going to increase entropy all over the place 🙂
This brings up an interesting connection between memory and entropy increase that has implications for the arrow of time. We remember the past and not the future because the very act of memory formation increases entropy. A system that remembers an event added entropy to the universe to create that memory.
Some of this is discussed in an engaging and laymen-friendly way in this book:
Feynman Lectures on Computation
Pingback: Maxwell’s Demon always adds energy | The Furloff
Just an analysis that reveals the tautological nature of Landauer’s principle.
http://thefurloff.com/2013/12/01/maxwells-demon-always-adds-energy/
Sean,
Thanks for your and Jennifer’s efforts to expand knowledge and awareness, to reduce ignorance and nonsense, by sharing the wonders of our natural world. And thanks for doing so with such great clarity, expressiveness, and care.
As Charles McCabe said, “Any clod can have the facts, but having opinions is an art.” Powerful expression is the key: Anyone can be factually correct but still lose an argument, or fail to be persuasive, by being unable to express themselves or by failing to understand their audience or the sources of differences of opinion or belief.
The most important first step is to start from a place of shared understanding or perspective or experience. And that, of all your and Jennifer’s combined talents, is the one I appreciate most. Be it anti-de Sitter space or atheism, you always start by first understanding your audience and engaging with them.
Engaging with passion, a passion that typically evokes shared curiosity. Be it passion for science, philosophy, people, places, or just life and living. (Speaking of life and living, I especially enjoyed Jennifer’s story describing the path leading to this image.)
I am very thankful for all that one of science’s true “power couples” has shared, and eagerly look forward to what the future brings. Jennifer’s blog led me to yours: Both are valuable gifts that keep on giving.
Best Wishes for the Holidays and the New Year,
– Bob Cunningham
Hal: that was an interesting read. I’m reminded of the -13.6eV hydrogen ground state binding energy, which has been likened to “a bigger box” for the electron wavefunction. Follow the link to atomic orbitals and note that electrons “exist as standing waves”.
John Duffield –
I think your example with the arrangement of coins on a desk can be used as a good illustration of this principle.
Consider: Suppose you arrange the coins in such a way to spell out a word in ASCII or perform some binary computation or emulate the human genome. By my reckoning, you are right in saying that the information content has to do with the pattern, and depending on what patterns you are looking for, you might get different measures of information. But say you pick a particular measure for the information and stick with it (iirc this is referred to by physicists as “coarse graining.”)
So now some toddler comes over and knocks the thing over, simultaneously destroying the information and increasing the entropy.