Thanksgiving

 This year we give thanks for a feature of nature that is frequently misunderstood: quanta. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, the Fourier Transform, Riemannian Geometry, the speed of light, the Jarzynski equality, the moons of Jupiter, space, black hole entropy, electromagnetism, and Arrow’s Impossibility Theorem.)

Of course quantum mechanics is very important and somewhat misunderstood in its own right; I can recommend a good book if you’d like to learn more. But we’re not getting into the measurement problem or the reality problem just now. I want to highlight one particular feature of quantum mechanics that is sometimes misinterpreted: the fact that some things, like individual excitations of quantized fields (“particles”) or the energy levels of atoms, come in sets of discrete numbers, rather than taking values on a smooth continuum. These discrete chunks of something-or-other are the “quanta” being referred to in the title of a different book, scheduled to come out next spring.

The basic issue is that people hear the phrase “quantum mechanics,” or even take a course in it, and come away with the impression that reality is somehow pixelized — made up of smallest possible units — rather than being ultimately smooth and continuous. That’s not right! Quantum theory, as far as it is currently understood, is all about smoothness. The lumpiness of “quanta” is just apparent, although it’s a very important appearance.

What’s actually happening is a combination of (1) fundamentally smooth functions, (2) differential equations, (3) boundary conditions, and (4) what we care about.

This might sound confusing, so let’s fix ideas by looking at a ubiquitous example: the simple harmonic oscillator. That can be thought of as a particle moving in one dimension, x, with a potential energy that looks like a parabola: . In classical mechanics, there is a lowest-energy state where the particle just sits at the bottom of its potential, unmoving, so both its kinetic and potential energies are zero. We can give it any positive amount of energy we like, either by kicking it to impart motion or just picking it up and dropping it in the potential at some point other than the origin.

Quantum mechanically, that’s not quite true (although it’s truer than you might think). Now we have a set of discrete energy levels, starting from the ground state and going upward in equal increments. Quanta!

But we didn’t put the quanta in. They come out of the above four ingredients. First, the particle is described not by its position and momentum, but by its wave function, . Nothing discrete about that; it’s a fundamentally smooth function. But second, that function isn’t arbitrary; it’s going to obey the Schrödinger equation, which is a special differential equation. The Schrödinger equation tells us how the wave function evolves with time, and we can solve it starting with any initial wave function we like. Still nothing discrete there. But there is one requirement, coming from the idea of boundary conditions: if the wave function grows (or remains constant) as , the potential energy grows along with it. (It actually has to diminish at infinity just to be a wave function at all, but for the moment let’s think about the energy.) When we bring in the fourth ingredient, “what we care about,” the answer is that we care about low-energy states of the oscillator. That’s because in real-world situations, there is dissipation. Whatever physical system is being modeled by the harmonic oscillator, in reality it will most likely have friction or be able to give off photons or something like that. So no matter where we start, left to its own devices the oscillator will diminish in energy. So we generally care about states with relatively low energy.

Since this is quantum mechanics after all, most states of the wave function won’t have a definite energy, in much the same way they will not have a definite position or momentum. (They have “an energy” — the expectation value of the Hamiltonian — but not a “definite” one, since you won’t necessarily observe that value.) But there are some special states, the energy eigenstates, associated with a specific, measurable amount of energy. It is those states that are discrete: they come in a set made of a lowest-energy “ground” state, plus a ladder of evenly-spaced states of ever-higher energy.

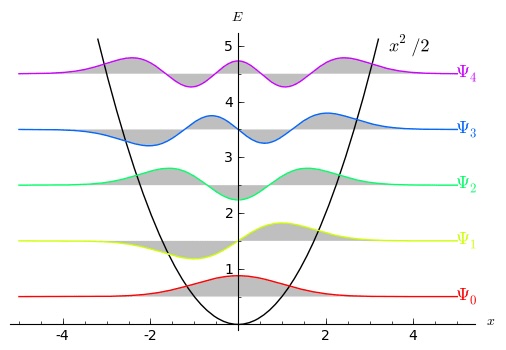
We can even see why that’s true, and why the states look the way they do, just by thinking about boundary conditions. Since each state has finite energy, the wave function has to be zero at the far left and also at the far right. The energy in the state comes from two sources: the potential, and the “gradient” energy from the wiggles in the wave function. The lowest-energy state will be a compromise between “staying as close to as possible” and “not changing too rapidly at any point.” That compromise looks like the bottom (red) curve in the figure: starts at zero on the left, gradually increases and then decreases as it continues on to the right. It is a feature of eigenstates that they are all “orthogonal” to each other — there is zero net overlap between them. (Technically, if you multiply them together and integrate over , the answer is zero.) So the next eigenstate will first oscillate down, then up, then back to zero. Subsequent energy eigenstates will each oscillate just a bit more, so they contain the least possible energy while being orthogonal to all the lower-lying states. Those requirements mean that they will each pass through zero exactly one more time than the state just below them.

And that is where the “quantum” nature of quantum mechanics comes from. Not from fundamental discreteness or anything like that; just from the properties of the set of solutions to a perfectly smooth differential equation. It’s precisely the same as why you get a fundamental note from a violin string tied at both ends, as well as a series of discrete harmonics, even though the string itself is perfectly smooth.

One cool aspect of this is that it also explains why quantum fields look like particles. A field is essentially the opposite of a particle: the latter has a specific location, while the former is spread all throughout space. But quantum fields solve equations with boundary conditions, and we care about the solutions. It turns out (see above-advertised book for details!) that if you look carefully at just a single “mode” of a field — a plane-wave vibration with specified wavelength — its wave function behaves much like that of a simple harmonic oscillator. That is, there is a ground state, a first excited state, a second excited state, and so on. Through a bit of investigation, we can verify that these states look and act like a state with zero particles, one particle, two particles, and so on. That’s where particles come from.

We see particles in the world, not because it is fundamentally lumpy, but because it is fundamentally smooth, while obeying equations with certain boundary conditions. It’s always tempting to take what we see to be the underlying truth of nature, but quantum mechanics warns us not to give in.

Is reality fundamentally discrete? Nobody knows. Quantum mechanics is certainly not, even if you have quantum gravity. Nothing we know about gravity implies that “spacetime is discrete at the Planck scale.” (That may be true, but it is not implied by anything we currently know; indeed, it is counter-indicated by things like the holographic principle.) You can think of the Planck length as the scale at which the classical approximation to spacetime is likely to break down, but that’s a statement about our approximation schemes, not the fundamental nature of reality.

States in quantum theory are described by rays in Hilbert space, which is a vector space, and vector spaces are completely smooth. You can construct a candidate vector space by starting with some discrete things like bits, then considering linear combinations, as happens in quantum computing (qubits) or various discretized models of spacetime. The resulting Hilbert space is finite-dimensional, but is still itself very much smooth, not discrete. (Rough guide: “quantizing” a discrete system gets you a finite-dimensional Hilbert space, quantizing a smooth system gets you an infinite-dimensional Hilbert space.) True discreteness requires throwing out ordinary quantum mechanics and replacing it with something fundamentally discrete, hoping that conventional QM emerges in some limit. That’s the approach followed, for example, in models like the Wolfram Physics Project. I recently wrote a paper proposing a judicious compromise, where standard QM is modified in the mildest possible way, replacing evolution in a smooth Hilbert space with evolution on a discrete lattice defined on a torus. It raises some cosmological worries, but might otherwise be phenomenologically acceptable. I don’t yet know if it has any specific experimental consequences, but we’re thinking about that.