Major announcement coming!
[Update: Of course by now the announcement has come, of the discovery of signatures of gravitational waves in the cosmic microwave background by the BICEP2 experiment, more or less as the post below surmised. This follow-up post features the main result plots from the announcement.]
That much is clear, from this press release: on Monday at noon Eastern time, astronomers will “announce a major discovery.” No evidence from that page what the discovery actually is. But if you’re friends with a lot of cosmologists on Facebook/Twitter (or if you just read the Guardian), you’ve heard the rumor: the BICEP2 experiment has purportedly detected signs of gravitational waves in the polarization of the cosmic microwave background radiation. If it’s true (and the result holds up), it will be an enormously important clue about what happened at the very earliest moments of the Big Bang. Normally I wouldn’t be spreading rumors, but once it’s in the newspapers, I figure why not? And in the meantime we can think about what such a discovery would mean, regardless of what the announcement actually turns out to be (and whether the result holds up). See also Richard Easther, Résonaances, Sesh Nadathur, Philip Gibbs, Shaun Hotchkiss, and Peter Coles. At a slightly more technical level, Daniel Baumann has a slide-show review.
Punchline: other than finding life on other planets or directly detecting dark matter, I can’t think of any other plausible near-term astrophysical discovery more important than this one for improving our understanding of the universe. It would be the biggest thing since dark energy. (And I might owe Max Tegmark $100 — at least, if Planck confirms the result. I will joyfully pay up.) Note that the big news here isn’t that gravitational waves exist — of course they do. The big news is that we have experimental evidence of something that was happening right when our universe was being born.

Cosmic inflation is actually a pretty simple idea. Very early on–we’re not sure exactly when, but plausibly 10-35 seconds or less after the Planck time–the universe went through a phase of accelerated expansion for some reason or another. There are many models for what could have caused such a phase; sorting them out is exactly what we’re trying to do here. The basic effect of this inflationary era is to smooth things out: stuff like density perturbations, spatial curvature, and unwanted relics just get diluted away. Then at some point–again, we aren’t sure when or why–this period ends, and the energy that was driving the accelerated expansion converts into ordinary matter and radiation, and the conventional Hot Big Bang story begins.
Except that quantum mechanics says that we can’t completely smooth things out. The Heisenberg uncertainty principle tells us that there will always be an irreducible minimum amount of jiggle in any quantum system, even when it’s in its lowest-energy (“vacuum”) state. In the context of inflation, that means that quantum fields that are relatively light (low mass) will exhibit fluctuations. (Gauge fields like photons are an exception, due to symmetries that we don’t need to go into right now.)
So inflation makes certain crude predictions, which have come true: the universe is roughly homogeneous, and the curvature of space is very small. But the perturbations on top of this basic smoothness provide more specific, quantitative information, and offer more tangible hope of learning more about the inflationary era (including whether inflation happened at all).
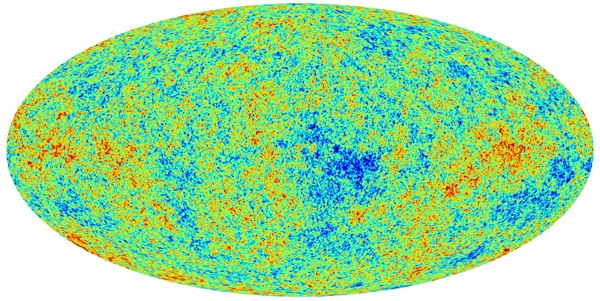
There are two types of perturbations we expect to see, based on two kinds of light quantum fields that fluctuated during inflation: the “inflaton” field itself, and the gravitational field. We don’t know what field it is that drove inflation, so we just call it the “inflaton” and try to determine its properties from observation. It’s the inflaton that eventually converts into matter and radiation, so the inflaton fluctuations produce fluctuations in the density of the early plasma (sometimes called “scalar” fluctuations). These are what we have already seen in the Cosmic Microwave Background (CMB), the leftover radiation from the Big Bang. Maps like this one from the Planck satellite show differences in temperature from point to point in the CMB, and it’s these small difference (about one part in 105) that grow into stars, galaxies and clusters as the universe expands.
Then, of course, there are quantum fluctuations in the gravitational field: gravitational waves, or “gravitons” if you prefer speaking quantum-mechanically (sometimes called “tensor” fluctuations in contrast with “scalar” density fluctuations). It was in the early 80’s, soon after inflation itself came along, that several groups pointed out this prediction: Rubakov, Sazhin, and Veryaskin; Fabbri and Pollock; and Abbott and Wise. [Update: As Alessandra Buonanno points out in the comments, the idea that gravitational waves could be generated by quantum fluctuations in an expanding universe was investigated earlier by L. Grishchuk, Sov. Phys. JETP 40, 409 (1975), and A. Starobinsky, JETP Lett. 30, 682 (1979). Grishchuk was before inflation was invented, so the resulting wavelengths would have been much shorter (and unobservable in the CMB), but it’s the same underlying physics; Starobinsky actually had is own proto-inflationary model.] Just as an electromagnetic wave is an oscillation in the electric and magnetic fields that propagates at the speed of light, a gravitational wave is an oscillation in the gravitational field that propagates at the speed of light. We can detect electromagnetic waves because they would cause a charged particle to jiggle up and down; we could (in principle, though not yet in practice) detect gravitational waves because they alternately stretch things apart and then compress them together as they pass.
Gravitational waves from inflation are interesting for a couple of reasons. First, we know they should be there; gravitation certainly exists, and it’s a massless field. Second, there is a way to disentangle the gravitational waves from the density fluctuations, using the polarization of the CMB. This was noted in a flurry of papers from 1996 by different subsets of Seljak, Zaldarriaga, Kamionkowski, Kosowsky, and Stebbins: 1, 2, 3, 4, 5. Finally, how strong the gravitational waves are at different wavelengths reveals a great deal about the details of inflation — including one magic number, the energy density of the universe during the inflationary era.
Any kind of electromagnetic radiation, such as the microwaves we observe in the CMB, has a polarization. An electromagnetic wave is just a propagating ripple in the electric and magnetic fields, and we (somewhat arbitrarily) define the direction of polarization to be the direction in which the electric field is oscillating up and down. Of course when we observe many photons, the polarizations of each photon will often be pointing in random directions, giving a net effect that adds up nearly to zero. That’s the case in an ordinary incandescent bulb, and it’s almost the case for the CMB. But not quite. There is a tiny amount of residual polarization in the CMB, first discovered by the DASI telescope. (I helped organize the talk at the Cosmo-02 where the discovery of CMB polarization was announced. It was the Ph.D. thesis project for John Kovac, who is now on the faculty at Harvard and the PI on BICEP. I can brag that he took my cosmology class back in grad school.)
But there’s polarization, and there’s polarization. Even without any gravitational waves, the CMB would still be polarized, just due to the distortions brought about by ordinary density perturbations. That’s what DASI discovered. Happily, we can distinguish density-induced polarization (“scalar modes”) from gravitational-wave-induced polarization (“tensor modes”) by the shape of the polarization pattern on the sky.
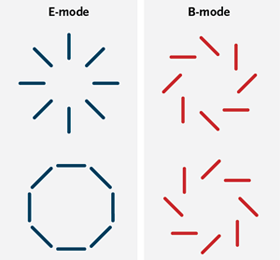 A map of CMB polarization takes the form of little line segments on the sky — the direction of the net oscillation in the electric field. If you just have polarization at one point, that’s all the information available; but if you have a map of polarization over some area, you can decompose it into what are called E-modes and B-modes. (See this nice article from Sky & Telescope.) The difference is that B-modes have a net twist to them as you travel around in a circle. That sounds a little loosey-goosey, but there is a careful mathematical way of distinguishing between the two kinds.
A map of CMB polarization takes the form of little line segments on the sky — the direction of the net oscillation in the electric field. If you just have polarization at one point, that’s all the information available; but if you have a map of polarization over some area, you can decompose it into what are called E-modes and B-modes. (See this nice article from Sky & Telescope.) The difference is that B-modes have a net twist to them as you travel around in a circle. That sounds a little loosey-goosey, but there is a careful mathematical way of distinguishing between the two kinds.
Very roughly: density (scalar, inflaton) perturbations produce only E-mode polarization, whereas gravitational wave (tensor) perturbations produce B-mode polarization as well as E-modes. [Update: Thanks to asad and Daniel in comments for a correction here.] That’s why looking for the B-modes is such a big deal.
It’s also hard, for a number of reasons. When we said “very roughly,” we meant it — there are various effects other than gravity waves that can create B-modes, typically by taking some E-modes and messing with them. One such effect is gravitational lensing — the deflection of light by matter in between us and the CMB. Indeed, B-modes from lensing have already been detected twice, by the South Pole Telescope and by the PolarBEAR experiment.
But now the rumor is that the BICEP2 experiment has found a signature of honest-to-goodness B-modes from primordial gravitational waves. I won’t speculate about the details like the amplitude or the statistical significance, since we’ll find that out soon enough.
Let’s instead think just a little bit about what it would mean. Both density perturbations and gravitational-wave perturbations arise from quantum fluctuations generated during inflation, and the amount of perturbation depends on the energy scale E at which inflation happens, defined as the energy density to the 1/4 power. (I’m presuming here that inflation is the right story, but of course we don’t know that for sure.) But there’s a difference: for density perturbations, what actually fluctuates is some hypothetical inflaton field ϕ. That’s related to the energy density, but it’s not exactly the same thing; the actual density comes from the potential energy, V(ϕ). So measuring the density fluctuations (which we’ve done) doesn’t tell us the energy scale of inflation directly; it’s modulated by the unknown function V(ϕ). The flatter the potential, the larger the density perturbations. We can make educated guesses, which tend to put the energy scale E at around 1016 GeV (where a GeV is a billion electron volts, about the mass of the proton). That’s pretty darn close to the Planck scale of 1018 GeV, and basically equal to the scale of hypothetical grand unification, so you see why any empirical information we can get about physics at those scales is extremely interesting indeed.
Gravitational-wave perturbations are different. They are not modulated by some unknown potential; they are produced by inflation, and we observe them directly. In straightforward models of inflation, the amplitude of the gravitational waves is directly proportional to the inflationary energy scale. If this rumored measurement (and the inflationary interpretation) are correct, we would have data about a physical process just a bit below the Planck scale. Currently, our empirical knowledge of the early universe only stretches to about one second after the Big Bang, courtesy of primordial nucleosynthesis. Here we’re talking about pushing that to less than 10-35 seconds.
Now to get a bit quantitative. We can approximately describe a set of cosmological perturbations by two numbers: the overall amplitude A, and the “spectral index” or “tilt” n that tells you how the perturbations change from large wavelengths to shorter wavelengths. For the density perturbations, we have a fairly good handle on what these numbers are; the amplitude is about 10-5, and the spectral index is about 0.96. For historical reasons, density perturbations that are the same on all wavelengths are said to have nS = 1, while gravitational perturbations that are the same on all wavelengths are said to have nT = 0, where S is for “scalar” and T is for “tensor.” (I think it’s conceivable that the data are still compatible with nS = 1 rather than 0.96, but you really have to bend over backwards.) Finally, we often compare the gravitational-wave perturbations to the density perturbations by giving the ratio r = AT/AS of amplitudes (tensor divided by scalar).
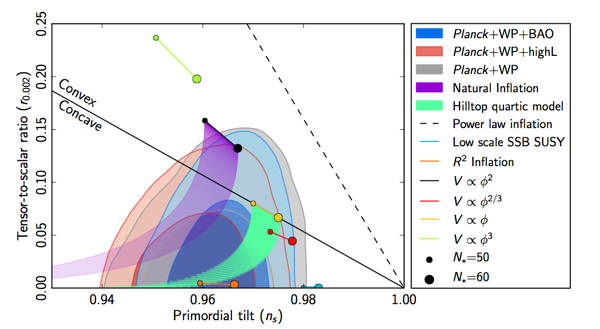
Here are the best constraints as of Sunday March 16, 2014, from the Planck satellite. Horizontal axis is the tilt of the density perturbations, vertical axis is the ratio of gravitational-wave to density fluctuations. (Note that Planck hasn’t yet released polarization data, but even just the temperature fluctuations provide some constraints on the gravitational-wave amplitude.) The half-ellipse blobs at the bottom are the regions allowed by the data, and the various dots and lines are the predictions of different inflationary models.
So you see that pre-BICEP2, we’re quite comfortable with density perturbations that have a spectral index nS = 0.96 or so, and no tensor fluctuations at all (r = 0). From what I’m told, the only way BICEP should be able to get a really solid detection (five sigma) is if r is about 0.2. Which seems to be in a bit of tension with the limits plotted here (although admittedly they are only two-sigma error contours). But we don’t know yet, and there is a bit of room for slop; maybe the central value found by BICEP2 is around 0.2, but it’s consistent with 0.1, which would be perfectly fine.
What does it all mean? Most importantly, a gravitational-wave signal that big is … really big. It corresponds to an energy scale during inflation that is pretty darn high. It’s actually not so easy (although certainly possible) to come up with models that have such prominent gravitational waves. This goes back to something called the Lyth bound, after its discoverer David Lyth. The issue is that there is an interplay between the size of the density perturbations, the size of the gravitational-wave perturbations, and the total amount by which the inflaton field rolls during inflation. Very roughly, the amount of field rolling (in units of the Planck scale) is ten times the square root of r. So if r > 0.01, the inflaton ϕ rolled by more than the Planck scale during inflation. That’s not impossible — it’s just provocative. In string theory, for example, most candidates for the inflaton are periodic, with a period of about the Planck scale. [Update: at least, that’s been the conventional wisdom in certain quarters. See comment by Eva below.] So large r is hard to get. And r=0.2 is large indeed.
There are loopholes, of course. An intriguing one is axion monodromy inflation, which has been investigated by Eva Silverstein, Alexander Westphal, and Liam McAllister. Instead of having just one periodic field, they imagine multi-dimensional field spaces; then the inflaton can essentially wind around one direction several times before reaching the bottom of its potential, allowing for quite large effective field values.
More importantly than the prospects for any given model, however, this is great news for inflation itself. While it’s the starting point for much contemporary cosmological theorizing about the early universe, honest physicists are quick to admit that inflation has its conceptual problems. The prediction of gravitational waves is one of the strongest empirical handles we have on whether inflation actually happened, so if this result is announced like the rumors say (and it holds up) it will dramatically effect how we think about the earliest moments in the history of our universe. And if we succeed in measuring not only the amplitude of the gravitational waves but also their spectral index nT, there is a “consistency relation” that holds in simple models of inflation: r = -8nT. If that turns out to hold, it will be very hard indeed to deny that inflation happened. (Sadly, there are all sorts of non-simple models of inflation in which the consistency relation is violated, so if it doesn’t turn out to hold, we won’t really know one way or the other.)
There is always the possibility that a result is announced but it doesn’t hold up, of course. These are really hard measurements, with many ways to go wrong, even for experimenters as undoubtedly careful as the BICEP folks are. When the announcement is made, look not only for the claimed statistical significance, but also (as Eiichiro Komatsu has emphasized) for its robustness — does it show up in multiple frequencies (of radiation), as well as at multiple scales on the sky? Happily there are many competing experiments that will move very quickly to tell us whether this is on the right track. Science!
Updates soon. Very soon.
Pingback: Primordial Gravitational Waves? | viXra log
That’s probably the most comprehensive and readable summary of the BICEP2 discovery I’ve read so far – thanks for posting it!
I’m a little puzzled though – if this is such a MAJOR discovery, why was there not so much excitement about the possibilities of the soon to be announced Planck polarisation results? Surely people realised primordial gravitational waves could also be found by Planck – so why so little excitement about the possibility of their discovery (at least I didn’t notice much hype on blogs, which I would have expected if , like now, Harvard are claiming a MAJOR discovery (and apparently inviting Guth and Linde to the announcement tomorrow))?
As you know, it would be more correct to say that density perturbations produce only E-mode polarization, whereas gravitational wave (tensor) perturbations produce both E- and B-mode polarization. Your phrasing implies that gravitational waves only produce B.
Great post Sean. One or two comments — Tensor perturbations produce *BOTH* E and B-Modes, but B-modes are the smoking gun because they can’t be produced by scalar perturbations. Also, independent of the inflationary story, there was also the seminal paper of Polnarev noting the possibility of polarizing the CMB with a background of gravitational waves, http://adsabs.harvard.edu/abs/1985SvA….29..607P.
Of course he did not make the connection between tensors and B (curl)-modes, but its still an important part of the story IMHO.
James — I think everyone thought that existing limits on $r$ were too low to make a discovery possible with Planck. Not sure if that will now change, though there are known issues with low-l Planck polarization (first polarization data release is rumored to only be high-l). Now the question is how you hide such a high $r$ in the temperature data — this would seem to require fairly large running of the scalar spectral index, which is hard to explain in slow-roll single field inflation.
Thanks Daniel,
so this is a really unexpected gem of an observation by BICEP2 (if correct!)
asad and Daniel– You’re right, that’s misleading; I’ll fix it.
James– Most of us were expecting limits from Planck — that’s why I made my bet with Max!
Thanks for a great summary! If this turns out to be robust detection, I’ll have to add some more material to the “evidence for GWs” section of my thesis…
I’m not a physicist, but I’ll bet you’re right. About 6 months ago new news articles on the subject started getting hard to find. Before that if someone sneezed while talking about gravitational waves it made it into an article.
Pingback: Allgemeines Live-Blog ab dem 16. März 2014 | Skyweek Zwei Punkt Null
Hi Sean,
Great summary of this amazing physics, capturing all the different facets of the subject. Just one pedantic comment about the issue of large-field inflation in string theory.
I don’t think we have a statement that most candidate inflatons are small field. Axion fields are generically lifted by monodromy (they are not periodic on a given branch of their potential, despite the underlying shift symmetry) in the presence of the fluxes and branes of string theory. This is true individually, and also for multiple fields (there is a previous idea known as N flation using multiple axions to obtain an effectively large range — this has a very red tilt, but maybe the most generic idea is multiple axions taking into account their monodromy). Now axion fields and their duals are an order one (or better) fraction of the scalar fields in string theory. In SUSY regimes, they are roughly half the fields, and in higher-dimensional starting points their number actually grows exponentially (like 2^D), dominating the spectrum. There is lore in the community that small field is more common, but I don’t get that. (The number of papers on it may be larger, but of course that’s a very different statement…).
Andrew would be pleased =)
Eva– Point taken. Small-field models are favored by conventional wisdom, but not by an actual reliable argument; I’ll update the post to reflect that.
Sean, you maybe missed one article in your list of blogs that have written about this
😉
More importantly, if this is truly a measurement of r=0.2, at l~100, then what Daniel pointed out is important. This will be indicating a large running of the scalar spectral index. This is something that models like “Axion Monodromy”, “Natural inflation”, “m^2\phi^2”, etc aren’t so keen to produce. It would also be implying that the (anomalous) deficit in scalar power on large scales is even more drastic than previously suspected.
Shaun– sorry, I actually did have your blog post open in a tab, but somehow didn’t include it. Until now!
Hi Sean , thanks for the great post.
Robert H. Brandenberger had an interesting paper a few years ago saying that B modes were not unique to inflation:
http://arxiv.org/pdf/1104.3581.pdf
the real test would be ( if i understood the paper properly) to see if the gravity wave spectrum was red or blue titled. Do you think that a ground based experiment could determine this ?
I note that on PRISM site they claim any ground based detection will need to confirmed from space and only a space based detector can get the required information.
http://www.prism-mission.org/documents/prism_questions_and_answers.pdf
love to hear your thoughts on this Sean.
Hi Sean,
nice summary.
“It was in the early 80′s, soon after inflation itself came along, that several groups pointed out this prediction: Rubakov, Sazhin, and Veryaskin; Fabbri and Pollock; and Abbott and Wise.”
As far as I know the first papers discussing it are in the 70s by L. Grishchuk, Sov. Phys. JETP 40, 409 (1974), and A. Starobinsky JETP Lett. 30, 682 (1979) [http://www.jetpletters.ac.ru/ps/1370/article_20738.pdf].
Alessandra– Thanks, I don’t know those papers (and I don’t have access to them at the moment). Did they really predict gravitational waves from inflation before inflation had been invented? (Would seem like a typical Russian thing to do.)
And Bruce would have been tickled too. I hope it is indeed a “robust” result. Thanks, Sean, for such a clear explanation too.
The key mechanism responsible of the production of gravitational waves during inflation is the amplification of quantum vacuum fluctuations, which is a very general mechanism in quantum-field theory in curved space-time. It was first discussed in cosmology in those papers.
I don’t understand a shit
but this is big
Pingback: BICEP2 Updates | Sean Carroll
Sean, love the post.
Can you say that if primordial B-modes are found then inflation did happen?
Are there other ways to achieve such B-modes (not the lensed B-modes, but true primordial B-modes)?
If there are no primordial B-modes found (at whatever limits BICEP2 might have), would this be an indication that inflation did not happen?
Just a note of thanks for keeping us abreast of the latest in cosmology. Exciting times!
(phil h – just this moment saw your link to the Brandenberger paper – maybe that will answer my questions, the abstract looks very good!)