There’s no question that quantum fluctuations play a crucial role in modern cosmology, as the recent BICEP2 observations have reminded us. According to inflation, all of the structures we see in the universe, from galaxies up to superclusters and beyond, originated as tiny quantum fluctuations in the very early universe, as did the gravitational waves seen by BICEP2. But quantum fluctuations are a bit of a mixed blessing: in addition to providing an origin for density perturbations and gravitational waves (good!), they are also supposed to give rise to Boltzmann brains (bad) and eternal inflation (good or bad, depending on taste). Nobody would deny that it behooves cosmologists to understand quantum fluctuations as well as they can, especially since our theories involve mysterious aspects of physics operating at absurdly high energies.
Kim Boddy, Jason Pollack and I have been re-examining how quantum fluctuations work in cosmology, and in a new paper we’ve come to a surprising conclusion: cosmologists have been getting it wrong for decades now. In an expanding universe that has nothing in it but vacuum energy, there simply aren’t any quantum fluctuations at all. Our approach shows that the conventional understanding of inflationary perturbations gets the right answer, although the perturbations aren’t due to “fluctuations”; they’re due to an effective measurement of the quantum state of the inflaton field when the universe reheats at the end of inflation. In contrast, less empirically-grounded ideas such as Boltzmann brains and eternal inflation both rely crucially on treating fluctuations as true dynamical events, occurring in real time — and we say that’s just wrong.
All very dramatically at odds with the conventional wisdom, if we’re right. Which means, of course, that there’s always a chance we’re wrong (although we don’t think it’s a big chance). This paper is pretty conceptual, which a skeptic might take as a euphemism for “hand-waving”; we’re planning on digging into some of the mathematical details in future work, but for the time being our paper should be mostly understandable to anyone who knows undergraduate quantum mechanics. Here’s the abstract:
De Sitter Space Without Quantum Fluctuations
Kimberly K. Boddy, Sean M. Carroll, and Jason PollackWe argue that, under certain plausible assumptions, de Sitter space settles into a quiescent vacuum in which there are no quantum fluctuations. Quantum fluctuations require time-dependent histories of out-of-equilibrium recording devices, which are absent in stationary states. For a massive scalar field in a fixed de Sitter background, the cosmic no-hair theorem implies that the state of the patch approaches the vacuum, where there are no fluctuations. We argue that an analogous conclusion holds whenever a patch of de Sitter is embedded in a larger theory with an infinite-dimensional Hilbert space, including semiclassical quantum gravity with false vacua or complementarity in theories with at least one Minkowski vacuum. This reasoning provides an escape from the Boltzmann brain problem in such theories. It also implies that vacuum states do not uptunnel to higher-energy vacua and that perturbations do not decohere while slow-roll inflation occurs, suggesting that eternal inflation is much less common than often supposed. On the other hand, if a de Sitter patch is a closed system with a finite-dimensional Hilbert space, there will be Poincaré recurrences and Boltzmann fluctuations into lower-entropy states. Our analysis does not alter the conventional understanding of the origin of density fluctuations from primordial inflation, since reheating naturally generates a high-entropy environment and leads to decoherence.
The basic idea is simple: what we call “quantum fluctuations” aren’t true, dynamical events that occur in isolated quantum systems. Rather, they are a poetic way of describing the fact that when we observe such systems, the outcomes are randomly distributed rather than deterministically predictable. But when we’re not looking, a system in its ground state (like an electron in its lowest-energy orbital around an atomic nucleus) isn’t fluctuating at all; it’s just sitting there. And in de Sitter space — empty space with a positive cosmological constant — all of the fields are in their ground states. If we were to probe empty de Sitter space with a particle detector, it would certainly detect particles — but there are no particle detectors around, so in fact the quantum fields are sitting there quietly in a stationary state with no definite particle number. Therefore, these kinds of fluctuations aren’t “really happening.”
To get into a bit more detail, there are two things going on here: a certain interpretation on the meaning of “quantum fluctuations,” and some claims about de Sitter space. As far as quantum fluctuations are concerned, we readily admit that our analysis relies heavily on the Everett/Many-Worlds formulation of quantum theory. In that view, there is nothing truly random and unpredictable about quantum dynamics. There is only the smooth, unitary evolution of the wave function according to the Schrödinger equation. Apparent unpredictability arises because that smooth evolution can take a quantum state from a single connected “world” into several distinct “branches,” each of which features certain entanglements between subsystems (like the spin of a particle and the readout of a measuring apparatus that just measured that spin). But such branching doesn’t happen willy-nilly; it’s crucial that the system undergoes decoherence. Roughly speaking, that’s when a macroscopic quantum system becomes entangled with an unobserved environment. Macroscopically different states of the system (like different readouts on a measuring apparatus, or alive/dead states of a cat in a box) become entangled with different environment states. Once that happens, the two states of the macroscopic system can never talk to each other again, and in particular cannot experience mutual quantum interference. It’s as if they have become part of two different worlds.
So in the Everett picture, a quantum system in its lowest-energy state (or in any state of precisely-defined energy) isn’t fluctuating at all. It’s just sitting there, until some nosy measuring device comes poking at it. From the point of view of any given observer, the outcome of those pokes is intrinsically random. Because our brains are wired for classical physics, we therefore sometimes speak as if the system is fluctuating around even when we’re not looking at it — as if an electron is actually bouncing around in the vicinity of the nucleus of an atom, and its orbital represents the likelihood of it being in one place or another. But that’s not right: the orbital (the wave function) is the electron, it doesn’t represent our knowledge of it. And when nobody is observing it, literally nothing is fluctuating.
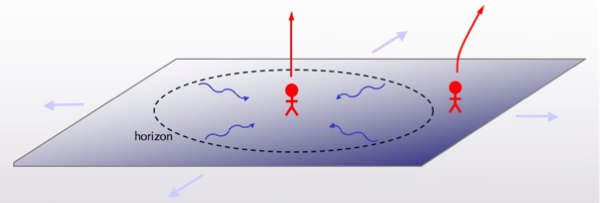
What does this have to do with cosmology? We often contemplate situations in which space is completely empty other than for vacuum energy — perhaps during inflation in the very early universe, or perhaps in our own future once all the matter and radiation has been dispersed by the expansion of the universe. We’re left with de Sitter space. Back in the 70’s, Gibbons and Hawking showed that de Sitter space, just like a black hole, has a temperature. That’s because, just like a black hole, de Sitter space comes with an horizon. That horizon cuts off the degrees of freedom to which any observer has access, leaving them in a thermal state at a well-defined temperature. It’s as if — but, we are claiming, only as if! — the cosmological horizon is radiating into the interior, just as the black hole horizon radiates to the outside world.
But this quantum-mechanical “thermal state” is different from our intuition, once again trained by classical mechanics, of a bunch of particles randomly bouncing around inside a box. Globally (including outside the horizon), the quantum state is static. It only appears thermal to an observer because the horizon cuts them off from the rest of the world. This gives us a mixed state, in which the local observer doesn’t know exactly what state they’re actually in — but all of the allowed possibilities are completely stationary. So once again, nothing is actually fluctuating.
My confidence in this story about quantum fluctuations and de Sitter space is extremely high, even though it does conflict with the way many cosmologists think about the situation. The less secure part of our story is when we move from the idealization of pure de Sitter space to the messy real world. In the real world, you might think you’re in de Sitter space once and for all, but you could actually be in a temporary false-vacuum state. If there is only one vacuum, we can appeal to a “cosmic no-hair theorem” (analogous to similar theorems for black holes) that says a universe with a cosmological constant will eventually dissipate all of its excitations and turn into de Sitter space. But when there are false vacua, the situation is admittedly tricker. We’ve thought about it, and decided that the story we told above for de Sitter space is the one that is usually right, even if you’re in a false vacuum. (There are some subtleties dealing with complementarity and the dimensionality of Hilbert space, but that’s the typical situation.)
The ramifications are very interesting. The idea that Boltzmann brains fluctuate into existence and should count as “observers” in a multiverse cosmology has been a troubling one, and now we’re saying it might not be nearly as severe as people have thought. Whereas before Boltzmann brains were hard to avoid if your cosmological model ever entered a de Sitter phase, now we think it’s quite hard to get them to appear in any appreciable abundance. This might mean that the last paper by Kim and me, asking whether the Higgs field could provide an escape from the BB problem in our actual universe, is addressing a non-problem (in at least some models).
You might worry that our dismissal of quantum fluctuations is too sweeping — after all, don’t we see their effects in the cosmic microwave background? Fortunately, no. The standard story says that the inflaton field undergoes quantum fluctuations, which then get imprinted as fluctuations in density. What we’re saying is that the inflaton doesn’t actually “fluctuate,” it’s just in some calculable quantum state. But there’s nothing “observing” it, causing decoherence and branching of the wave function. At least, not while inflation is going on. But when inflation ends, the universe reheats into a hot plasma of matter and radiation. That actually does lead to decoherence and branching — the microscopic states of the plasma provide an environment that becomes entangled with the large-scale fluctuations of the inflaton, effectively measuring it and collapsing the wave function. So in our picture, all of the textbook predictions for inflation perturbations remain unchanged.
Eternal inflation is a different story. The idea there is that the inflaton field slowly rolls down its potential during inflation, except that quantum fluctuations will occasionally poke the field to go higher rather than lower. When that happens, space expands faster and inflation continues forever. Like Boltzmann brains — and unlike density perturbations — this story relies on the idea that the “fluctuations” are actual events happening in real time, even in the absence of measurement and decoherence. And we’re saying that none of that is true. The field is essentially in a pure state, and simply rolls down its potential. Clearly a lot more careful analysis has to be done here, and we’ve started thinking about it. The stakes are substantial: the fact that inflation is eternal is a key part of its motivation in the minds of many cosmologists. (Note that we’re not saying eternal inflation is impossible; if you are stuck in a false vacuum with a very tiny decay rate, you can stay there for an arbitrarily long time. But the set of models in which inflation is eternal might be much tinier than was previously believed.) As with the Higgs and Boltzmann brains, this might be another case where I am undermining one of my own previous papers. So be it — in science you have to be willing to change your mind when faced with new data or better ideas. (I think that both the Higgs paper and the out-of-equilibrium paper are perfectly correct, given their working assumptions; I just think that the assumptions are much less likely to apply than I used to.)
Finally, it’s interesting to note the role of “interpretations of quantum mechanics” in this story. (I don’t like that term, since we’re not discussing “interpretations,” we’re comparing manifestly different physical theories.) In the Everett formulation, the wave function is a direct reflection of reality; when it is stationary, so is the quantum system. Other approaches take a very different tack. There are formulations of quantum mechanics where collapse of the wave function is truly random and unpredictable; there are others with hidden variables, in which the true state of the universe isn’t defined by the wave function. In any of those cases, our analysis is completely beside the point. It’s interesting to think — but perhaps unsurprising in retrospect — that the correct formulation of quantum mechanics might have crucial implications for the evolution of the universe.
Sean, could you clarify what you mean by “observer” and “observation”? In the informal language you used above, it comes with the implication of a conscious intelligence as an integral part of the process, and I’ll bet that’s not actually the case — or, at least, not in the way it’s commonly understood.
For example: “But that’s not right: the orbital (the wave function) is the electron, it doesn’t represent our knowledge of it. And when nobody is observing it, literally nothing is fluctuating.” That would seem to imply — incorrectly, I’m sure — that the human mind has the power to cause electrons to start fluctuating, merely by focussing one’s attention upon them.
Thanks,
b&
Ben– It has nothing to do with consciousness or intelligence (of course). An “observation” in quantum mechanics happens whenever any out-of-equilibrium macroscopic system becomes entangled with the quantum system being measured. It will then decohere (become entangled with the wider environment), which causes a splitting of the wave function into separate branches.
It’s key that the macroscopic device in question starts out far from equilibrium. Otherwise it would already be entangled with everything, and the measurement/splitting process couldn’t occur.
I haven’t read this yet, just the blog article. Interestingly the idea that quantum fluctuations make no sense absent a measurement process is an idea that has been bandied about on Dr Vic Stenger’s discussion list, even as long as few years ago. But if there is no measurement process in De Sitter space doesn’t this rule out any kind of vacua decay in inflation as well as the Carroll Chen proposal on the origin of universes? In fact wouldn’t it would rule out every possible model of the Universe’s origin . i.e. . Vilenkin, Linde, Hartle and Hawking, Atkatz and Pagel etc. How do you get from the quantum universe of the Wheeler De Witt equation , a static, timeless state , to the universe we actually live in? With the boundary as everything ( no boundary) there is no De Coherence process. If in De Sitter space nothing ever really happens, so much more the void of third quantization.
Thanks for the clarification, Sean.
Your second paragraph makes me wonder: the state you describe there sounds awfully similar to the state of the de Sitter space you’re describing. If so, wouldn’t everything be entangled and in equilibrium? How, then, would such a space transition to the one we’re familiar with?
b&
Bob– Ordinary tunneling down from a false vacuum to a true one is perfectly allowed by our analysis, since it increases entropy and generates decoherence.
Ben– If we are in a perfect de Sitter vacuum, we’re saying there will be no transitions to anything. But we’re probably not; it’s easy to imagine a landscape of many different approximate vacua.
From my studies of pop physics, I was under the impression that “quantum fluctuation” was synonymous with random particle pair creation and annihilation (that would be a mouth full). So then there very well could be “quantum fluctuations”, because the mechanism behind random particle pair creation and annihilation are unknown. Then I thought that was the reason why Michio Kaku ask the question of why there is not enough antimatter in the universe, because if the “quantum fluctuations” are random particle pair creation and annihilation then the universe would have to be half antimatter. But then, from the “cosmology experiment” the universe is mostly matter, so then the “cosmology experiment” shows that was not the case, unless there was some unknown reason why the universe isn’t half antimatter.
Ah — I think I get it; it’s an approximation useful for certain scales. Just as it’s useful to approximate the Earth as flat when you’re spreading that street map out on the table.
So, the Cosmos (perhaps, if you’re right) approximates a perfect de Sitter vacuum, and, in that context (which is at the same scale) Boltzmann Brains and the like aren’t relevant. But at different scales (where Boltzmann Brains aren’t relevant) it deviates enough from a perfect de Sitter vacuum for local dechoerence and all the rest — just as the Earth clearly isn’t actually flat if you’re floating by the window of the ISS.
Thanks!
b&
Sounds like a great paper, though I don’t think I quite understand it.
So, during inflation, the inflaton field is at a higher potential, rolling down to a lower potential. That means it’s not in the lowest energy state, and not a vacuum state–maybe it’s a false vacuum state? Is that right?
Another question, how does entropy figure into this? Fluctuations in the CMBR seem to represent huge amount of free energy. Where did that free energy come from? Why can’t that free energy go into creating Boltzmann brains?
I slogged through the paper, I will need to read it several times to get some decent degree of understanding. However, for what’s it worth, I think the basic premise, that you can’t have quantum fluctuations absent a measurement process ( De Coherence) is without doubt right. The rub will be whether or not a De Sitter space is really free of any measurement process. I hope this paper stimulates some responses from folk like Linde who are bound to approch these assertions very critically. This is a very interesting paper.
Hi Professor Carroll,
What is the best explanation to quantum fluctuations? I mean why do Q. fluctuantions occur? Do We really do not have the ”cause” of it? Is it just a consequence of Heisenberg´s principle? (that is not the ”cause”?) I know the word “cause” is problematic.
And about TIME, Do quantum fluctuations occur without time? I mean out of time. Not needing the influence of time. Without the existence of time.
Could it be one reason to suspect the time is fundamental?
Thank You.
If the universe/multiverse is infinite, do you still get an infinite number of Boltzmann brains, as long as their probability is finite in an infinite number of finite patches? If so, is there a good way to calculate the ratio of Boltzmann brains to normal observers? Or are you thinking that it’s just Bang – us – de Sitter, end of story?
Doesn’t a Boltzmann Brain count as an observer? Or for that matter, a Boltzmann Bowl of Petunias (since intelligence isn’t really needed to be an observer)?
Edit: oops! on rereading, I see the sentence ‘The idea that Boltzmann brains fluctuate into existence and should count as “observers”…has been a troubling one,’ which makes my question above seem lifted from the text. But my question isn’t about my worry that only empty space exists outside my office door. It’s about the concept: “there are no particle detectors around”. Don’t the Boltzmann Brains and Boltzmann Bowls of Petunias themselves count as particle detectors?
miller– The kind of inflation that we think gave rise to density perturbations is “slow-roll” inflation, where a field is slowly rolling down its potential. So it’s not really in a vacuum state at all. Nevertheless, it can be very close to the vacuum state; in particular, not entangled with anything else.
Alexandre– Quantum fluctuations occur because the universe is fundamentally quantum-mechanical, and observations typically probe quantities (like position or momentum) that are not precisely defined in a quantum state.
Eric– We’re saying that the probability of fluctuating a Boltzmann brain goes to zero, so the integral over all time is finite (and likely quite small).
Charlie– The informal notion of an “observer” requires a macroscopic system that is out of equilibrium. In de Sitter space, everything is in equilibrium.
Hello Professor,
I wonder how these new ideas of yours relate to your previous work on the arrow of time. The impression I get from this ( I’m just a layman,I’m no physicist, so I am most likely off) is that once the Universe expands enough to become the true De Sitter space, the universe is effectively dead. No more work can happen, and it is basically in a state of true heat death.
In your previous work, you seem to indicate (again, I may be misinterpreting here) that there may not be a true final “end” to work in the universe, and that it can still achieve a low entropy state given enough time, random chance etc. Are you saying that the work that you have down and your thoughts that you wrote about in “From Eternity To Here” are now no longer valid according to you? If so, how do you now resolve the questions of how the universe started in a low entropy state, and how do you reconcile the ideas of time reversible laws of physics into your new view?
This makes a lot of sense, and is now my default view of things. Good work! I’ll worry less about Boltzman brains and worry more about where inflation comes from, since it probably isn’t eternal.
Michael– Your impression is correct, but only if de Sitter space is truly an equilibrium vacuum state. If it is unstable (for example, to nucleating baby universes, or to decaying to a lower-energy vacuum), then interesting things can still happen, including the scenario I discussed in FETH.
Let me ask the dumb question. If you have the Inflaton field slow rolling down the potential hill, how can we say we have a static unmeasured quantum state. Isn’t the value of the Inflaton field potential the result of a measurement process? This being the case how does this process evade “experiencing” quantum fluctuations.
Dr. Carroll,
In your paper “DeSitter Space Without Quantum Fluctuations,” you and your co-authors state in Section 6, under “Conclusions”:
“In stationary states, entropy is not generated, and the wave function remains fixed; therefore, there are no quantum fluctuations….” (p.28).
The “nothing theorists,” including Dr. Stephen Hawking, Dr. Lawrence M. Krauss, and Dr. Alex Vilenkin all propose a Cosmic Origin scenario with reference to a “quantum fluctuation”:
1.) “Absolute nothingness” phase transitions via 2.) a “quantum fluctuation” to 3.) Our Cosmos.
“Absolute nothingness” is variously defined as a.) “a closed spherical spacetime of zero radius.” (Dr. Vilenkin); b.) “… no space, no time, no anything!” (Dr. Krauss); and c.) “…some peculiar non-geometric phase where we wouldn’t recognize it as ‘space’ at all.” (Dr. Sean M. Carroll).
Using the above quote from your paper of 1 May 2014, can we now look at this “Nothingness Origin” scenario in the following way:
(1.) “Absolute nothingness” is unquestionably a “stationary state.”
(2.) “Entropy” is not generated; as a physicalist you must know that this “nothingness,” as defined, is a metaphysical construct: the “W” in L. Boltzmann’s formula for entropy (S=k log W) is, in “absolute nothingness,” ZERO, A NULL SET.
(3.) The “wave function” remains fixed in this “nothingness state”—if we can talk at all in these quantum mechanical terms with reference to “absolute nothingness.” Therefore:
(4.) “THERE ARE NO QUANTUM FLUCTUATIONS.”
If there are no “quantum fluctuations” in this Origin scenario, a key transitional element is now lost in the “nothing” program of “A Universe From Nothing!”
In your book “From Eternity to Here,” in note 232 on page 405, you reference the Gottfried Wilhelm Leibniz existential question “Why is there something rather than nothing;” and you declare the classical ontological definition of nothing as a genesis “state,” “neither…warranted by either experience or logic.” My question to you Dr. Carroll is twofold:
(A.) Are not the above quoted definitions of “absolute nothing” really EQUIVALENT to the classical ontological definition of nothing? and
(B.) In the conceptual perspective of your post “DeSitter Space Without Quantum Fluctuations” paper, do you find, now, the above described Origins scenario from “absolute nothing” as “neither…warranted by either experience or logic?”
T.E. Oakley
Sent from my iPhone
How does this sit for virtual particles and the Casimir effect?
Err, please excuse the completely non-scientist question, but I’d like Sean to explain this in simple terms…
In the comments you seem to say that the macroscopic system has a kind of “imprint” that defines “where it comes from”. Like in science fiction usually is defined as a “vibration”, with parallel words having different vibrations or phases. So it seems you say that when an observation occurs, the entanglement happens because it’s the fingerprint of the macroscopic system that gives a peculiarity to the thing observed.
In other words, the thing observed wasn’t originally moving, but it is moved through the act of observation and fixed in a position. Or, it’s the interaction between the thing and what was observing that produces the result.
But if this isn’t a totally incorrect simplification, why are even we aware of this quantum theory if as an observing system we are always tied to “our way of seeing”? What’s the theoretical external observer that tells us there is more than one possible state?
Does the de Sitter space for this paper include the Goldstone Theorem?
One thing I found peculiar about inflation is that it assumes that there wasn’t that much matter/energy close to the Big Bang, but the inflation field consisted of something that was unable to change density. Then what was able to expand with the universe but not change in density was a mystery, but that was how Alan Guth was able to discover inflation. Then I thought if there was a free energy mechanism involved that resulted in the Big Bang, then the creation of energy could then act like a field that didn’t change in density. It could just create more particles as it grew, so that the total density would remain unchanging even though it had grew in size. It would be kind of funny if that was one of the skeletons hiding in inflation’s closet.
John Barret writes:
“One thing I found peculiar about inflation is that it assumes that there wasn’t that much matter/energy close to the Big Bang, but the inflation field consisted of something that was unable to change density. Then what was able to expand with the universe but not change in density was a mystery, but that was how Alan Guth was able to discover inflation. Then I thought if there was a free energy mechanism involved that resulted in the Big Bang, then the creation of energy could then act like a field that didn’t change in density. It could just create more particles as it grew, so that the total density would remain unchanging even though it had grew in size. It would be kind of funny if that was one of the skeletons hiding in inflation’s closet.”
Two words, Dark Energy.
Abalieno writes
“(A.) Are not the above quoted definitions of “absolute nothing” really EQUIVALENT to the classical ontological definition of nothing? and
(B.) In the conceptual perspective of your post “DeSitter Space Without Quantum Fluctuations” paper, do you find, now, the above described Origins scenario from “absolute nothing” as “neither…warranted by either experience or logic?”
If we truly live in a quantum universe where the classical reality we observe is the product of wave function reduction, then there exists a quantum state of everything that is not time dependent. What we observe is highly coarse grained view of this, so time dependence is emergent.
Interesting stuff, Sean. I’m not keen on talk of Boltzmann brains and the multiverse myself, but nevermind. IMHO yes, there were no quantum fluctuations. Because the energy density was so high the whole universe was subject to something similar to gravitational time dilation. Like a black hole event horizon is. And because the time dilation is infinite, it takes forever for a fluctuation to occur. So it never ever does. Which means Hawking radiation doesn’t occur either.