One of the most profound and mysterious principles in all of physics is the Born Rule, named after Max Born. In quantum mechanics, particles don’t have classical properties like “position” or “momentum”; rather, there is a wave function that assigns a (complex) number, called the “amplitude,” to each possible measurement outcome. The Born Rule is then very simple: it says that the probability of obtaining any possible measurement outcome is equal to the square of the corresponding amplitude. (The wave function is just the set of all the amplitudes.)
Born Rule: ![]()
The Born Rule is certainly correct, as far as all of our experimental efforts have been able to discern. But why? Born himself kind of stumbled onto his Rule. Here is an excerpt from his 1926 paper:
That’s right. Born’s paper was rejected at first, and when it was later accepted by another journal, he didn’t even get the Born Rule right. At first he said the probability was equal to the amplitude, and only in an added footnote did he correct it to being the amplitude squared. And a good thing, too, since amplitudes can be negative or even imaginary!
The status of the Born Rule depends greatly on one’s preferred formulation of quantum mechanics. When we teach quantum mechanics to undergraduate physics majors, we generally give them a list of postulates that goes something like this:
- Quantum states are represented by wave functions, which are vectors in a mathematical space called Hilbert space.
- Wave functions evolve in time according to the Schrödinger equation.
- The act of measuring a quantum system returns a number, known as the eigenvalue of the quantity being measured.
- The probability of getting any particular eigenvalue is equal to the square of the amplitude for that eigenvalue.
- After the measurement is performed, the wave function “collapses” to a new state in which the wave function is localized precisely on the observed eigenvalue (as opposed to being in a superposition of many different possibilities).
It’s an ungainly mess, we all agree. You see that the Born Rule is simply postulated right there, as #4. Perhaps we can do better.
Of course we can do better, since “textbook quantum mechanics” is an embarrassment. There are other formulations, and you know that my own favorite is Everettian (“Many-Worlds”) quantum mechanics. (I’m sorry I was too busy to contribute to the active comment thread on that post. On the other hand, a vanishingly small percentage of the 200+ comments actually addressed the point of the article, which was that the potential for many worlds is automatically there in the wave function no matter what formulation you favor. Everett simply takes them seriously, while alternatives need to go to extra efforts to erase them. As Ted Bunn argues, Everett is just “quantum mechanics,” while collapse formulations should be called “disappearing-worlds interpretations.”)
Like the textbook formulation, Everettian quantum mechanics also comes with a list of postulates. Here it is:
- Quantum states are represented by wave functions, which are vectors in a mathematical space called Hilbert space.
- Wave functions evolve in time according to the Schrödinger equation.
That’s it! Quite a bit simpler — and the two postulates are exactly the same as the first two of the textbook approach. Everett, in other words, is claiming that all the weird stuff about “measurement” and “wave function collapse” in the conventional way of thinking about quantum mechanics isn’t something we need to add on; it comes out automatically from the formalism.
The trickiest thing to extract from the formalism is the Born Rule. That’s what Charles (“Chip”) Sebens and I tackled in our recent paper:
Self-Locating Uncertainty and the Origin of Probability in Everettian Quantum Mechanics
Charles T. Sebens, Sean M. CarrollA longstanding issue in attempts to understand the Everett (Many-Worlds) approach to quantum mechanics is the origin of the Born rule: why is the probability given by the square of the amplitude? Following Vaidman, we note that observers are in a position of self-locating uncertainty during the period between the branches of the wave function splitting via decoherence and the observer registering the outcome of the measurement. In this period it is tempting to regard each branch as equiprobable, but we give new reasons why that would be inadvisable. Applying lessons from this analysis, we demonstrate (using arguments similar to those in Zurek’s envariance-based derivation) that the Born rule is the uniquely rational way of apportioning credence in Everettian quantum mechanics. In particular, we rely on a single key principle: changes purely to the environment do not affect the probabilities one ought to assign to measurement outcomes in a local subsystem. We arrive at a method for assigning probabilities in cases that involve both classical and quantum self-locating uncertainty. This method provides unique answers to quantum Sleeping Beauty problems, as well as a well-defined procedure for calculating probabilities in quantum cosmological multiverses with multiple similar observers.
Chip is a graduate student in the philosophy department at Michigan, which is great because this work lies squarely at the boundary of physics and philosophy. (I guess it is possible.) The paper itself leans more toward the philosophical side of things; if you are a physicist who just wants the equations, we have a shorter conference proceeding.
Before explaining what we did, let me first say a bit about why there’s a puzzle at all. Let’s think about the wave function for a spin, a spin-measuring apparatus, and an environment (the rest of the world). It might initially take the form
(α[up] + β[down] ; apparatus says “ready” ; environment0). (1)
This might look a little cryptic if you’re not used to it, but it’s not too hard to grasp the gist. The first slot refers to the spin. It is in a superposition of “up” and “down.” The Greek letters α and β are the amplitudes that specify the wave function for those two possibilities. The second slot refers to the apparatus just sitting there in its ready state, and the third slot likewise refers to the environment. By the Born Rule, when we make a measurement the probability of seeing spin-up is |α|2, while the probability for seeing spin-down is |β|2.
In Everettian quantum mechanics (EQM), wave functions never collapse. The one we’ve written will smoothly evolve into something that looks like this:
α([up] ; apparatus says “up” ; environment1)
+ β([down] ; apparatus says “down” ; environment2). (2)
This is an extremely simplified situation, of course, but it is meant to convey the basic appearance of two separate “worlds.” The wave function has split into branches that don’t ever talk to each other, because the two environment states are different and will stay that way. A state like this simply arises from normal Schrödinger evolution from the state we started with.
So here is the problem. After the splitting from (1) to (2), the wave function coefficients α and β just kind of go along for the ride. If you find yourself in the branch where the spin is up, your coefficient is α, but so what? How do you know what kind of coefficient is sitting outside the branch you are living on? All you know is that there was one branch and now there are two. If anything, shouldn’t we declare them to be equally likely (so-called “branch-counting”)? For that matter, in what sense are there probabilities at all? There was nothing stochastic or random about any of this process, the entire evolution was perfectly deterministic. It’s not right to say “Before the measurement, I didn’t know which branch I was going to end up on.” You know precisely that one copy of your future self will appear on each branch. Why in the world should we be talking about probabilities?
Note that the pressing question is not so much “Why is the probability given by the wave function squared, rather than the absolute value of the wave function, or the wave function to the fourth, or whatever?” as it is “Why is there a particular probability rule at all, since the theory is deterministic?” Indeed, once you accept that there should be some specific probability rule, it’s practically guaranteed to be the Born Rule. There is a result called Gleason’s Theorem, which says roughly that the Born Rule is the only consistent probability rule you can conceivably have that depends on the wave function alone. So the real question is not “Why squared?”, it’s “Whence probability?”
Of course, there are promising answers. Perhaps the most well-known is the approach developed by Deutsch and Wallace based on decision theory. There, the approach to probability is essentially operational: given the setup of Everettian quantum mechanics, how should a rational person behave, in terms of making bets and predicting experimental outcomes, etc.? They show that there is one unique answer, which is given by the Born Rule. In other words, the question “Whence probability?” is sidestepped by arguing that reasonable people in an Everettian universe will act as if there are probabilities that obey the Born Rule. Which may be good enough.
But it might not convince everyone, so there are alternatives. One of my favorites is Wojciech Zurek’s approach based on “envariance.” Rather than using words like “decision theory” and “rationality” that make physicists nervous, Zurek claims that the underlying symmetries of quantum mechanics pick out the Born Rule uniquely. It’s very pretty, and I encourage anyone who knows a little QM to have a look at Zurek’s paper. But it is subject to the criticism that it doesn’t really teach us anything that we didn’t already know from Gleason’s theorem. That is, Zurek gives us more reason to think that the Born Rule is uniquely preferred by quantum mechanics, but it doesn’t really help with the deeper question of why we should think of EQM as a theory of probabilities at all.
Here is where Chip and I try to contribute something. We use the idea of “self-locating uncertainty,” which has been much discussed in the philosophical literature, and has been applied to quantum mechanics by Lev Vaidman. Self-locating uncertainty occurs when you know that there multiple observers in the universe who find themselves in exactly the same conditions that you are in right now — but you don’t know which one of these observers you are. That can happen in “big universe” cosmology, where it leads to the measure problem. But it automatically happens in EQM, whether you like it or not.
Think of observing the spin of a particle, as in our example above. The steps are:
- Everything is in its starting state, before the measurement.
- The apparatus interacts with the system to be observed and becomes entangled. (“Pre-measurement.”)
- The apparatus becomes entangled with the environment, branching the wave function. (“Decoherence.”)
- The observer reads off the result of the measurement from the apparatus.
The point is that in between steps 3. and 4., the wave function of the universe has branched into two, but the observer doesn’t yet know which branch they are on. There are two copies of the observer that are in identical states, even though they’re part of different “worlds.” That’s the moment of self-locating uncertainty. Here it is in equations, although I don’t think it’s much help.
You might say “What if I am the apparatus myself?” That is, what if I observe the outcome directly, without any intermediating macroscopic equipment? Nice try, but no dice. That’s because decoherence happens incredibly quickly. Even if you take the extreme case where you look at the spin directly with your eyeball, the time it takes the state of your eye to decohere is about 10-21 seconds, whereas the timescales associated with the signal reaching your brain are measured in tens of milliseconds. Self-locating uncertainty is inevitable in Everettian quantum mechanics. In that sense, probability is inevitable, even though the theory is deterministic — in the phase of uncertainty, we need to assign probabilities to finding ourselves on different branches.
So what do we do about it? As I mentioned, there’s been a lot of work on how to deal with self-locating uncertainty, i.e. how to apportion credences (degrees of belief) to different possible locations for yourself in a big universe. One influential paper is by Adam Elga, and comes with the charming title of “Defeating Dr. Evil With Self-Locating Belief.” (Philosophers have more fun with their titles than physicists do.) Elga argues for a principle of Indifference: if there are truly multiple copies of you in the world, you should assume equal likelihood for being any one of them. Crucially, Elga doesn’t simply assert Indifference; he actually derives it, under a simple set of assumptions that would seem to be the kind of minimal principles of reasoning any rational person should be ready to use.
But there is a problem! Naïvely, applying Indifference to quantum mechanics just leads to branch-counting — if you assign equal probability to every possible appearance of equivalent observers, and there are two branches, each branch should get equal probability. But that’s a disaster; it says we should simply ignore the amplitudes entirely, rather than using the Born Rule. This bit of tension has led to some worry among philosophers who worry about such things.
Resolving this tension is perhaps the most useful thing Chip and I do in our paper. Rather than naïvely applying Indifference to quantum mechanics, we go back to the “simple assumptions” and try to derive it from scratch. We were able to pinpoint one hidden assumption that seems quite innocent, but actually does all the heavy lifting when it comes to quantum mechanics. We call it the “Epistemic Separability Principle,” or ESP for short. Here is the informal version (see paper for pedantic careful formulations):
ESP: The credence one should assign to being any one of several observers having identical experiences is independent of features of the environment that aren’t affecting the observers.
That is, the probabilities you assign to things happening in your lab, whatever they may be, should be exactly the same if we tweak the universe just a bit by moving around some rocks on a planet orbiting a star in the Andromeda galaxy. ESP simply asserts that our knowledge is separable: how we talk about what happens here is independent of what is happening far away. (Our system here can still be entangled with some system far away; under unitary evolution, changing that far-away system doesn’t change the entanglement.)
The ESP is quite a mild assumption, and to me it seems like a necessary part of being able to think of the universe as consisting of separate pieces. If you can’t assign credences locally without knowing about the state of the whole universe, there’s no real sense in which the rest of the world is really separate from you. It is certainly implicitly used by Elga (he assumes that credences are unchanged by some hidden person tossing a coin).
With this assumption in hand, we are able to demonstrate that Indifference does not apply to branching quantum worlds in a straightforward way. Indeed, we show that you should assign equal credences to two different branches if and only if the amplitudes for each branch are precisely equal! That’s because the proof of Indifference relies on shifting around different parts of the state of the universe and demanding that the answers to local questions not be altered; it turns out that this only works in quantum mechanics if the amplitudes are equal, which is certainly consistent with the Born Rule.
See the papers for the actual argument — it’s straightforward but a little tedious. The basic idea is that you set up a situation in which more than one quantum object is measured at the same time, and you ask what happens when you consider different objects to be “the system you will look at” versus “part of the environment.” If you want there to be a consistent way of assigning credences in all cases, you are led inevitably to equal probabilities when (and only when) the amplitudes are equal.
What if the amplitudes for the two branches are not equal? Here we can borrow some math from Zurek. (Indeed, our argument can be thought of as a love child of Vaidman and Zurek, with Elga as midwife.) In his envariance paper, Zurek shows how to start with a case of unequal amplitudes and reduce it to the case of many more branches with equal amplitudes. The number of these pseudo-branches you need is proportional to — wait for it — the square of the amplitude. Thus, you get out the full Born Rule, simply by demanding that we assign credences in situations of self-locating uncertainty in a way that is consistent with ESP.
We like this derivation in part because it treats probabilities as epistemic (statements about our knowledge of the world), not merely operational. Quantum probabilities are really credences — statements about the best degree of belief we can assign in conditions of uncertainty — rather than statements about truly stochastic dynamics or frequencies in the limit of an infinite number of outcomes. But these degrees of belief aren’t completely subjective in the conventional sense, either; there is a uniquely rational choice for how to assign them.
Working on this project has increased my own personal credence in the correctness of the Everett approach to quantum mechanics from “pretty high” to “extremely high indeed.” There are still puzzles to be worked out, no doubt, especially around the issues of exactly how and when branching happens, and how branching structures are best defined. (I’m off to a workshop next month to think about precisely these questions.) But these seem like relatively tractable technical challenges to me, rather than looming deal-breakers. EQM is an incredibly simple theory that (I can now argue in good faith) makes sense and fits the data. Now it’s just a matter of convincing the rest of the world!

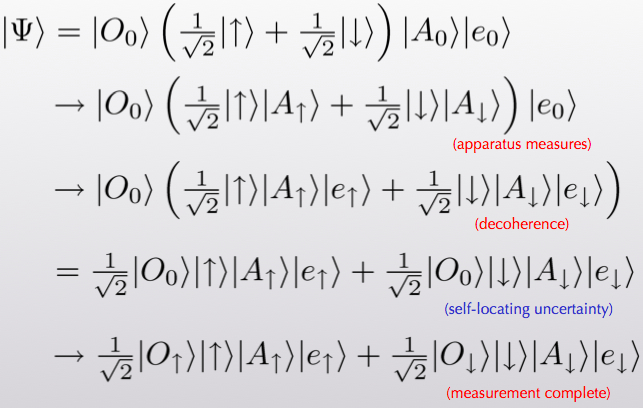
One problem I have with all of these attempts to get the born rule (the problem applies equally to your approach and to the Deutsch-Wallace approach) is that they all go like this.
1. Assume decoherence gets you branches in some preferred basis.
2. Give an argument that the Born rule applied to the amplitudes of these branches yields something worthy of the name ‘probability.’
The problem is that these steps happen in the reverse order that one would like them to happen. Look at step one. Decoherence arguments involve steps
1.a) showing that as the system+detector gets entangled with the environment, the reduced density matrix of this entangled pair evolves such that all the off-diagonal elements get very close to zero,
and
1.b)reasoning that therefore, each diagonal element corresponds to an emergent causally inert “branch.”
But step 1.b is fishy insofar as it happens before step 2. Who cares if the little numbers on the off-diagonals are very close to zero, until I know what their physical interpretation is? Not all very small numbers in physics can be interpreted as standing in front of unimportant things. Now, if we could accomplish step 2, then we could discard the off-diagonal elements, because we know that very small _probabilities_ are unimportant. But the cart has been put in front of the horse. We can’t conclude that the “Branches” are real and causally inert and have independent “obsevers” in them _until_ we have a physical interpretation of the off-diagonal elements being small. But all of these Everettian moves do 1.b first, and only afterwards do 2.
“With this assumption in hand, we are able to demonstrate that Indifference does not apply to branching quantum worlds in a straightforward way”
– This is where I lose the thread of the argument. This is the key problem with MWI and I would appreciate an intuitive explanation. It’s like you’ve just proved that 2+2=5 but the key step is “straightforward but technical”
Eric, I’m not sure I follow the worry. The fact that the off-diagonal elements are small tells us that the different branches don’t interfere with each other in terms of their future evolution. I.e., I could evolve a branch forward in time, and the result is completely independent of the existence of the other branches. That doesn’t seem to rely directly on any probability interpretation, but maybe I’m missing something.
Rationalist– Have a look at the paper. Sometimes arguments just have to be technical. 🙂
Sean,
Even if the off-diagonal elements are small, they are nonzero, so technically the branches still interfere, correct? How does this happen, and how can this be measured?
The argument you give here shows how, given a particular wave function, the Born Rule gives the right credences for observing various outcomes. But how do you know the wave function in the first place?
In the real world, we know wave functions by observing relative frequencies of outcomes. For example, if you tell me that the device in your lab produces electrons with the (spin) wave function 1/sqrt(2) |up> + 1/sqrt(2) |down>, and I ask you how you know that, you’re not going to show me a mathematical derivation of what credence you should assign to up vs. down; you’re going to show me data from the test runs you made of the device, that recorded equal numbers of up electrons and down electrons.
But it seems to me that, if the MWI is true, we can’t draw that conclusion from the test data, because if the MWI is true, *any* wave function with nonzero amplitude for both |up> and |down> will produce a “world” in which equal numbers of up and down electrons are observed. So I don’t see how your argument justifies assigning equal amplitudes to |up> and |down> based on such test data.
Stewart– In principle, yes. But the numbers are incredibly super-tiny — you’d be better off looking at a glass of cool water and waiting for it to spontaneously evolve into an ice cube in a glass of warm water.
Peter– That’s something else we discuss in the paper. We show that the ordinary rules for Bayesian inference and hypothesis-testing are perfectly well respected by EQM. Of course unlikely things will happen, but that’s not what one should expect. It’s a big multiverse, so someone is going to be unlucky and experience very low-probability series of events (just as they would in a big classical universe).
Sean,
In principles, yes, so isn’t there anything sort of wrong about that? Anything that can happen, in quantum mechanics, will happen. So since the off-diagonals are nonzero, how will this interference take place when it happens? Can this be measured?
I admit I looked at the paper just so I could see your solution to the quantum sleeping beauty problem. Looks great! Makes me feel like some philosophical dilemmas really do have answers.
Hi Sean,
OK, maybe that helps. But let me be clear about what you are saying. Suppose for simplicity that my system plus detector evolves into only two “branches”. You say “I could evolve a branch forward in time, and the result is completely independent of the existence of the other branches” I take it you really mean, as you say in response to Steward, that the degree to which they are not completely independent is represented by numbers that are incredibly super tiny. But I still have no physical interpretation of those tiny effects. you say “you’d be better off looking at a glass of cool water and waiting for it to spontaneously evolve into an ice cube in a glass of warm water” but I don’t know how you can say what impact those small numbers have on what I am likely to see until you have interpreted them as relating to probabilities.
Sean,
The problem with the Everettian interpretation is that it assumes that QM is fundamentally correct. I think this is a fairly unsafe assumption and we have lots of (indirect) evidence to tell us that QM is incomplete.
Sure, if QM is complete as we know it, MWI is the simplest explanation. But it seems much more likely that QM is in fact not complete, and therefore any conclusions derived by assuming it is complete are meaningless.
Sean,
Whether to do the QM experiment at this moment is entirely arbitrary human decision. Is the branching taking place in observer’s mind or is it real? In either case this sounds like too much metaphysical. If the branching was decided before and the observer is just picking up a branch at random, that is even worse. In fact I am astonished that you can get away with such arguments when you openly attack religious and metaphysical arguments! Well, life is unfair!! Isn’t it?
Sean, you say that “Quantum probabilities are really credences … rather than statements about truly stochastic dynamics or frequencies in the limit of an infinite number of outcomes.” I don’t totally understand what you’re saying here — in the MWI, aren’t the probabilities both credences and frequencies? If I do a long sequence of approximately identical experiments, the quantum probabilities tell me the frequencies with which the different outcomes will be present in my branch of the wavefunction.
What about quantum recombination? Surely any physicality of all those copies is impossible if you intend to reconstitute a superposition in the same apparatus? Now you have a super super position of being in many worlds and not being in many worlds at the same time.
Sean,
Several remarks.
The first is that classical physics does indeed allow us to describe multiple worlds provided that we interpret classical probabilities according to something like David Lewis’s modal realism. When studying the evolution of classical probability distributions, all the states “are just there” in the formalism, so why not simply accept that they exist in reality, as one does in EQM?
My second remark is about axioms. All logical claims consist of premises (axioms), arguments that follow from those premises, and conclusions, and EQM is no different. Proponents often suggest that EQM doesn’t need as many axioms as the traditional interpretations. But the trouble with EQM is that although it seems at first like you don’t need very many axioms, the truth is that you do. Simply insisting that we don’t mess with the superposition rule isn’t enough. Quantum-information instrumentalism (say, QBism) doesn’t mess with superpositions either, and allows arbitrarily large systems to surperpose. Declaring that we must interpret the elements of a superpositions as physical parallel universes is therefore an affirmative, nontrivial axiom about the ontology of the theory, even if some people might regard it as an “obvious” axiom.
The pointer-variable argument also implicitly assumes axioms as well. We have to declare that something singles out a preferred basis (for the cat, this means that we need to single out the alive vs. dead basis, rather than, say, the alive+dead vs. alive-dead basis). You can keep adding additional systems and environments, but at some point you have to declare that once you’ve added enough, you can shout “stop!” and pick your preferred basis. And what is our criterion for picking that basis? That’s going to be another axiom! And if you pick locality or something like that for specifying your preferred-basis-selection postulate, you have to contend with the fact that locality may not be a fundamental feature of reality once we figure out quantum gravity, so if we do add locality as part of our axiom for picking the preferred basis, the EQM interpretation is now sensitive to features of quantum gravity that we don’t know yet.
Finally, are you assuming that there’s some big universal wave function that evolves unitarily? Given all we know about eternal inflation, is this a reliable assumption anymore? Even if you’re willing to accept it, it represents another axiom to add on.
The problem with EQM is that this process of adding axioms keeps going on (your “epistemic separability principle,” for example, is another axiom, and far from an obvious one!), and even then we still have to contend with the serious trouble of trying to make sense of the concept of probability starting from deterministic assumptions, a serious philosophical problem on par with the is-ought problem of Hume.
So, to summarize, you can’t justifiably start by saying “Hey, I only need two axioms!” and then inserting additional axioms (some implicitly) as you proceed. At the end of the day, you’ll have as many axioms as (or more than), say, instrumentalism, but then you still have the weirdness of deriving probability from non-probability.
kashyap vasavada: Shorter – “Squirrel!”
True, Quantum theory is incomplete.The complete form is called Quantum Gravity. In the complete theory a quantum of energy is associated with a wave packet of spacetime called a graviton.The MWI can be considered as the spliting of the spacetime wave packet.There 10^60 possible states for the spacetime wave packet each separated by an energy gap E=hH from which the cosmological constant =3(E/hc)^2. Here H is the Hubble constant,h Planck’s const. and c the speed of light.That is Quantum gravity should be able to inteprate quantum theory and General Relativity in one single framework.
OK, biologist here so take it easy on me.
I’m still having trouble with the cartoon representation of MWI where you have a film splitting into two films. Is this supposed to apply only in (simple) cases of binary events? I understand the value of focusing on simple examples (spin-up/down), but what is the cartoon representation for a continuous range of possibilities (electron position)? Does the film split into an infinity of films? (A film shmear?)
[Asked in previous post but too late for answer.] Am I allowed to think of MWI as many superpositions rather than many universes? When the cartoon-filmstrip splits, I imagine all mass/energy doubling. However, when I think of Schrödinger’s Cat, it never occurred to me that you had 10 lbs of cat (before box closed), then somehow 20 lbs of cat (during superposition), then 10 lbs again when I observe it. It’s always been called Schrödinger’s Cat (singular) rather than Schrödinger’s Cats (plural) even before collapse. So why now must we have many worlds rather than one world in superposition?
And I have to ask (even though the answer seems obvious): Are there more worlds today than there were yesterday?
“There are still puzzles to be worked out, no doubt, especially around the issues of exactly how and when branching happens, …” I thought that a major appeal of this approach is that nothing “happens”. We have continuous evolution rather than “collapses” or any other magic moments.
@Reader297:
Thank you. I am a complete and abject layperson whose skill is reading English, not grasping the mathematics of quantum mechanics. But grasping English alone can you get you a little ways with a message as clear and consistent and easily stated as the Everettian premise: The sophisticated mathematical construction called the wave function, which to date matches quantum observations perfectly, describes the physical superposition of macroworlds. Then I read something like this article — a series of ideas, formulations, qualifications, theories and axioms dedicated to untying knots that, golly, just weren’t there in the beginning when I was promised the breath of simplicity itself — and nothing is quite so plain as the fact that there is nothing at all obvious about the “Many Worlds” interpretation, and that, for all the “evidence” at hand, the physical reality, if any, represented by the wave function is as far from being glimpsed as it has ever been.
About to run away, so some selective responses–
Eric– I think there is a fair point here, and I’m not sure I’ve thought it through completely. My feeling would be that it’s correct to say (1) off-diagonal terms are small, so branches evolve almost-independently, therefore (2) we can assign probabilities to branches, and once we do that we can (3) ask about the probability of the off-diagonal terms growing large and witnessing interference between branches. At the very least it seems like a self-consistent story.
D– The probabilities are credences at each individual branching. Of course they can lead to frequencies if you do many individual trials of some kind of experiment.
Charlie– The detailed process of branching is a technical problem worthy of more study, no doubt. As you say, there aren’t really any problems with energy conservation, once you understand how it works in regular quantum mechanics. (If you like, the thing that is conserved is the energy times the amplitude squared.)
Sean, so you said:
“(1) off-diagonal terms are small, so branches evolve almost-independently, therefore (2) we can assign probabilities to branches, and once we do that we can (3) ask about the probability of the off-diagonal terms growing large and witnessing interference between branches.”
So, “almost-independently” isn’t the same as “actually independently”, but let’s leave that aside for now. If the off-diagonal terms do grow large, then that invalidates the “off-diagonal terms are small” assumption, therefore the branches are definitely not independent, therefore you cannot assign probabilities. There’s nothing circular/inconsistent about this?
OK…so I probably don’t understand this too well. Heck, I never even read your paper.
I agree completely that the MWI is the simplest form of QM, and like the “disappearing-worlds interpretations.”
The real question is not whether MWI is a better way of looking at QM. The real question is whether QM is correct. Every physical law found to date has either proved itself an approximation, or is waiting for its day. QM is exceedingly likely just another law waiting for its day to end.
So if you assume that QM is in someway wrong, will infinite dimensional Hilbert spaces and perfect linearity remain? Because without those things MWI is a non starter.
MWI is built upon the one part of QM that is weakest – the collapse.
Most of the alternative ‘explanations’ of QM have an obvious place where collapse occurs due to limited bandwidth (any non linearity). It will have to be experiment that proves QM wrong, as it is pretty firmly entrenched in the Physics Community.
FWIW, here are my comments, believe-it-or-not derived independently just last evening, though I acknowledge having been recently strongly influenced by your take on the Many Worlds Interpretation of quantum mechanics:
Coherence consists of all possible relations
emanating from every point in continually evolving spacetime.
Present moment decoherence
descries an organic universe
exploding from a localizing identity
ceaselessly redefining present experience.
Boundless such states are invariably emergent
within endlessly evolving relations.
Each and every relation within the organic multiverse
resonates with all others;
its influence exponentially attenuating with spacetime remoteness.
It’s useful to recognize the synchronicity of coherence
on scales ranging from quantum to cosmic.
All portrayals of experience
are exquisitely sensitive to
localizing identity.
The experience of the organism
is largely determined by
the point of view, or perspective,
of its identity.
Whatever may be perceived is rooted in organic remembrance,
reflecting naught but current decoherence—
entanglement evolving as natively cognizing environment
energizes present experience
as an ever more discrete subset of boundless probabilities.
I’d love to see a formulaic reduction of these ideas.
Tom
Sean,
“There are still puzzles to be worked out, no doubt, especially around the issues of exactly how and when branching happens, and how branching structures are best defined. […] But these seem like relatively tractable technical challenges to me, rather than looming deal-breakers.”
I would really like to see how the pointer basis problem can be considered a technical challenge, let alone a tractable one. At best, you’ll need an additional set of axioms in the theory, which should fix the choice of the basis. But the looming feeling is that the task of actually formulating these axioms is equivalent to resolving the measurement problem and the Schrodinger’s cat paradox. And that may prove to be much more difficult than a mere technical challenge — just remember that people like von Neumann tried, failed and gave up on that challenge — so it’s certainly not going to be easy.
Best, 🙂
Marko
Sean, you have a weird accent where are you from?