Hidden in my papers with Chip Sebens on Everettian quantum mechanics is a simple solution to a fun philosophical problem with potential implications for cosmology: the quantum version of the Sleeping Beauty Problem. It’s a classic example of self-locating uncertainty: knowing everything there is to know about the universe except where you are in it. (Skeptic’s Play beat me to the punch here, but here’s my own take.)
The setup for the traditional (non-quantum) problem is the following. Some experimental philosophers enlist the help of a subject, Sleeping Beauty. She will be put to sleep, and a coin is flipped. If it comes up heads, Beauty will be awoken on Monday and interviewed; then she will (voluntarily) have all her memories of being awakened wiped out, and be put to sleep again. Then she will be awakened again on Tuesday, and interviewed once again. If the coin came up tails, on the other hand, Beauty will only be awakened on Monday. Beauty herself is fully aware ahead of time of what the experimental protocol will be.
So in one possible world (heads) Beauty is awakened twice, in identical circumstances; in the other possible world (tails) she is only awakened once. Each time she is asked a question: “What is the probability you would assign that the coin came up tails?”
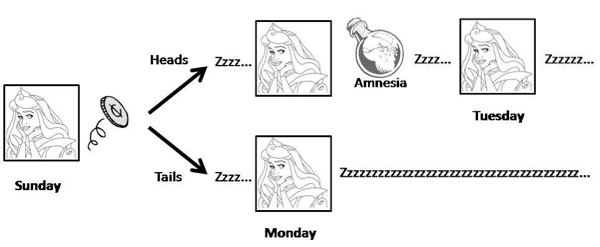
(Some other discussions switch the roles of heads and tails from my example.)
The Sleeping Beauty puzzle is still quite controversial. There are two answers one could imagine reasonably defending.
- “Halfer” — Before going to sleep, Beauty would have said that the probability of the coin coming up heads or tails would be one-half each. Beauty learns nothing upon waking up. She should assign a probability one-half to it having been tails.
- “Thirder” — If Beauty were told upon waking that the coin had come up heads, she would assign equal credence to it being Monday or Tuesday. But if she were told it was Monday, she would assign equal credence to the coin being heads or tails. The only consistent apportionment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.
The Sleeping Beauty puzzle has generated considerable interest. It’s exactly the kind of wacky thought experiment that philosophers just eat up. But it has also attracted attention from cosmologists of late, because of the measure problem in cosmology. In a multiverse, there are many classical spacetimes (analogous to the coin toss) and many observers in each spacetime (analogous to being awakened on multiple occasions). Really the SB puzzle is a test-bed for cases of “mixed” uncertainties from different sources.
Chip and I argue that if we adopt Everettian quantum mechanics (EQM) and our Epistemic Separability Principle (ESP), everything becomes crystal clear. A rare case where the quantum-mechanical version of a problem is actually easier than the classical version.
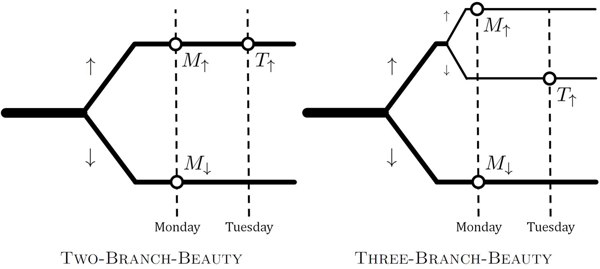
In the quantum version, we naturally replace the coin toss by the observation of a spin. If the spin is initially oriented along the x-axis, we have a 50/50 chance of observing it to be up or down along the z-axis. In EQM that’s because we split into two different branches of the wave function, with equal amplitudes.
Our derivation of the Born Rule is actually based on the idea of self-locating uncertainty, so adding a bit more to it is no problem at all. We show that, if you accept the ESP, you are immediately led to the “thirder” position, as originally advocated by Elga. Roughly speaking, in the quantum wave function Beauty is awakened three times, and all of them are on a completely equal footing, and should be assigned equal credences. The same logic that says that probabilities are proportional to the amplitudes squared also says you should be a thirder.
But! We can put a minor twist on the experiment. What if, instead of waking up Beauty twice when the spin is up, we instead observe another spin. If that second spin is also up, she is awakened on Monday, while if it is down, she is awakened on Tuesday. Again we ask what probability she would assign that the first spin was down.
This new version has three branches of the wave function instead of two, as illustrated in the figure. And now the three branches don’t have equal amplitudes; the bottom one is (1/√2), while the top two are each (1/√2)2 = 1/2. In this case the ESP simply recovers the Born Rule: the bottom branch has probability 1/2, while each of the top two have probability 1/4. And Beauty wakes up precisely once on each branch, so she should assign probability 1/2 to the initial spin being down. This gives some justification for the “halfer” position, at least in this slightly modified setup.
All very cute, but it does have direct implications for the measure problem in cosmology. Consider a multiverse with many branches of the cosmological wave function, and potentially many identical observers on each branch. Given that you are one of those observers, how do you assign probabilities to the different alternatives?
Simple. Each observer Oi appears on a branch with amplitude ψi, and every appearance gets assigned a Born-rule weight wi = |ψi|2. The ESP instructs us to assign a probability to each observer given by
![]()
It looks easy, but note that the formula is not trivial: the weights wi will not in general add up to one, since they might describe multiple observers on a single branch and perhaps even at different times. This analysis, we claim, defuses the “Born Rule crisis” pointed out by Don Page in the context of these cosmological spacetimes.
Sleeping Beauty, in other words, might turn out to be very useful in helping us understand the origin of the universe. Then again, plenty of people already think that the multiverse is just a fairy tale, so perhaps we shouldn’t be handing them ammunition.
Maybe you shouldn’t look at it as a division of the number of possible outcomes, but look at it as the odds of winning each event in succession. Sleeping Beauty would have a 1/2 chance of getting heads the first time. Then it would take getting another 1/2 in order for it to be Tuesday. That would mean that she would only get heads twice in a row 1/4 times. Then it would seem like she only had a 1/4 chance of it being Tuesday.
The number of possible outcomes may not be the total number of worlds, but it could be the total number of possible worlds that may or may not even occur.
If Beauty were told upon waking that the coin had come up heads, she would assign equal credence to it being Monday or Tuesday. But if she were told it was Monday, she would assign equal credence to the coin being heads or tails. The only consistent apportionment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.
How is it not consistent to assign 1/2 each to heads or tails, then split heads into 1/4 Monday and 1/4 Tuesday? I feel about this pretty much like about the earlier Born rule post; if you ignore the probabilities and just count distinct options, you’ll get the wrong answer.
Disclaimer: I read the Wikipedia page and still don’t understand the “thirder” position at all.
@JollyJoker
If Beauty assigns 1/4 probability to (heads & Monday), and 1/2 probability to (tails and Monday), and then if you told Beauty that it was Monday and not Tuesday, then she would be forced to assign 2/3 probability to tails. This is inconsistent.
@Sean
I’m not sure you can say I beat you to the punch, when it was right there in your paper!
Hi Sean,
As someone sympathetic to Many Worlds, I am trying hard to understand your paper as well as your last two blog posts, but to be honest, I find them opaque. I don’t have a specific question to bother you with, but I simply want to relay how how one member of your audience (me) has been reacting to your recent work (with confusion). The tone of your posts suggests this stuff is straightforward, but I suspect much of your audience is nonetheless confused (my friends and I have been, at least). I encourage you to keep refining and simplifying your message until it reaches a more convincing form. I still think the Born rule is a big problem for Many Worlds and I’m glad that you (and others) are tackling it. Good work so far, and good luck in the future.
I thought that your 1/3 sounded correct, but when I heard that certain other blogs were vigorously denouncing your answer I became certain that you must be correct.
Most questions of probability can be settled by the question, which side would you bet on? When SB is awakened she is given the opportunity to make a bet that the coin is heads: if it is heads, she is +$1. If it is tails, she is -$x. For what x is this a fair bet? There is a 50% probability of heads, in which case she is +$2 for her two wakings. There is a 50% probability of tails, in which case she is -$x. So x=2 for a fair bet, meaning that the probability is 1/3.
Presumably this argument is well-known. It is described on Wikipedia as the Phenomenalist position, which gives the result 1/3 unless the additional constraint is imposed that she can only bet on Monday, which is changing the problem: if we condition her probability on its being Monday, then of course it is 1/2.
So what’s the problem?
Joe, I think that’s a perfectly good argument. You can look at our argument as saying that an “epistemic” view of the problem gives an answer that is compatible with that more “operational” view (exactly as in the case of the Born Rule derivation). Having more than one way to get the right answer is a good thing, especially when people are skeptical of the right answer.
Before responding to the quantum version, I want to make sure I understand how you get the thirder position. The thirder position is based on the assumption that waking on each day has equal probability. However, this isn’t the case as waking up on Monday and Wednesday each have probability weights of 1 and Tuesday has a probability weight of 1/2. Each day itself has 1/3 probability from a perspective that isn’t Sleeping Beauty’s. So stated mathematically:
P(Wake|H and Mon) = P(Wake|T and Mon) = P(Wake|Mon) = 1
P(Wake|H and Wed) = P(Wake|T and Wed) = P(Wake|Wed) = 1
P(Wake|H and Tue) = 1
P(Wake|T and Tue) = 0
P(H) = P(T) = 1/2
P(Mon) = P(Tue) = P(Wed) = 1/3
So we want to find:
P(H|(Wake and Mon) or (Wake and Tue) or (Wake and Wed))
This is the statement, “What is the probability of the coin flip being heads given she wakes up on one and only one of the days, Monday, Tuesday, or Wednesday?”
P(H|(Wake and Mon) or (Wake and Tue) or (Wake and Wed)) =
P((Wake and Mon) or (Wake and Tue) or (Wake and Wed)|H)*P(H)/P((Wake and Mon) or (Wake and Tue) or (Wake and Wed)) by definition of conditional probability.
Let’s focus on calculating the denominator:
P((Wake and Mon) or (Wake and Tue) or (Wake and Wed)) =
P(Wake and Mon) + P(Wake and Tue) + P(Wake and Wed) =
P(Wake|Mon)*P(Mon) + P(Wake|Tue)*P(Tue) + P(Wake|Wed)*P(Wed)
1*1/3 + (1/2)*(1/3) + 1*1/3 = 5/6
The intersection cross terms are omitted because P(Mon and Wed) = 0, since they are mutually exclusive days.
Now let’s focus on the first term of the numerator:
P((Wake and Mon) or (Wake and Tue) or (Wake and Wed)|H) =
P(Wake and Mon|H) + P(Wake and Tue|H) + P(Wake and Wed|H) =
P(Wake|Mon and H)*P(Mon) + P(Wake|Tue and H)*P(Tue) + P(Wake|Wed and H)*P(Wed) = 1*1/3 + 1*1/3 + 1*1/3 = 1
So the whole expression is equal to:
P(H|(Wake and Mon) or (Wake and Tue) or (Wake and Wed)) = 1*(1/2)/(5/6) = 3/5
I don’t believe I made a mistake, but one of my probability assignments must be incorrect, meaning I misunderstand the statement of the problem.
3/5 makes a certain sense for heads though. While each day has equal chance (1/3), waking up on each day does not. You have 2 sets of cases, being woken up on Mon, Tue, and Wed; or being woken up just on Mon and Wed. Each day has 1/3 probability with each set of days having 1/2 probability, so 1/6 for waking up on each day. As a result, you have 5/6 cases Sleeping Beauty is awake and 1/6 cases of her not being awake. 3/6 cases are heads, the other 3/6 are tails, but she can only answer the question in 5 of those cases.
Regardless of the legitimacy of my attempted breakdown, I just don’t see how the odds of the coin being heads could ever drop below 1/2 if heads results in more wakeful days for sleeping beauty to sample versus tails.
This situation reminds me a little bit of the Monty Hall problem where upon first inspection you are also certain the probability must be 1/2 but it is not 1/2. Here is the wikipedia entry:
http://en.wikipedia.org/wiki/Monty_Hall_problem
Nevertheless this has nothing to do with QM really.
Everyone can make mistakes. Hopefully the other blog will admit it this time but I wouldn’t hold my breath.
Would someone mind explaining where expression 3.13 (in the arXiv paper) comes from?
To me, it looks like it assumes the Born rule to prove the Born rule. I’ll describe the situation:
Expression 3.11 tells us to assume a state that’s Sqrt(2/3)*UP + Sqrt(1/3)*DOWN.
Then expression 3.13 factors this expression into three terms, with a Sqrt(1/3) prefactor. It looks something like Sqrt(1/3)*(a*UP+b*UP+c*DOWN).
To me, it seems that this step is the magic that leads to the derivation ‘proving’ that UP is twice as common as DOWN. But as far as I can tell, this step is not justified in the text. Was it a mistake? Am I totally misreading something?
Thanks for any insight that you can offer.
Interesting……
There are four pieces of information, Monday, Tuesday, heads and tails and how they are presented matters to what Beauty can tell about the world. There are four possible scenarios:
1/
Beauty wakes up for the first time and is told it is Monday, so she knows that there is a 50% chance the coin has come up heads and 50% tails.
Beauty wakes up for the second time and is told it is Tuesday, so she knows that there is a 100% chance the coin has come up tails.
2/
Beauty wakes up for the first time and is told the coin has come up heads, so she knows that there is a 50% chance that it is Monday. If she is told the coin came up tails, the chance it is Monday is then 100%.
Beauty wakes up for the second time and is told the coin has come up heads, so she knows that there is a 50% chance that it is Tuesday.
3/
Beauty wakes up for the first time and is told the coin has come up heads, so she knows that there is a 50% chance that it is Monday. If she is told the coin came up tails, the chance it is Monday is then 100%.
Beauty wakes up for the second time and is told it is Tuesday, so she knows that there is a 100% chance the coin has come up heads.
4/
Beauty wakes up for the first time and is told it is Monday, so she knows that there is a 50% chance the coin has come up heads and 50% tails.
Beauty wakes up for the second time and is told the coin has come up heads, so she knows that there is a 50% chance that it is Tuesday.
In all these scenarios there are two pairs of variables Monday and Tuesday, and heads and tails, being given any one variable allows us to determine whether the two variables in the other pair have either a 50% or 100% probability.
What Elga seems to have done is to confuse the state of the coin given the day, with the day given the state of the coin when these two probabilities are entirely separate.
Ted– That equation just relies on Pythagoras’s theorem, which is true no matter what you believe about quantum mechanics. The Born Rule is a statement about the probabilities of measurement outcomes.
As mentioned in the previous post, the fact that the amplitude gets squared to give you probabilities is pretty trivial. What’s non-trivial is explaining why there are probabilities at all.
Ah, I caught my mistake in my analysis above, Sleeping Beauty is not interviewed Wednesday, this changes the probability of heads to 2/3, and tails to 1/3. I switched heads and tails following wikipedia’s description and not Sean’s, so this agrees with Sean’s answer. All is well. Sorry for spamming the comments with a lengthy calculation.
Joe, here’s the problem with that simple argument. (warning: I am a halfer).
Imagine the following situation: I flip a coin. I give you an opportunity to bet on whether it is heads or tails. And I ask you for what X is it a fair bet. But now I add the following wrinkle. If its comes up tails, I am going to make you bet twice. Now, I would say, your estimation of X no longer reflects your credence. I have messed with the rules too much. I think this is happening in the SB case.
(and that’s why the halfer argues that you should condition on it being monday, so that SB is prevented from betting twice on the same coin flip, if and only if it comes up tails. But maybe the wikipedia doesnt explain that well.)
Eric, the issue with that simplification is that the fact you are even being asked to bet at all is contingent on the outcome of the flip.
It is interesting that the famous mathematician Paul Erdos did not believe the solution of the Monty Hall problem until he was shown by a computer. This entry might elicit similar reactions. But that is mostly because once you’re “sure” you then proceed to become angry after you’re shown to be wrong. Then comes bargaining where you seek to alter the terms.
The coin is flipped only once. It could either be heads or tails, a 50-50 chance. When Sleeping Beauty is awoken either it would be Monday or Tuesday, no other choice, simply a 50-50 chance.
When she is awoken Beauty will not know whether she was awoken before or not, again simply a 50-50 chance.
When beauty is awoken what odds should she attribute to the probability that the coin toss was heads?
When awoken Beauty could be having her first interview or she also could have had one the day before. She would not know which, again just two choices. She should consider the odds as being 50-50 concerning whether the coin toss was heads or tails since (if) she gained no new information during the experiment.
The only consistent appointment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.
Problem is that the “probability” of a waking-up event has nothing to do with the “tails” probability: If SB always answers 1/3 for “tails” and you repeat the experiment e.g. 90 000 times, do you believe that “tails” will occur approximate 30 000 times?
(Remember we are told the coin is fair)
SB will get more correct interview-answers by saying “heads”, but she will still be correct in only about 50% of the experiments, i.e. coin-flips.
After first being with the halfers I slowly reasoned myself into the thirders position.
The halfers are only looking at the probability of the coin toss, disregarding the context in which the question was asked.
They answer the general question “what is the probability of tails when a coin is tossed?”
But the actual question is: “what is the probability of tails when the beauty wakes up?”.
I think the thirder argument is slightly off though.
Mixing up the information about if its monday or if heads came up seems wrong to me.
The only information that seems to make sense is how many possible waking up events there are in an outcome in relation to the sum of all waking up events in all outcomes. (So for tails 1 event / 3 total events)
There must be more to it though. This reasoning works only if heads and tails are equally likely.
If we have something else than a coin with say 1/3 chance of heads and 2/3 chance of tails it fails.
Guess I skip the quantum stuff – my head already exploded.
The trick is to realize there are 4 cases here, heads and Monday, tails and Monday, heads and Tuesday, tails and Tuesday. They each have 1/4 probability, but sleeping beauty only “samples” 3 of these cases, as she is not awake for tails and Tuesday. So of the 3 cases she sees, two of them are heads and if she wants to make money from betting, she’d better bet on heads.
Daniel your explanation is clear. I like it.
But it makes you wonder why people are publishing papers on this stuff, which is not uncertain and has nothing to do with QM.
So conditional probabilities can be tricky so what’s the relevance to QM?
Sean says “As mentioned in the previous post, the fact that the amplitude gets squared to give you probabilities is pretty trivial. What’s non-trivial is explaining why there are probabilities at all.”
erm, are you sure it’s trivial?
Why is this experiment considered worthwhile then?
You can notice that the probability function must be a positive definite form globally conservered by the unitary evolution (since probability is positive and globally equal to 1), but beyond that you are appealing to the consistency of the definition of probability for multiple outcomes – hence Gleason’s theorem. But that’s not a deduction, that’s us humans saying Nature wouldn’t be so stupid as to make the outcomes of measurements proportional to something other than the absolute square because it wouldn’t make sense compatible with us dumb humans understanding probability.
We can’t deduce the power 2, we can only marvel that the universe seems to obey that law.
Ignacio, I don’t know why it’s debated. If you correct my first post to not include Wednesday, it’s as explicit of a probability calculation you can get. The only way for it to be 1/2 is if Sleeping Beauty is awake for an equal number of coin flips. The solution to the Monty Hall problem also took a while to gain acceptance, though its paradox is a more subtle mistake in my opinion.
I think Sean is putting forth that the power of his branch probability assignments unequivocally have an answer to the problem. But I think probability does as well, as counting each state directly results in only one answer. It would be more interesting to apply ESP to uniquely conditional probability, quantum cases, like Born/Kochen-Specker type situations. An application to Bertrand’s paradox would actually be fascinating as a classical probability example.
Let me set up a different thought experiment. Again, the subject (me) knows the rules of the game. The rule is that my friend will knock me out, then role a pair of fair dice. If the dice come up snake eyes (both one’s), then he will put me in room A. Anything else and he will put me in room B. The two rooms are indistinguishable from the inside. So when I wake up, what odds should I take that I am in room A?
Does anyone here want to argue that I should consider it 50/50 that I am in room A? If not, can you explain why this answer would be different than the “thirder” position above?
Daniel it is not all that different. The bottom line is that you have to take the rules seriously. In the Monty Hall problem you need to understand that there is someone in the background who behaves predictably and has the answers. In this case the sampling is biased, I guess it is one way to characterize it.
But it has NOTHING to do with QM. It is just trickier than first meets the eye. That’s all.