Nothing focuses the mind like a hanging, and nothing focuses the science like an unexpected experimental result. The BICEP2 claimed discovery of gravitational waves in the cosmic microwave background — although we still don’t know whether it will hold up — has prompted cosmologists to think hard about the possibility that inflation happened at a very high energy scale. The BICEP2 paper has over 600 citations already, or more than 3/day since it was released. And hey, I’m a cosmologist! (At times.) So I am as susceptible to being prompted as anyone.
Cosmic inflation, a period of super-fast accelerated expansion in the early universe, was initially invented to help explain why the universe is so flat and smooth. (Whether this is a good motivation is another issue, one I hope to talk about soon.) In order to address these problems, the universe has to inflate by a sufficiently large amount. In particular, we have to have enough inflation so that the universe expands by a factor of more than 1022, which is about e50. Since physicists think in exponentials and logarithms, we usually just say “inflation needs to last for over 50 e-folds” for short.
So Grant Remmen, a grad student here at Caltech, and I have been considering a pretty obvious question to ask: if we assume that there was cosmic inflation, how much inflation do we actually expect to have occurred? In other words, given a certain inflationary model (some set of fields and potential energies), is it most likely that we get lots and lots of inflation, or would it be more likely to get just a little bit? Everyone who invents inflationary models is careful enough to check that their proposals allow for sufficient inflation, but that’s a bit different from asking whether it’s likely.
The result of our cogitations appeared on arxiv recently:
How Many e-Folds Should We Expect from High-Scale Inflation?
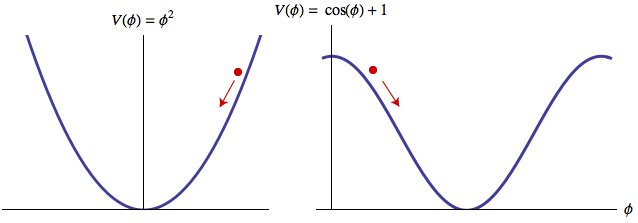
Grant N. Remmen, Sean M. CarrollWe address the issue of how many e-folds we would naturally expect if inflation occurred at an energy scale of order 1016 GeV. We use the canonical measure on trajectories in classical phase space, specialized to the case of flat universes with a single scalar field. While there is no exact analytic expression for the measure, we are able to derive conditions that determine its behavior. For a quadratic potential V(ϕ)=m2ϕ2/2 with m=2×1013 GeV and cutoff at MPl=2.4×1018 GeV, we find an expectation value of 2×1010 e-folds on the set of FRW trajectories. For cosine inflation V(ϕ)=Λ4[1−cos(ϕ/f)] with f=1.5×1019 GeV, we find that the expected total number of e-folds is 50, which would just satisfy the observed requirements of our own Universe; if f is larger, more than 50 e-folds are generically attained. We conclude that one should expect a large amount of inflation in large-field models and more limited inflation in small-field (hilltop) scenarios.
As should be evident, this builds on the previous paper Grant and I wrote about cosmological attractors. We have a technique for finding a measure on the space of cosmological histories, so it is natural to apply that measure to different versions of inflation. The result tells us — at least as far as the classical dynamics of inflation are concerned — how much inflation one would “naturally” expect in a given model.
The results were interesting. For definiteness we looked at two specific simple models: quadratic inflation, where the potential for the inflaton ϕ is simply a parabola, and cosine (or “natural“) inflation, where the potential is — wait for it — a cosine. There are many models one might consider (one recent paper looks at 193 possible versions of inflation), but we weren’t trying to be comprehensive, merely illustrative. And these are two nice examples of two different kinds of potentials: “large-field” models where the potential grows without bound (or at least until you reach the Planck scale), and “small-field” models where the inflaton can sit near the top of a hill.
Think for a moment about how much inflation can occur (rather than “probably does”) in these models. Remember that the inflaton field acts just like a ball rolling down a hill, except that there is an effective “friction” from the expansion of the universe. That friction becomes greater as the expansion rate is higher, which for inflation happens when the field is high on the potential. So in the quadratic case, even though the slope of the potential (and therefore the force pushing the field downwards) grows quite large when the field is high up, the friction is also very large, and it’s actually the increased friction that dominates in this case. So the field rolls slowly (and the universe inflates) at large values, while inflation stops at smaller values. But there is a cutoff, since we can’t let the potential grow larger than the Planck scale. So the quadratic model allows for a large but finite amount of inflation.
The cosine model, on the other hand, allows for a potentially infinite amount of inflation. That’s because the potential has a maximum at the top of the hill. In principle, there is a trajectory where the field simply sits there and inflates forever. Slightly more realistically, there are other trajectories that start (with zero velocity) very close to the top of the hill, and take an arbitrarily long time to roll down. There are also, of course, trajectories that have a substantial velocity near the top of the hill, which would inflate for a relatively short period of time. (Inflation only happens when the energy density is mostly in the form of the potential itself, with a minimal contribution from the kinetic energy caused by the field velocity.) So there is an interesting tradeoff, and we would like to know which effect wins.
The answer that Grant and I derived is: in the quadratic potential, we generically expect a huge amount of inflation, while in the cosine potential, we expect barely enough (fairly close to the hoped-for 50 e-folds). Although you can in principle inflate forever near a hilltop, such behavior is non-generic; you really need to fine-tune the initial conditions to make it happen. In the quadratic potential, by contrast, getting a buttload of inflation is no problem at all.
Of course, this entire analysis is done using the classical measure on trajectories through phase space. The actual world is not classical, nor is there any strong reason to expect that the initial conditions for the universe are randomly chosen with respect to the Liouville measure. (Indeed, we’re pretty sure that they are not.)
So this study has a certain aspect of looking-under-the-lamppost. We consider the naturalness of cosmological histories with respect to the conserved measure on classical phase space because that’s what we can do. If we had a finished theory of quantum gravity and knew the wave function of the universe, we would just look at that.
We’re not looking for blatant contradictions with data, we’re looking for clues that can help us move forward. The way to interpret our result is to say that, if the universe has a field with a potential like the quadratic inflation model (and the initial conditions are sufficiently smooth to allow inflation at all), then it’s completely natural to get more than enough inflation. If we have the cosine potential, on the other hand, than getting enough inflation is possible, but far from a sure thing. Which might be very good news — it’s generally thought that getting precisely “just enough” inflation is annoying finely-tuned, but here it seems quite plausible. That might suggest that we could observe remnants of the pre-inflationary universe at very large scales today.
hi, professor carroll, i have been thinking about AdS/CFT these days, I guess that the useful correspondence should be dS/QFT, and the two dimensional projection is the cosmic horizon. Is this right or reasonable? Am I right?
Haolin– Sorry, try to keep comments to the topic of the post. For other queries check out places like http://quora.com/Physics .
Professor,
For this much inflation you are proposing, what is the absolute amount of energy that was expended? And how much energy, in the same unit, is involved in a typical entanglement say between two photons?
KC
KC– I’m afraid those aren’t really well-defined questions. Energy isn’t conserved in general relativity (https://www.preposterousuniverse.com/blog/2010/02/22/energy-is-not-conserved/) and entanglement doesn’t necessarily involve any energy at all.
Sean – I seem to remember it being said (maybe here on this blog) that the Planck group was expected to release their paper in September, with the proper data and methods that would show whether or not the BICEP group had been justified in their claims of proof of inflation, or whether they’d got the foreground dust model wrong. I wanted to ask if you had heard any rumblings of whether or not we might get to see that Planck paper, and when, and whether we can expect it to settle the question. I’m terribly interested in finding out whether we’ve really seen proof of inflation writ large in the heavens.
Thanks for the link to the paper with 193 models. I wish the authors had shown simple graphs of all those potentials, like your two graphs, for the sake of visual comparison. I’m holding out for catenary inflation myself, for no good reason at all.
I haven’t kept track of the schedule for the Planck release. I’m sure we’ll know when it happens!
Sean,
What happens if, say, future observations were to rule out chaotic or eternal inflation and that ours is the only universe? How would scientists explain the cosmological constant and the fact that constants are “just right” for life?
Hey, are you two guys taking yourselves seriously?
If this is science, I’m Elvis.
And don’t say”Hi, Elvis!”
It does seem remarkable that phase space and attractors could possibly lead to explaining inflation. After reading your book, I am shocked that you would have even looked into something like that. It has been a while since I looked into it, but I found it fascinating that someone had actually made an alternate form of physics that was equally accurate. Then he developed these attractors to try to describe electronic interference in electrical devices that reflect electromagnetic waves. I actually thought about following up on that work one day when I become a physicist. It seemed like the universe could have exploded from such interference. It seems like I don’t have to adjust any of my pseudo-theories, that is always nice. Then it always seemed like it would be better to use what science we already have instead of trying to start from scratch. Maybe, physics isn’t that bad after all. It really seems to be at the top of the bar.
Sean: I think you should talk soon about the motivation for inflation. Because IMHO when you look at how the universe is flat, then wind back a billion years, then repeat, you appreciate it’s always been flat. And that inflation is totally superfluous. IMHO it’s all down to some issues with GR. For example, people say gravitational field energy is negative, but look at page 185 of the Doc30 Foundation of the General Theory of Relativity and Einstein says “the energy of the gravitational field shall act gravitatively in the same way as any other kind of energy”. It’s positive energy. And energy is conserved in general relativity. Imagine you send a 511keV photon into a black hole. The black hole mass increases by 511keV/c², no more. The blueshifted photon doesn’t actually gain any energy, it just looks as if it has because you lose it when you descend, in line with the mass deficit. Flip it round for redshift.
” … a buttload of inflation …”
There you go with the esoteric technical terminology again!
Dear Sean,
You are, I believe, making a Bayesian analysis of models of inflation? You calculate p(# e-folds | a theory of inflation), and find the expectation in the usual manner? Why not be explicit that your methodology is Bayesian in nature?
Wouldn’t the work be more credible if you made it clear it were grounded in the consistent, logical framework of Bayes?
I never quite grasped the full genius of the band known as Kansas, until now.
https://www.youtube.com/watch?v=tH2w6Oxx0kQ
“Dust In The Wind”
I close my eyes only for a moment, and inflation’s gone
My Nobel dreams pass before my eyes, a curiosity
Dust in the wind, all inflation is is dust in the wind
Same old song, just a drop of hype in the CMB
Inflation crumbles to the ground, though we refuse to see
Dust in the wind, all inflation is is dust in the wind
Now, don’t scrape slides, nothing lasts forever but the earth and sky
It slips away, and all your money won’t a primordial wave buy
Dust in the Linde, all inflation is is dust in the wind (all inflation is is dust in the wind)
Dust in the wind (inflation is dust in the Linde), inflation is dust in the wind (the wind)
So inflation was “created” to solve a few problems like flatness of the universe. But what if there is no evidence found to support this theory? Does science keep the theory around forever?
Maybe Sherlock Holmes adage needs to apply not matter how distasteful it might seem.
BTW just read today that someone claims to be able to prove black holes are impossible to happen. What is going on in the world of cosmology?
Hi sir, I am Sparsh. I am just a kid to Ask you that if expansion is explained by hubble law says in v = H*D where distance is between two galaxies or from earth… but if taken in very early universe (assume universe is 25 km in length), how can I calculate expansion if there is? Suppose at A point there electron and at point B ( 25 km away) there is another electron… in the same early universe… can I calculate the expanding space between them per sec?
And my second question is that can inflation have happened faster than speed of c? As it contains no info and doesn’t violent gen. Relativity or special
Thanks…!!!
I apologize for being off topic but this is related to your Sleeping Beauty post that no longer accepts comments.
That scenario is based on a 50 % chance for each outcome of heads or tails, or up or down, etc. , so that the universe splits in two, as you say, with equal amplitudes (1/root 2) (EQM). How does EQM reconcile the case for unequally weighted probabilities (or probability amplitudes)? For example, let’s prepare a two-level system like an unfair coin, with 80% chance of being up and 20% down.
What is different about the splitting process of the universe in this situation? In other words, how does the Everettian interpretation distinguish the varying probabilities of each outcome?