The question of how information escapes from evaporating black holes has puzzled physicists for almost forty years now, and while we’ve learned a lot we still don’t seem close to an answer. Increasingly, people who care about such things have been taking more seriously the intricacies of quantum information theory, and learning how to apply that general formalism to the specific issues of black hole information.
Now two students and I have offered a small contribution to this effort. Aidan Chatwin-Davies is a grad student here at Caltech, while Adam Jermyn was an undergraduate who has now gone on to do graduate work at Cambridge. Aidan came up with a simple method for getting out one “quantum bit” (qubit) of information from a black hole, using a strategy similar to “quantum teleportation.” Here’s our paper that just appeared on arxiv:
How to Recover a Qubit That Has Fallen Into a Black Hole
Aidan Chatwin-Davies, Adam S. Jermyn, Sean M. CarrollWe demonstrate an algorithm for the retrieval of a qubit, encoded in spin angular momentum, that has been dropped into a no-firewall unitary black hole. Retrieval is achieved analogously to quantum teleportation by collecting Hawking radiation and performing measurements on the black hole. Importantly, these methods only require the ability to perform measurements from outside the event horizon and to collect the Hawking radiation emitted after the state of interest is dropped into the black hole.
It’s a very specific — i.e. not very general — method: you have to have done measurements on the black hole ahead of time, and then drop in one qubit, and we show how to get it back out. Sadly it doesn’t work for two qubits (or more), so there’s no obvious way to generalize the procedure. But maybe the imagination of some clever person will be inspired by this particular thought experiment to come up with a way to get out two qubits, and we’ll be off.
I’m happy to host this guest post by Aidan, explaining the general method behind our madness.
If you were to ask someone on the bus which of Stephen Hawking’s contributions to physics he or she thought was most notable, the answer that you would almost certainly get is his prediction that a black hole should glow as if it were an object with some temperature. This glow is made up of thermal radiation which, unsurprisingly, we call Hawking radiation. As the black hole radiates, its mass slowly decreases and the black hole decreases in size. So, if you waited long enough and were careful not to enlarge the black hole by throwing stuff back in, then eventually it would completely evaporate away, leaving behind nothing but a bunch of Hawking radiation.
At a first glance, this phenomenon of black hole evaporation challenges a central notion in quantum theory, which is that it should not be possible to destroy information. Suppose, for example, that you were to toss a book, or a handful of atoms in a particular quantum state into the black hole. As the black hole evaporates into a collection of thermal Hawking particles, what happens to the information that was contained in that book or in the state of (what were formerly) your atoms? One possibility is that the information actually is destroyed, but then we would have to contend with some pretty ugly foundational consequences for quantum theory. Instead, it could be that the information is preserved in the state of the leftover Hawking radiation, albeit highly scrambled and difficult to distinguish from a thermal state. Besides being very pleasing on philosophical grounds, we also have evidence for the latter possibility from the AdS/CFT correspondence. Moreover, if the process of converting a black hole to Hawking radiation conserves information, then a stunning result of Hayden and Preskill says that for sufficiently old black holes, any information that you toss in comes back out almost a fast as possible!
Even so, exactly how information leaks out of a black hole and how one would go about converting a bunch of Hawking radiation to a useful state is quite mysterious. On that note, what we did in a recent piece of work was to propose a protocol whereby, under very modest and special circumstances, you can toss one qubit (a single unit of quantum information) into a black hole and then recover its state, and hence the information that it carried.
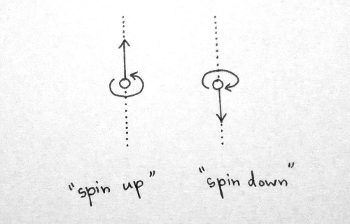
More precisely, the protocol describes how to recover a single qubit that is encoded in the spin angular momentum of a particle, i.e., a spin qubit. Spin is a property that any given particle possesses, just like mass or electric charge. For particles that have spin equal to 1/2 (like those that we consider in our protocol), at least classically, you can think of spin as a little arrow which points up or down and says whether the particle is spinning clockwise or counterclockwise about a line drawn through the arrow. In this classical picture, whether the arrow points up or down constitutes one classical bit of information. According to quantum mechanics, however, spin can actually exist in a superposition of being part up and part down; these proportions constitute one qubit of quantum information.
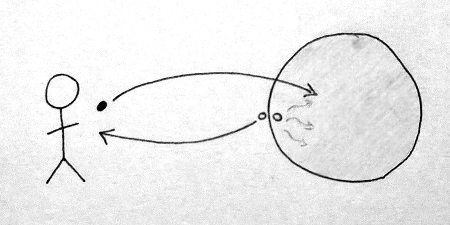
So, how does one throw a spin qubit into a black hole and get it back out again? Suppose that Alice is sitting outside of a black hole, the properties of which she is monitoring. From the outside, a black hole is characterized by only three properties: its total mass, total charge, and total spin. This latter property is essentially just a much bigger version of the spin of an individual particle and will be important for the protocol.
Next, suppose that Alice accidentally drops a spin qubit into the black hole. First, she doesn’t panic. Instead, she patiently waits and collects one particle of Hawking radiation from the black hole. Crucially, when a Hawking particle is produced by the black hole, a bizarro version of the same particle is also produced, but just behind the black hole’s horizon (boundary) so that it falls into the black hole. This bizarro ingoing particle is the same as the outgoing Hawking particle, but with opposite properties. In particular, its spin state will always be flipped relative to the outgoing Hawking particle. (The outgoing Hawking particle and the ingoing particle are entangled, for those in the know.)
The picture so far is that Alice, who is outside of the black hole, collects a single particle of Hawking radiation whilst the spin qubit that she dropped and the ingoing bizarro Hawking particle fall into the black hole. When the dropped particle and the bizarro particle fall into the black hole, their spins combine with the spin of the black hole—but remember! The bizarro particle’s spin was highly correlated with the spin of the outgoing Hawking particle. As such, the new combined total spin of the black hole becomes highly correlated with the spin of the outgoing Hawking particle, which Alice now holds. So, Alice measures the black hole’s new total spin state. Then, essentially, she can exploit the correlations between her held Hawking particle and the black hole to transfer the old spin state of the particle that she dropped into the hole to the Hawking particle that she now holds. Alice’s lost qubit is thus restored. Furthermore, Alice didn’t even need to know the precise state that her initial particle was in to begin with; the qubit is recovered regardless!
That’s the protocol in a nutshell. If the words “quantum teleportation” mean anything to you, then you can think of the protocol as a variation on the quantum teleportation protocol where the transmitting party is the black hole and measurement is performed in the total angular momentum basis instead of the Bell basis. Of course, this is far from a resolution of the information problem for black holes. However, it is certainly a neat trick which shows, in a special set of circumstances, how to “bounce” a qubit of quantum information off of a black hole.
Hello. Absolute layman here, but I have what may be a very rediculous question.
On the topic of teleportation, if you use intanglement, can you use that to import, or even share information back and forth into the black hole?
Also, thank you for the fascinating information you share, as well as the comprehensible way you impart it. You are very good at translating the esoteric to something just beyond what I can comprehend.
Brent– “Quantum teleportation” is a way to transfer a bit of quantum information, if the source and target share two particles that are entangled. That is basically what we are doing with our protocol. If you’re not sharing entangled particles, there’s no way to teleport.
You say: “Of course, this is far from a resolution of the information problem for black holes”. But I do not think you are too far.
Horowitz & Maldacena, in hep-th/0310281, already pointed out that idea of transfering “the information to the outgoing Hawking radiation in a process similar to ‘quantum teleportation’ “. But they required to “impose a final state boundary condition at black hole singularities”. If you lads, instead of that boundary condition, are capable of using the own gravitation field of the black hole (in a way like, e.g, Kiefer & Singh in P.R. D44 1067 in 1991), then you might be able to compute a general solution for the BH info paradox.
Does this (or must it) also conserve momentum?
I’m not sure I understand why you need to wait for any Hawking radiation at all. Is the information ever really inside the black hole in this protocol?
Suppose for simplicity that the initial angular momentum of the black hole is 0.
Now drop an electron in. The spin of the electron is never lost inside the horizon. Since angular momentum is conserved, it remains visible afterwards as the angular momentum of black hole, one of the few properties that are observable from outside. You can measure it any way you could measure the original electron’s spin, including performing a joint measurement with half of an EPR pair to teleport it to a new qbit.
I must be missing something, because it seems like Ralph Hartley’s suggestion would work but only if you measured the spin of the black hole before Alice dropped her particle in, and after anything else had fallen in. And the subsequent measurement of the black hole’s spin would only reveal the spin of Alice’s particle if measured before anything else fell in. But then it seems like the given protocol has the same issue except you don’t need the prior measurement of the black hole.
I guess what I’m saying is I don’t see the correlation between an arbitrary particle of Hawking Radiation and an arbitrary particle that previously fell into the black hole. Why is that outgoing particle correlated with Alice’s?
Or is that the limitation you were talking about? As soon as there is more than one qubit that has fallen into the black hole (ever?) it doesn’t work?
If you measure the spin of a qubit, the actual quantum information is lost — you only get an answer of the form “up” or “down.” What we’re trying to do here is retain all of the information (amplitudes and phases) of the original wave function.
I’m confused by the phrase “bizarro particle”, which is calmly used here as though it is standard physics terminology. That seemed unlikely to me, so I checked … and it brings up only five results on Google (of which this very blog post is number one). Probably not established terminology, then.
I really don’t see what purpose it serves. It sounds like the product of a mind that has decided strange quarks are too mundane — stranger than strange is bizarre, and stranger than bizzare is putting an “o” on the end of bizzare to emphasise just how bizarre it is. What’s next, Ridiculostrosity Particle? I found it distracting, and I can’t imagine how any hypothetical reader might find it an aid to understanding.
(P.S. For the record, I am not claiming legal protection on “ridiculostrosity particle”.)
Is the restriction to one qubit due to monogamous behavior of entanglement? Also does similar thought experiment with a qubit and ordinary black body radiating on earth work?
I very much enjoyed your paper. It is a straightforward, but very creative idea, which was very well framed. However, I couldn’t help but wonder if the entanglement of the Hawking radiation might loose some spin fidelity as it climbs out of the black hole. For example, in their paper “Quantum Entanglement of Moving Bodies” (http://arxiv.org/abs/quant-ph/0205179) Gingrich and Adami argue that entanglement over one measurable like spin or momentum alone isn’t a Lorentz invariant (e.g. as measured with the concurrence in that measurable) but that there is entanglement swapping between those sectors of the state vector as the system moves to different frames. However, it seems that your system assumes the Hawking radiation retains its angular momentum state as it frame-hops out of the black hole’s curvature to the external observer. The argument by Gingrich is made in the context of SR, but it seems clear similar ideas would equally apply in the context of GR. Just food for thought.
Throughout the article (and in comments), hypothetical “Hawking radiation” is mentioned and used as if it is now a scientifically established fact. When (in what paper) was this fact announced, how were the observations of said radiation obtained? It sounds like a major breakthrough, and I’m surprised that I cannot find any references to such an important achievement.
In quantum teleportation, you also need to send classical information in order to be able to reconstruct the initial state. If the analogy to teleportation holds water, it seems like you would sneed some classical information to be transmitted from the inside to the outside of the black hole. Is that correct?
Matt- Right. The classical information transfer is accomplished by measuring the black hole spin before and after.
It sounds like a much better way to explain away conservation of information for a black hole, since entanglement is faster than light. I heard Leonard Susskind conned Stephen Hawking into thinking that information wasn’t lost, because an object would be frozen on the surface of the black hole. This idea seems a little off to me. I was never aware that spacetime dilation could create a change in velocity of the object itself. You would think if you threw a watch in a black hole, just the hands on the watch would stop relative to another observer, not the watch itself.
Leonard Susskind would probably just say that the qubit never was able to go into the black hole in the first place, so you would just be getting information from the surface. Then it may have just been a bunch of hand waving anyways.
I have even heard of some physicist going back on the idea of not being able to go the speed of light due to a mass increase. That would be because it would only be a relative mass increase, and from the frame of reference of the object that was accelerating, it wouldn’t be able to detect it’s own mass increase. How do you end up with a fat and slow twin that still thinks he is skinny and runs marathons when your not looking?
Question: is there some kind of formal information conservation law in quantum physics that is missing from classical physics? And if so, why?
Suppose a bit is encoded in the sense of the angular momentum vector of a macroscopic top; or, alternatively, multiple bits are encoded in the value of that vector, to a given resolution. Now apply friction to annul the top rotation; the information stored in it is thereby lost, and in the environment there appears a certain increase in entropy, the value of which is presumably not necessarily precisely compensating for the lost information. (Is it?) And no shocking paradigmatic anomaly is declared.
So why is it unacceptable that a qubit be lost to the black hole entropy? And if there exist classical and quantum laws of information conservation, why aren’t they famous?
This is absurd! Stephen Hawking would never ride in a bus. He probably takes a chauffeured car and only flies privately. What about decoherence? Someone mentioned time dilation too. How can we measure information at the event horizon if it takes forever to get there? Why can they not use an ensemble? I wonder if a mini experiment on Earth could be used to see if entanglement is non-local (Bell’s theorem allows non-local hidden variables) in a gravitational field. If Alice and Bob experience time dilation due to being at different altitudes then is it possible that Bob who is at a lower elevation can collapse the wavefunction before Alice sees him perform the measurement? Is it possible to have an ensemble of entangled states that undergoes decoherence to create a macroscopic mixed state faster than message?
Thank you for taking time to read people’s comments and provide answers.
I am confused by the two uses of spin in this argument, the quantum spin of the infalling fermion and the macroscopic spin of the black hole. I was taught, at the U of Chicago!, that the quantum spin was a purely quantum property that behaved like classical angular momentum. Would this quantum spin affect the macroscopic rotation of the black hole? In the preprint paper, it is mentioned taking the spin measurement of the black hole, |m,j>; is this possible? I’ve always thought the spin of the black hole was a classical rotation. Would the infalling fermion also change the classical rotation of the black hole by some tiny tiny amount as well? And how could one measure accurately such a huge quantity? I suppose one could start with a non-rotating black hole and add the fermion at a perpendicular angle so there is no change to the classical angular momentum of the black hole. I apologize if these are dumb questions.
Gaehazzi- Good question! Conservation of quantum information follows from the axioms of quantum theory. In particular, if the time-evolution of a system is generated by a self-adjoint Hamiltonian (which quantum theory says is the case if you haven’t ignored any part of your system in its description), then you get conservation of information as a consequence. Of course, quantum theory is a theory; it could be that it needs to be modified for black holes. But, so far physicists have been rather successful at reconciling black holes and information, to the point that it’s much less attractive from a theoretical point of view to postulate destruction of quantum information.
Classical information is very different from quantum information, a major difference being that there is no corresponding conservation law. You’re on the right track when you talk about a corresponding increase in entropy in your example, though — check out the Wikipedia page on Landauer’s Principle, which talks about the thermodynamic cost of erasure.
Josh- Yes, the spin of an infalling particle will affect the angular momentum of a black hole, albeit by a tiny amount. Measuring the angular momentum of a black hole down to Planck-scale resolution is a formidable task, which does make the protocol quite impractical, but importantly, there are no fundamental barriers which would in principle prohibit any of the measurements that we describe.
You can do it in serial though, can’t you? Do the procedure on day one. Then toss in another qubit on day two. Etc. So maybe the trick to getting all the information in your book back is to digitize it into qubits and then toss your book in one quantum bit at a time.
Apologies if this is a dumb question. About the only result I remember from a course on black holes 20 odd years ago is that for an observer beyond the event horizon it takes an infinite amount of time to observe an infalling particle cross the event horizon (whereas for the particle itself it crosses the horizon and reaches the singularity in finite proper time). So in what sense can Alice perform any measurement after the particle has crossed the horizon?
I think there’s confusion about what probably is in a black hole. A star of ultra relativistic material smaller than the Schwarzschild radius shouldn’t collapse. Ultra-relativistic pressure (like conventional pressure) increases as the inverse of r-cubed, faster than the forces of gravity increase. Also black holes have measurable spin which imply a relatively large object within the Schwarzschild radius.
My calculation: The pressure P of ultra relativistic material is (rho)(c^2)/3, where rho is the energy density. The virial energy (thermal energy) of this mixture would be ∫PdV = M(c^2)/3. The gravitational binding energy of a star is about 1.1G(M^2)/R. Using the virial equation, IF M(c^2)/3 is equal to 1/2 of 1.1 G(M^2)/R, the radius R of this ultra relativistic material equals 1.65GM/(c^2), or 0.82 of the Schwarzschild radius.