The other day I was amused to find a quote from Einstein, in 1936, about how hard it would be to quantize gravity: “like an attempt to breathe in empty space.” Eight decades later, I think we can still agree that it’s hard.
So here is a possibility worth considering: rather than quantizing gravity, maybe we should try to gravitize quantum mechanics. Or, more accurately but less evocatively, “find gravity inside quantum mechanics.” Rather than starting with some essentially classical view of gravity and “quantizing” it, we might imagine starting with a quantum view of reality from the start, and find the ordinary three-dimensional space in which we live somehow emerging from quantum information. That’s the project that ChunJun (Charles) Cao, Spyridon (Spiros) Michalakis, and I take a few tentative steps toward in a new paper.
We human beings, even those who have been studying quantum mechanics for a long time, still think in terms of a classical concepts. Positions, momenta, particles, fields, space itself. Quantum mechanics tells a different story. The quantum state of the universe is not a collection of things distributed through space, but something called a wave function. The wave function gives us a way of calculating the outcomes of measurements: whenever we measure an observable quantity like the position or momentum or spin of a particle, the wave function has a value for every possible outcome, and the probability of obtaining that outcome is given by the wave function squared. Indeed, that’s typically how we construct wave functions in practice. Start with some classical-sounding notion like “the position of a particle” or “the amplitude of a field,” and to each possible value we attach a complex number. That complex number, squared, gives us the probability of observing the system with that observed value.
Mathematically, wave functions are elements of a mathematical structure called Hilbert space. That means they are vectors — we can add quantum states together (the origin of superpositions in quantum mechanics) and calculate the angle (“dot product”) between them. (We’re skipping over some technicalities here, especially regarding complex numbers — see e.g. The Theoretical Minimum for more.) The word “space” in “Hilbert space” doesn’t mean the good old three-dimensional space we walk through every day, or even the four-dimensional spacetime of relativity. It’s just math-speak for “a collection of things,” in this case “possible quantum states of the universe.”
Hilbert space is quite an abstract thing, which can seem at times pretty removed from the tangible phenomena of our everyday lives. This leads some people to wonder whether we need to supplement ordinary quantum mechanics by additional new variables, or alternatively to imagine that wave functions reflect our knowledge of the world, rather than being representations of reality. For purposes of this post I’ll take the straightforward view that quantum mechanics says that the real world is best described by a wave function, an element of Hilbert space, evolving through time. (Of course time could be emergent too … something for another day.)
Here’s the thing: we can construct a Hilbert space by starting with a classical idea like “all possible positions of a particle” and attaching a complex number to each value, obtaining a wave function. All the conceivable wave functions of that form constitute the Hilbert space we’re interested in. But we don’t have to do it that way. As Einstein might have said, God doesn’t do it that way. Once we make wave functions by quantizing some classical system, we have states that live in Hilbert space. At this point it essentially doesn’t matter where we came from; now we’re in Hilbert space and we’ve left our classical starting point behind. Indeed, it’s well-known that very different classical theories lead to the same theory when we quantize them, and likewise some quantum theories don’t have classical predecessors at all.
The real world simply is quantum-mechanical from the start; it’s not a quantization of some classical system. The universe is described by an element of Hilbert space. All of our usual classical notions should be derived from that, not the other way around. Even space itself. We think of the space through which we move as one of the most basic and irreducible constituents of the real world, but it might be better thought of as an approximate notion that emerges at large distances and low energies.
So here is the task we set for ourselves: start with a quantum state in Hilbert space. Not a random or generic state, admittedly; a particular kind of state. Divide Hilbert space up into pieces — technically, factors that we multiply together to make the whole space. Use quantum information — in particular, the amount of entanglement between different parts of the state, as measured by the mutual information — to define a “distance” between them. Parts that are highly entangled are considered to be nearby, while unentangled parts are far away. This gives us a graph, in which vertices are the different parts of Hilbert space, and the edges are weighted by the emergent distance between them.
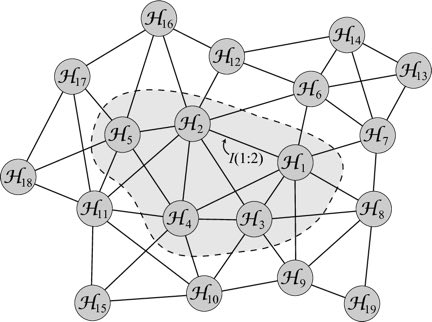
We can then ask two questions:
- When we zoom out, does the graph take on the geometry of a smooth, flat space with a fixed number of dimensions? (Answer: yes, when we put in the right kind of state to start with.)
- If we perturb the state a little bit, how does the emergent geometry change? (Answer: space curves in response to emergent mass/energy, in a way reminiscent of Einstein’s equation in general relativity.)
It’s that last bit that is most exciting, but also most speculative. The claim, in its most dramatic-sounding form, is that gravity (spacetime curvature caused by energy/momentum) isn’t hard to obtain in quantum mechanics — it’s automatic! Or at least, the most natural thing to expect. If geometry is defined by entanglement and quantum information, then perturbing the state (e.g. by adding energy) naturally changes that geometry. And if the model matches onto an emergent field theory at large distances, the most natural relationship between energy and curvature is given by Einstein’s equation. The optimistic view is that gravity just pops out effortlessly in the classical limit of an appropriate quantum system. But the devil is in the details, and there’s a long way to go before we can declare victory.
Here’s the abstract for our paper:
Space from Hilbert Space: Recovering Geometry from Bulk Entanglement
ChunJun Cao, Sean M. Carroll, Spyridon MichalakisWe examine how to construct a spatial manifold and its geometry from the entanglement structure of an abstract quantum state in Hilbert space. Given a decomposition of Hilbert space H into a tensor product of factors, we consider a class of “redundancy-constrained states” in H that generalize the area-law behavior for entanglement entropy usually found in condensed-matter systems with gapped local Hamiltonians. Using mutual information to define a distance measure on the graph, we employ classical multidimensional scaling to extract the best-fit spatial dimensionality of the emergent geometry. We then show that entanglement perturbations on such emergent geometries naturally give rise to local modifications of spatial curvature which obey a (spatial) analog of Einstein’s equation. The Hilbert space corresponding to a region of flat space is finite-dimensional and scales as the volume, though the entropy (and the maximum change thereof) scales like the area of the boundary. A version of the ER=EPR conjecture is recovered, in that perturbations that entangle distant parts of the emergent geometry generate a configuration that may be considered as a highly quantum wormhole.
Like almost any physics paper, we’re building on ideas that have come before. The idea that spacetime geometry is related to entanglement has become increasingly popular, although it’s mostly been explored in the holographic context of the AdS/CFT correspondence; here we’re working directly in the “bulk” region of space, not appealing to a faraway boundary. A related notion is the ER=EPR conjecture of Maldacena and Susskind, relating entanglement to wormholes. In some sense, we’re making this proposal a bit more specific, by giving a formula for distance as a function of entanglement. The relationship of geometry to energy comes from something called the Entanglement First Law, articulated by Faulkner et al., and used by Ted Jacobson in a version of entropic gravity. But as far as we know we’re the first to start directly from Hilbert space, rather than assuming classical variables, a boundary, or a background spacetime. (There’s an enormous amount of work that has been done in closely related areas, obviously, so I’d love to hear about anything in particular that we should know about.)
We’re quick to admit that what we’ve done here is extremely preliminary and conjectural. We don’t have a full theory of anything, and even what we do have involves a great deal of speculating and not yet enough rigorous calculating.
Most importantly, we’ve assumed that parts of Hilbert space that are highly entangled are also “nearby,” but we haven’t actually derived that fact. It’s certainly what should happen, according to our current understanding of quantum field theory. It might seem like entangled particles can be as far apart as you like, but the contribution of particles to the overall entanglement is almost completely negligible — it’s the quantum vacuum itself that carries almost all of the entanglement, and that’s how we derive our geometry.
But it remains to be seen whether this notion really matches what we think of as “distance.” To do that, it’s not sufficient to talk about space, we also need to talk about time, and how states evolve. That’s an obvious next step, but one we’ve just begun to think about. It raises a variety of intimidating questions. What is the appropriate Hamiltonian that actually generates time evolution? Is time fundamental and continuous, or emergent and discrete? Can we derive an emergent theory that includes not only curved space and time, but other quantum fields? Will those fields satisfy the relativistic condition of being invariant under Lorentz transformations? Will gravity, in particular, have propagating degrees of freedom corresponding to spin-2 gravitons? (And only one kind of graviton, coupled universally to energy-momentum?) Full employment for the immediate future.
Perhaps the most interesting and provocative feature of what we’ve done is that we start from an assumption that the degrees of freedom corresponding to any particular region of space are described by a finite-dimensional Hilbert space. In some sense this is natural, as it follows from the Bekenstein bound (on the total entropy that can fit in a region) or the holographic principle (which limits degrees of freedom by the area of the boundary of their region). But on the other hand, it’s completely contrary to what we’re used to thinking about from quantum field theory, which generally assumes that the number of degrees of freedom in any region of space is infinitely big, corresponding to an infinite-dimensional Hilbert space. (By itself that’s not so worrisome; a single simple harmonic oscillator is described by an infinite-dimensional Hilbert space, just because its energy can be arbitrarily large.) People like Jacobson and Seth Lloyd have argued, on pretty general grounds, that any theory with gravity will locally be described by finite-dimensional Hilbert spaces.
That’s a big deal, if true, and I don’t think we physicists have really absorbed the consequences of the idea as yet. Field theory is embedded in how we think about the world; all of the notorious infinities of particle physics that we work so hard to renormalize away owe their existence to the fact that there are an infinite number of degrees of freedom. A finite-dimensional Hilbert space describes a very different world indeed. In many ways, it’s a much simpler world — one that should be easier to understand. We shall see.
Part of me thinks that a picture along these lines — geometry emerging from quantum information, obeying a version of Einstein’s equation in the classical limit — pretty much has to be true, if you believe (1) regions of space have a finite number of degrees of freedom, and (2) the world is described by a wave function in Hilbert space. Those are fairly reasonable postulates, all by themselves, but of course there could be any number of twists and turns to get where we want to go, if indeed it’s possible. Personally I think the prospects are exciting, and I’m eager to see where these ideas lead us.
Exciting stuff — thanks for letting us peek over your shoulder like this!
This seems to me, as a layperson, very closely related to something I’ve been thinking a fair bit about recently.
If we are to take seriously that everything is waves, then there’s something big missing from all the for-the-lay-audience explanations of QM. Take the double-slit experiment: the electron wave diffracts past the slits; when it reaches the detector, magic happens. It might be the collapse of the wave function or the branching of the universe or whatever…
…but all those explanations only make sense if the detector is, itself, a monolithic classical (if not Platonic) entity.
But if it’s instead an assemblage of waves…then “detection” can only mean the interaction of one of the electron waves in the detector with the diffracted electron wave — a phosphorus atom absorbs the electron and spits it back out with a photon, a charge is induced in an element in the CCD array, whatever.
And if we assume that waves only interact when there’s some sort of interference pattern, and that the electron waves in the detector aren’t coherently synchronized, then it becomes mostly an anthropic matter as to which particular electron wave in the detector will be the one to first intersect with the diffracted electron wave. It would tend to happen more often when the diffracted electron wave is itself cresting, which is what we observe. And the particle-like nature of the observation is due entirely to the electron waves in the detector being tightly confined to very small locations.
I can’t be brilliant enough to be the first person to think of this, so I’m sure there must be something I’m missing…so can anybody point me in the right direction to understand where the mystery really lies?
Cheers,
b&
Hi Sean,
I was just reading your paper yesterday! Or tried to read it – I don’t think I really understood it :/ I have a question for you. If you’d take a different starting point, not by constructing space from the Hilbert-space by introducing a distance measure based on entanglement, but by instead defining space as that variable which makes a Hamiltonian local, would that pop out the metric as the thing necessary to contract the local terms? I’m wondering about this because this might tell you more about just what limit one is taking there and about the Hamiltonian rather than just the Hilbert space. (It might also help with the Lorentz-invariance issue.)
Best,
B.
No only do “We human beings, even those who have been studying quantum mechanics for a long time, still think in terms of a classical concepts.” but we tend to concretize things. Not only are wave functions mathematical abstractions, but they are one or more steps removed from any kind of reality at all. Using wave forms to describe electromagnetic waves has lead people to think the “waves” are objects rather than the fluctuations between two kinds of charges. I tried with college freshmen to do a thought experiment in which they were an electron and they would be grazed by EMR, being attracted and repelled in quick succession but even that got concretized. The waves were real to them as if the ether were back somehow and the idea of a supportive abstraction not connected to reality hadn’t yet become possible for them. It’s true for the gen pop, too I am afraid.
Still working my way through your book; still finding it fascinating.
Thanks for your blog!
Ben– Yes, the detector and slit and everything else in a double-slit experiments are ultimately quantum-mechanical, even if we often speak of them as classical. It’s a standard approximation, for objects that are not themselves interfering or exhibiting other quantum characteristics. I’m not sure where “anthropic” comes into the discussion, though. You might be thinking of the question of “pointer states,” which describe which quantum states systems decohere into.
Bee– Something like that might happen, it’s the kind of thing we’re looking into. But for this paper we don’t even have a Hamiltonian at all, since we’re just looking at states at a fixed time. That was an intentional choice, as frankly we’re not sure what the appropriate Hamiltonian would be.
History tells us that the solution to understanding all, inc gravitation will come by accident, and picked up by some
Observant person . Most future evolvement looked at. from say 100 years or 200 year backwards in time has shown that
Modern concepts of quantum as against classical is but a small but a jump fought over initially.
A digital or wave function universe is all we have at present.
Spacetime is digital or wave function, but the suggestion that it is digital but in rod forms, seems stupid or heretical .
The fight is between Edison and Tesla in its apparent propositions.
Both exceptional men , one dying in poverty and the other in affluence.
I know which tesla items I use each day.
Long live heretical thoughts.
This approach , if correct, takes away some of the mystery of non locality in Quantum Mechanics as evidenced for example in correlated measurement records in EPR type experiments. It’s a very attractive idea, and it might be right.
Sean,
What I’m driving at, I think…we can clearly see the crests and troughs of the wave of the electron that gets diffracted. Each electron in the detector is going to have similar crests and troughs, right? Only they’re tightly confined to the locations of their atoms.
If the crest of the diffracted electron wave reaches an electron in the detector when the detector’s electron’s wave is cresting, you presumably get constructive interference and an “observation.” But the electrons in the detector aren’t synchronized, right? So the individual electron closest to the slits might be at a minimum when the wave of the diffracted electron reaches it, so the two don’t interact. Rarely, none of the electrons in the bright part of the interference pattern are cresting at the right moment, and it’s one in the dark spots that happens to be cresting in such a way that the two can interact.
Or, put differently: what would you observe if the detector weren’t the traditional type, but, instead, a phosphorus-bearing molecule that had itself been sent through a double-slit diffraction?
Yet another way: what is the actual nature of the isolated interaction between the diffracted electron and the one spot on the detector where the observation actually happens? Not how that spot happened to be the one where the interaction took place; once whatever form of magic narrows it down to that particular site, what is it that happens at the site?
I’d bet a cup of coffee (but no more!) that a complete answer to what’s actually happening when the wave of the diffracted electron interacts with the wave of the single electron in the detector where the observation happens…that such a complete answer will also explain the proper interpretation of QM (Everett, Copenhagen, whatever). And I don’t at all think it’s a stretch to suggest that the “particle nature” of particles is due entirely to the fact that our detectors are manufactured in such a way as to confine their own particles’s waves to very small (atomic-scale) scales.
The old joke about the drunk looking for keys under the lamppost comes to mind…as I understand it, we’ve only ever tried to observe nature at that scale with devices that are themselves particle-like by design and construction. Can we, even in theory, design wave-like observers that’re as diffuse as the diffracted electrons themselves?
…keeping in mind, of course, that any cameras as well as our own eyes are, of necessity, going to resolve anything into points….
Cheers,
b&
Beware that space may be emergent while there is some aspect of time that is yet not emergent.
William Lane Craig will appeal to Occam’s razor against polytheism by postulating that “more things should not be used than are necessary”, and yet, Craig will not apply the same standard with respect to theism.
I can’t say that you’re on the right track or not, but keep going!
According to my understanding, entanglement is strictly independent of the physical distance between the two particles whereas gravity is strictly dependent on the distance. So it is surprising that gravity can emerge from your starting point of QM entanglement. If you were talking about CC it would be different.
“That complex number, squared, gives us the probability of observing the system with
that observed value.”
I really wish you wouldn’t do this. Surely anyone who knows what a complex number is can understand a norm. Say “the square of the magnitude of that complex number” if you have to.
It’s good to see more physicists thinking about finitism. Time to limit the influence of mathematics on physics. Get rid of zero, infinity, continuity. Use only discrete mathematics. More people are saying that we don’t have evidence of infinity in experience. Right. Now what about zero? Not even the vacuum is the absence of everything. It doesn’t happen. Yes, I have no bananas is not the same as zero bananas. No bananas is a temporal condition. Zero bananas is a mathematical condition, which is just fine in some systems, but not in reality. We have no experience of zero. No additive identity. If I have one banana and I add zero bananas, how many bananas do I have left? That’s nonsensical. No dividing by zero. Excludes infinities right away.
Thanks for the interesting post. I’m following this whole area closely—my training is in quantum information theory, so there’s at least one half of the arguments I’m able to understand.
I think an interesting precursor, at least in spirit, is the program due to C. F. v. Weizsäcker with his ‘ur theory’, originating sometime in the 50s I believe: to the best of my knowledge, he was the first to propose that space should emerge from the quantum, rather than there being some sort of quantization of gravity. His basic starting point was a reconstruction of what he called ‘abstract quantum theory’, that is, a theory not stemming from the quantization of some concrete system, but rather, an axiomatic framework based on the notion of his ‘ur alternative’ (which is basically a dichotomous measurement, a bit, or, in the quantum version, what would today be called a qubit), from which then everything else was supposed to be derived—space and time, gravitation, even particles and forces.
His argumentation was very heuristic at times, and he (and his collaborators) ultimately couldn’t carry the program through to completion, and it’s far from clear whether it’s possible at all; but I like to think of the modern approach as at least its spiritual successor. Unfortunately, much of the literature on this approach is in German; there does exist a recent English version of Weizsäcker’s Der Aufbau der Physik, as The Structure of Physics, translated by Holger Lyre and Thomas Görnitz, if you’re interested. Also, some papers of Lyre, such as this one, probably work as the best commonly-available introduction to (and, to some extent, continuation of) the program.
A book which covers time emerging from a hilbert space is “The end of time” by Julian Barbour which I found fascinating and seems to have some overlap with what you’re discussing. Also, doesn’t David Deutsch touch upon some of these ideas in his work too? I’ve found this general approach very alluring and would be great to see it all tie together, good luck with your future efforts!
How does this relate to work of Erik Verlinde?
Dear Sean, Is the electron spread out through space prior to measurement?
How these ideas relate to Manfred Requardt work, such as “Space-Time as an Orderparameter Manifold in Random Networks and the Emergence of Physical Points” (gr-qc 9902031) and subsequent articles? Some of them are quite recent, including some 2015 and 2016 papers.
what about “spin networks” and “spinors” and Penrose’s “twistors”
space IS quantized
not a physicist
Want another really crazy idea from yours truly? 😉 How about this:
Neither ordinary space-time nor Hilbert space are more or less fundamental than each other, but rather each is on an equal footing, as a *partial* explanation of reality.
If true, you could equally well reverse what the paper says, and show that Hilbert space is ’emergent’ from ordinary space-time ( a circular loop in reality).
Lets add ‘time’ to the mix as well, and say that that also can equally be taken as ‘fundamental’ or ’emergent’ – it’s purely a choice of which description you want to use.
There is a philosophical position known as ‘epistemological pluralism’ that supports this idea – rather than there being one universal explanation of reality, the idea is that there are only multiple partial explanations.
Sean, Two analogies support your position. #1. Michelangelo thinking of releasing David from the stone. He already had certain wave functions in mind. #2 and related is that stone that David was in is the center ball of a Newton’s cradle.
Andrea marsh on said here that History tells us that the solution to understanding all, inc gravitation will come by accident”
Well I won’t go for “by accident”, I like “by thinking” is better.
If this article is wrong, can anybody tell me then why we see a star in a place where it was million of years ago?
Something else, about super nova, why “gravity” gets aggressive only when (fuel finishes)?
I’m sure that gravity itself also till now wrong explained.
You can read this article about light here: https://waseinsteinwrong.wordpress.com/2016/07/17/annie-parker-vs-einstein/
Fine, but still loose ends remain
To elaborate on my ‘epistemological pluralism’ idea:
You have 3 entities here: Space, Hilbert Space and Time
My hypothesis is that you could pick any two as ‘fundamental’ and then derive the third one as ’emergent’. It’s all a big circular loop with 3 partial explanations of reality.
So you could have:
(1) Hilbert Space + Time = Space
(2) Space + Time = Hilbert Space
(3) Hilbert Space+ Space = Time
Your paper is about (1), so if I’m right, you need to have time as ‘fundamental’ to derive ordinary space. But I’m suggesting that whether something is ‘fundamental’ or ’emergent’ is purely a choice of description. If you want to derive time as ’emergent’, then you can go with (3).
The EPR paradox rests on the notion that far-apart entangled entities violate the finiteness of the speed of light. If spatial distance is redefined as related to the level of entanglement, the paradoxal nature of EPR might just go away. (Tightly entangled entities are as near as appropriate, regardless of the conventional distance between them.) Is that so in the CCM idea? And if so, what’s the nature of the emergent speed of light?
Fascinating stuff Sean. Does this imply that entaglement cannot be conserved over arbitrarily large distances ?