Usually, technical advances in mathematical physics don’t generate a lot of news buzz. But last year a story in Quanta proved to be an exception. It relayed the news of an intriguing new way to think about quantum field theory — a mysterious mathematical object called the Amplituhedron, which gives a novel perspective on how we think about the interactions of quantum fields.
 This is cutting-edge stuff at the forefront of modern physics, and it’s not an easy subject to grasp. Natalie Wolchover’s explanation in Quanta is a great starting point, but there’s still a big gap between a popular account and the research paper, in this case by Nima Arkani-Hamed and Jaroslav Trnka. Fortunately, Jaroslav is now a postdoc here at Caltech, and was willing to fill us in on a bit more of the details.
This is cutting-edge stuff at the forefront of modern physics, and it’s not an easy subject to grasp. Natalie Wolchover’s explanation in Quanta is a great starting point, but there’s still a big gap between a popular account and the research paper, in this case by Nima Arkani-Hamed and Jaroslav Trnka. Fortunately, Jaroslav is now a postdoc here at Caltech, and was willing to fill us in on a bit more of the details.
“Halfway between a popular account and a research paper” can still be pretty forbidding for the non-experts, but hopefully this guest blog post will convey some of the techniques used and the reasons why physicists are so excited by these (still very tentative) advances. For a very basic overview of Feynman diagrams in quantum field theory, see my post on effective field theory.
I would like to thank Sean to give me an opportunity to write about my work on his blog. I am happy to do it, as the new picture for scattering amplitudes I have been looking for in last few years just recently crystalized in the object we called Amplituhedron, emphasizing its connection to both scattering amplitudes and the generalization of polyhedra. To remind you, “amplitudes” in quantum field theory are functions that we square to get probabilities in scattering experiments, for example that two particles will scatter and convert into two other particles.
Despite the fact that I will talk about some specific statements for scattering amplitudes in a particular gauge theory, let me first mention the big picture motivation for doing this. Our main theoretical tool in describing the microscopic world is Quantum Field Theory (QFT), developed more than 60 years ago in the hands of Dirac, Feynman, Dyson and others. It unifies quantum mechanics and special theory of relativity in a consistent way and it has been proven to be an extremely successful theory in countless number of cases. However, over the past 25 years there has been an increasing evidence that the standard definition of QFT using Lagrangians and Feynman diagrams does not exhibit simplicity and sometimes even hidden symmetries of the final result. This has been most dramatically seen in calculation of scattering amplitudes, which are basic objects directly related to probabilities in scattering experiments. For a very nice history of the field look at the blog post by Lance Dixon who recently won together with Zvi Bern and David Kosower the Sakurai prize. There are also two nice popular articles by Natalie Wolchover – on the Amplituhedron and also the progress of understanding amplitudes in quantum gravity.
The Lagrangian formulation of QFT builds on two pillars: locality and unitarity, which means that the particle interactions are point-like and sum of the probabilities in scattering experiments must be equal to one. The underlying motivation of my work is a very ambitious attempt to reformulate QFT using a different set of principles and see locality and unitarity emerge as derived properties. Obviously I am not going to solve this problem but rather concentrate on a much simpler problem whose solution might have some features that can be eventually generalized. In particular, I will focus on on-shell (“real” as opposed to “virtual”) scattering amplitudes of massless particles in a “supersymmetric cousin” of Quantum Chromodynamics (theory which describes strong interactions) called N=4 Super Yang-Mills theory (in planar limit). It is a very special theory sometimes referred as “Simplest Quantum Field Theory” because of its enormous amount of symmetry. If there is any chance to pursue our project further we need to do the reformulation for this case first.
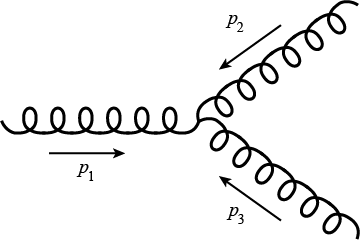
Feynman diagrams give us rules for how to calculate an amplitude for any given scattering process, and these rules are very simple: draw all diagrams built from vertices given by the Lagrangian and evaluate them using certain rules. This gives a function M of external momenta and helicities (which is spin for massless particles). The Feynman diagram expansion is perturbative, and the leading order piece is always captured by tree graphs (no loops). Then we call M a tree amplitude, which is a rational function of external momenta and helicities. In particular, this function only depends on scalar products of momenta and polarization vectors. The simplest example is the scattering of three gluons,
![]()
represented by a single Feynman diagram.
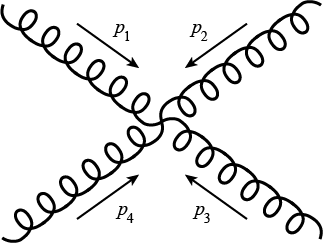
Amplitudes for more than three particles are sums of Feynman diagrams which have internal lines represented by factors P^2 (where P is the sum of momenta) in the denominator. For example, one part of the amplitude for four gluons (2 gluons scatter and produce another 2 gluons) is
![]()
Higher order corrections are represented by diagrams with loops which contain unfixed momenta – called loop momenta – we need to integrate over, and the final result is represented by more complicated functions – polylogarithms and their generalizations. The set of functions we get after loop integrations are not known in general (even for lower loop cases). However, there exists a simpler but still meaningful function for loop amplitudes – the integrand, given by a sum of all Feynman diagrams before integration. This is a rational function of helicities and momenta (both external and loop momenta) and it has many nice properties which are similar to tree amplitudes. Tree amplitudes and Integrand of loop amplitudes are objects of our interest and I will call them just “amplitudes” in the rest of the text.
While we already have a new picture for them, we can use the top-bottom approach and phrase the problem in the following way: We want to find a mathematical question to which the amplitude is the answer.
As a first step, we need to characterize how the amplitude is invariantly defined in a traditional way. The answer is built in the standard formulation of QFT: the amplitude is specified by properties of locality and unitarity, which translate to simple statements about poles (these are places where the denominator goes to zero). In particular, all poles of M must be sums of external (for integrand also loop) momenta and on these poles M must factorize in a way which is dictated by unitarity. For large class of theories (including our model) this is enough to specify M completely. Reading backwards, if we find a function which satisfies these properties it must be equal to the amplitude. This is a crucial point for us and it guarantees that we calculate the correct object.
Now we consider completely unrelated geometry problem: we define a new geometrical shape – the Amplituhedron. It is something like multi-dimensional polygon embedded in a particular geometrical space, called the Grassmannian. This has a very good motivation in the work done by me and my collaborators in last 5 years on relation between Grassmannians and amplitudes, but I will not explain it here in more details as it would need a separate blog post. Importantly, we can prove that the expression we get for a volume of this object satisfies properties mentioned above and therefore, we can conclude that the scattering amplitudes in our theory are directly related to the volume of Amplituhedron.
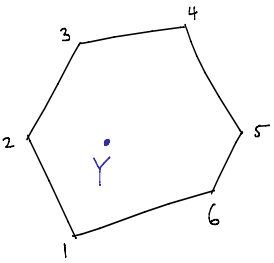 This is a basic picture of the whole story but I will try to elaborate it a little more. Many features of the story can be show on a simple example of polygon which is also a simple version of Amplituhedron. Let us consider n points in a (projective) plane and draw a polygon by connecting them in a given ordering. In order to talk about the interior the polygon must be convex which puts some restrictions on these n vertices. Our object is then specified as a set of all points inside a convex polygon.
This is a basic picture of the whole story but I will try to elaborate it a little more. Many features of the story can be show on a simple example of polygon which is also a simple version of Amplituhedron. Let us consider n points in a (projective) plane and draw a polygon by connecting them in a given ordering. In order to talk about the interior the polygon must be convex which puts some restrictions on these n vertices. Our object is then specified as a set of all points inside a convex polygon.
Now, we want to generalize it to Grassmannian. Instead of points we consider lines, planes, and in general k-planes inside a convex hull (generalization of polygon in higher dimensions). The geometry notion of being “inside” does not really generalize beyond points but there is a precise algebraic statement which directly generalizes from points to k-planes. It is a positivity condition on a matrix of coefficients that we get if we expand a point inside a polygon as linear combination of vertices. In the end, we can define a space of Amplituhedron in the same way as we defined a convex polygon by putting constraints on its vertices (which generalizes convexity) and also positivity conditions on the k-plane (which generalizes notion being inside). In general, there is not a single Amplituhedron but it is rather labeled by three indices: n,k,l. Here n stands for the number of particles, which is equal to a number of vertices, index k captures the helicity structure of the amplitude and it defines a dimensionality of a k-plane which defines a space. Finally, l is the number of loops which translates to the number of lines we have in our configuration space in addition to the k-plane. In the next step we define a volume, more precisely it is a form with logarithmic singularities on the boundaries of this space, and we can show that this function satisfies exactly the same properties as the scattering amplitude. For more details you can read our original paper.
This is a complete reformulation we were looking for. In the definition we do not talk about Lagrangians, Feynman diagrams or locality and unitarity. Our definition is purely geometrical with no reference to physical concepts which all emerge from the shape of Amplituhedron.
Having this definition in hand does not give the answer for amplitudes directly, but it translates the physics problem to purely math problem – calculating volumes. Despite the fact that this object has not been studied by mathematicians at all (there are recent works on the positive Grassmannian of which the Amplituhedron is a substantial generalization), it is reasonable to think that this problem might have a nice general solution which would provide all-loop order results.
There are two main directions in generalization of this story. The first is to try to extend the picture to full (integrated) amplitudes rather than just an integrand. This would definitely require more complicated mathematical structures as would deal now with polylogarithms and their generalizations rather than rational functions. However, already now we have some evidence that the story should extend there as well. The other even more important direction is to generalize this picture to other Quantum field theories. The answer is unclear but if it is positive the picture would need some substantial generalization to capture richness of other QFTs which are absent in our model (like renormalization).
The story of Amplituhedron has an interesting aspect which we always emphasized as a punchline of this program: emergence of locality and unitarity from a shape of this geometrical object, in particular from positivity properties that define it. Of course, amplitudes are local and unitary but this construction shows that these properties might not be fundamental, and can be replaced by a different set of principles from which locality and unitarity follow as derived properties. If this program is successful it might be also an important step to understand quantum gravity. It is well known that quantum mechanics and gravity together make it impossible to have local observables. It is conceivable that if we are able to formulate QFT in the language that does not make any explicit reference to locality, the weak gravity limit of the theory of quantum gravity might land us on this new formulation rather than on the standard path integral formulation. This would not be the first time when the reformulation of the existing theory helped us to do the next step in our understanding of Nature. While Newton’s laws are manifestly deterministic, there is a completely different formulation of classical mechanics – in terms of the principle of the least action – which is not manifestly deterministic. The existence of these very different starting points leading to the same physics was somewhat mysterious to classical physicists, but today we know why the least action formulation exists: the world is quantum-mechanical and not deterministic, and for this reason, the classical limit of quantum mechanics can’t immediately land on Newton’s laws, but must match to some formulation of classical physics where determinism is not a central but derived notion. The least action principle formulation is thus much closer to quantum mechanics than Newton’s laws, and gives a better jumping off point for making the transition to quantum mechanics as a natural deformation, via the path integral.
We may be in a similar situation today. If there is a more fundamental description of physics where space-time and perhaps even the usual formulation of quantum mechanics don’t appear, then even in the limit where non-perturbative gravitational effects can be neglected and the physics reduces to perfectly local and unitary quantum field theory, this description is unlikely to directly reproduce the usual formulation of field theory, but must rather match on to some new formulation of the physics where locality and unitarity are derived notions. Finding such reformulations of standard physics might then better prepare us for the transition to the deeper underlying theory.
I’m sorry but I didn’t understand this. Even “the scattering of three gluons” caused me an issue, because it says here that the gluons in ordinary hadrons are virtual, which doesn’t tie in with “the focus on on-shell (‘real’ as opposed to ‘virtual’) scattering amplitudes”. I tried reading the paper, but got as far as page 4 before deciding I was totally lost. So I’m none the wiser. Do other readers understand it?
Great this sentence on the top:
in truth, only atoms and the void.
In this void time is duration of atoms motion.
Eternity is NOW.
John D– The theory being studied, N=4 Super Yang-Mills, is different from ordinary QCD in a number of ways (although they both contain gluons). In particular, there are no “ordinary hadrons” in N=4 SYM, because the crucial property of confinement is lacking. So studying “real” gluons is a sensible thing to do. (You could still do it in ordinary QCD, it just wouldn’t tell you much about the real world.)
Thanks Jaroslav for this introduction to you and your colleague’s work. It seems an ambitious and exciting idea and I do wish you well. But while it remains focused on non-real world models there will be the worry that all of this is just beautiful pure mathematics rather than useful physics. We do have many stunning examples in history of pure mathematical ideas stimulating Physics advancement (Maxwell, Einstein(!), Dirac(!!) etc etc… ) and I will certainly be applauding if your geometrical model for calculating amplitudes becomes applicable to Nature.
btw (After Milner) I hope Nima is paying any bar/restaurant bills from now on 😉
Sean, thanks for getting back to me, but now it seems to be even more removed from actual physics. It’s like a hypothesis on the back of a speculation riding a conjecture. And I am none the wiser. Am I allowed to say Emperor’s New Clothes?
You’re allowed to say whatever you want. But the tradition in physics of looking at simplified toy models to get a better understanding goes back to Galileo, and is unlikely to be abandoned any time soon.
Sean – You say ” there are no “ordinary hadrons” in N=4 SYM, because the crucial property of confinement.”
That doesn’t make sense to me. There is confinement in QCD but there are ordinary hadrons. Are you sure you didn’t mean some other property of SYM or is the confinement in SYM different in some essential way?
My instinct is that on-shell gluon scattering amplitudes are physically meaningful for high-energy QCD processes where the free gluons eventually end up as jets, but I’m no particle physicist. It’s true that they mean nothing for Hadrons, but those are bound states – what could ‘scattering’ possibly mean? But that doesn’t mean they don’t mean anything
This is a beautiful mathematical development; however, I would like to point you to the recent breakthrough motivated by your original work:
The Realineituhedron!
Mike– Sorry, I meant “the crucial property of confinement is lacking.” N=4 SYM is “conformal” — invariant under changes of scale — so there is no energy scale with which particles can be confined, unlike the QCD scale of the real world.
This is a beautiful project. I love the thinking here. Reformulation of current theory (QFT) -> deformation of current theory -> new theory. I have been thinking about how to make breakthroughs in physics. So this very deep and historical way of approaching the problem of quantum gravity is impressive to me. The results connect geometry with QFT. Which is surprising. In a good way (smells like general relativity)…
Do I understand right that since you say ” In the next step we define a volume, more precisely it is a form with logarithmic singularities on the boundaries of this space” singularities in your method are not as bothersome as usual Feynman calculations? What happens in your method when you have non-renormalizable QFT ?
Just short comment on N=4 SYM vs QCD: We study N=4 SYM because it is a toy model for gauge theories. It has infinite dimensional symmetry and this makes the results simpler than in QCD. Despite this fact it is still fully interacting 4-dimensional QFT and the perturbative expansion is highly non-trivial. For example, tree-level amplitudes of gluons in N=4 SYM and QCD are identical. Indeed, there are no hadrons in this theory and the only states are gluons and superpartners, unlike in QCD where at low energies the physical degrees of freedom are different. However, at high energies gluonic interactions dominate even in QCD.
kashyap — We do not know. We did this geometric reformulation for this particular case of planar N=4 SYM. In fact, it was done in two steps: first we found new building blocks for amplitudes in this theory, so called on-shell diagrams, and then we found this unified object – Amplituhedron. We do not know how to do the second step in any other theory so far, but we partially understand the first step for larger class of theories – for N<4 or pure Yang-Mills theory. This theory is renormalizable but it is not conformal and the simplicity we see for N=4 SYM is absent. The challenge is to formulate amplitudes in pure Yang-Mills theory in a similar way we did for its maximal supersymmetric version. Pushing the story to non-renormalizable theories is even more complicated and I do not know how to even start at this moment.
Dr. Trnka: Thanks for your reply.Good luck with your efforts. I am still trying to understand qualitatively the difference between your techniques and those of Zvi Bern, Lance Dixon, and David Kosower. I understand they actually calculated QCD processes at LHC energy . Since you are going back to toy model SYM, it must be that you want to do much more. Can you say little bit about this. What will your technique achieve when it is successful for QCD?
kashyap — Our approach is quite different from work by Bern, Dixon, Kosower and others. They use traditional formulation of QFT, they just do it in much smarter way than the standard Feynman diagrams approach. Instead of Feynman diagrams they use a basis of scalar and tensor integrals, then imposing on-shell conditions (the loop amplitude factorizes into trees when you cut some of the internal propagators) they are able to fix these coefficients. This is a very nice general approach that works beyond N=4 SYM and it is very efficient to get also QCD calculations done. The Amplituhedron is not like that at all, it defines the amplitude independently on the standard QFT procedure as the volume of a generalization of convex polytopes to Grassmannians. It is a conceptually new definition and its primary purpose was not to make computations more efficient but to reformulate the QFT definition of scattering amplitudes. As for the actual calculations are concerned, we translated the physics problem to purely math problem of calculating volume of this space. We do not know how to calculate these things at the moment (just for some cases we do) but once it is understood how to do it in general, you get access to answers to all loop orders, which is something totally inaccessible from the standard approach. I do not know what the story is for QCD but if there is some new formulation of amplitudes there and we can fully understand it, then we would have the full perturbative series under control which is something extremely interesting. Of course, in QCD we have to consider also non-perturbative effects which would bring additional structure there.
Thanks Dr. Trnka for your very detailed and clarifying reply. I understand, in the beginning before a major breakthrough there are always great problems. It will be great when this approach is successful for both perturbative and non-perturbative QCD and perhaps even quantum gravity.
Is there a description of the Amplituhedron in the D-instanton expansion of the topological B model with target space $CP^{3|4}$?
I had an imprecise question – is there any chance that this can be extended/generalized to 3D Chern-Simons theory? Or is this a future goal that hasn’t yet been realized?
(I’m a mathematician, so I don’t really know what Chern-Simons theory is, but I study knot theory, and so I have heard some things about it. In particular I’d be curious whether the amplituhedron, or a related construction, could be used to construct knot invariants.)
Dear Jaroslav,
Thanks for the interesting post. Certainly the work on the amplituhedron is very impressive and for me as a combinatorialist and convex polytope researcher it is nice to see this type of mathematics plays a role in physics computations and foundations. I have two remarks/questions.
The first question is quite simple on the mathematics side: The positive grassmanian can be defined quite simply. You consider all n by m real matrices (m>n) with all n by n minors non-negative and give it a cell structure according to the signs of the n by n minors. (These signs are taken from the set {0,+}.) In other words, two matrices A and B are in the same (open) cell if for every n by n minor of A with vanishing determinant also the corresponding minor of B has vanishing determinant.
Now, the amplituhedron is described as an extension of the positive Grassmanian analogous to the way “triangles” are replaced with “polygons.” Is there a simple way to explain in a little more detail what the amplituhedron, as a geometric-mathematical object is? (I asked about it in matheoverflow and also Joe O’Rourke asked a similar question) but I cannot say I understand the situation and also not the analogy of moving from a triangle to a polygon and from a simplex to a general polytope. It seems that there should be an explanation not much more complicated than the one for the positive grassmanian.
The second remark/question is regarding the emergence of unitarity and locality. Sometimes physicists like to flirt with the idea that QM is actually an “effective theory” emerging from a more fundamental theory, where an especially bold version of this thought is that this “more fundamental theory” will actually falsify some QM predictions (in a similar way to the way predictions of Newtonian mechanics are falsified by quantum mechanics and relativity). Of course, there is nothing wrong with such flirting. Some of the explanations of your vision here in the blog and in some lectures by Nima Arkani-Hemed
I don’t think this is plausible interpretation of the amplituhedron work. We have here an approximation/computation method to describe a quantum system restricted to a small number of “degrees-of-freedom”. The simplest and least dramatic explanation of the emergence of unitarity and locality is that the emergence of unitarity and locality simply reflects and identifies situations where the approximation method is successful. So it corresponds to unitarity “emerging from quantum noise (or decoherence,)” (namely the effect of ignored degrees of freedom), and not from a “more fundamental” theory which, in some regimes, falsifies QM. Does this more mundane interpretation of the emergence of unitarity/locality seem reasonable to you?
(And one question for Sean: I noticed that in old archived posts of your blog the entire discussion threads vanish. Are they backed up somewhere?)
kneemo — Indeed, this is a correspondence with amplitudes in N=4 SYM that Edward Witten found in his paper from 2003 on twistor string theory. If you ask on the relation of Amplituhedron and twistor string theory — that is a great question but we do not have an answer to it. We can prove that the contours lead to positive matrices on the Amplituhedron side, however deeper understanding is still missing.
Peter — there is a good 3-dimensional candidate one should try to extend these ideas to and it is ABJM theory which is 3d Chern-Simons theory coupled to matter fields. There is already an on-shell diagram formulation of this theory (which was the first step in our construction for N=4 SYM) and I am sure people are looking now at the similar geometric construction similar to Amplituhedron.
Dear Gil,
thanks for your insightful questions. Let me try to answer them:
1) There is a very simple definition of the Amplituhedron which indeed involves the Positive Grassmannian. In fact, it is the map from G_+(k,n) -> G(k,k+4). The map is defined as Y = C.Z where C is the top cell of G_+(k,n), Z is the constant (k+4)x(n) positive matrix and Y is a subspace of G(k,k+4). On this space we define a form with logarithmic singularities on the boundaries and the amplitude can be extracted directly from this form. Here the labels n,k label the tree-level amplitudes in N=4 SYM. There is an extension for the loop integrand which involves additional objects. In particular, in addition to this k-plane (described by G(k,k+4)) we have also L lines that do not intersect this plane. These lines are again described by positive Grassmannians but in a little non-trivial way as there are also mutual positivity conditions between them.
2) The Amplituhedron is a statement about amplitudes in N=4 SYM and it does not tell you directly anything about quantum gravity. We work strictly in QFT framework and of course, the amplitudes we are getting are local and unitary. The interesting point here is that these properties are not fundamental but rather derived ones from this geometric construction. Locality and unitarity as postulates were replaced by some other set of postulates which have purely geometric origin. Of course, the final result for amplitudes is identical in both situations. At this point we do not falsify QM or anything else, it is just a reformulation and the Amplituhedron is only about that. The extra ideas about possible applications to quantum gravity are more speculative and are based on the fact that the emergence of spacetime and absence of local observables is a deep problem in combining QFT and gravity. Here we have a formulation of QFT (for this particular theory) which does not rely explicitly on locality so it is suggestive that it might be useful in thinking about quantum gravity. And there is this analogy with principle with least action. However, it can also happen that our construction will be later understood purely in physics terms and there will be no signs of possible connections to quantum gravity. The main result is in the other way of thinking about field theory and we will see in the future if this goes further or not.
Jaroslav,
Thank you very much for this post. I intend to follow progress as much as I can on the amplituhedron, which is a fresh and exciting idea that seems to show much promise. While I have no training in maths or physics, I’ve been enjoying Professor Arkani Hamed’s lectures online a great deal. In his lectures, as best I understand, Nima (if I may be informal) motivates this line of work by emphasizing advancements in a theory of the world as a hologram, which are described as extensions of well understood physics; ie., there are no local observables, black hole entropy goes like the area rather than the volume. Thus there is no [necessary] “inside” of space-time. Further, that challenges to our understanding of fundamental physics are “even worse” than not being able to build an experiment to detect physics at the planck length, that the challenges are cosmological — we live in an accelerating universe which came from a big bang meaning we have inherent limits on what we can observe and the specific kind of space time that must emerge, which does at a staggeringly low value for lambda. I have an inkling for the immensity of these problems for physics, but I don’t grasp how the amplituhedron is even possibly a signpost to a road to an answer. I do understand that unitarity and locality emerge as properties of the amplituhedron when calculating its volume. that is profoundly interesting. But how even in principle would it be possible to get from a geometry of scattering amplitudes – even if you were to find the amplituhedron for the whole standard model – to emergent space-time with properties of inflation and lambda for the whole universe? Of course it would be already tremendously exciting if you were able to solve for all loop amplitudes in N=4 let alone N=8, so solving these cosmological questions seems well beyond the horizon. Yet Nima uses them to motivate the work on the amplituhedron, so it is why I ask.
Also a much smaller question – have mathematicians started to work more vigorously on the positive grassmanian, from their own angles (no pun intended), as a result of your work? I wonder about how ‘purely’ mathematical probing might yield insights into the physics side.
Thanks very much!
This is slightly reminiscent of some work I did with John Baez and Dan Christensen, in which (the asymptotic values of) certain amplitudes in a model of quantum gravity could be found as integrals of an inverse volume of a tetrahedron.
One example is equation (27) in http://arxiv.org/abs/gr-qc/0208010 but there were other amplitude integrals with a broadly similar structure that we didn’t publish.