I have often talked about the Many-Worlds or Everett approach to quantum mechanics — here’s an explanatory video, an excerpt from From Eternity to Here, and slides from a talk. But I don’t think I’ve ever explained as persuasively as possible why I think it’s the right approach. So that’s what I’m going to try to do here. Although to be honest right off the bat, I’m actually going to tackle a slightly easier problem: explaining why the many-worlds approach is not completely insane, and indeed quite natural. The harder part is explaining why it actually works, which I’ll get to in another post.
Any discussion of Everettian quantum mechanics (“EQM”) comes with the baggage of pre-conceived notions. People have heard of it before, and have instinctive reactions to it, in a way that they don’t have to (for example) effective field theory. Hell, there is even an app, universe splitter, that lets you create new universes from your iPhone. (Seriously.) So we need to start by separating the silly objections to EQM from the serious worries.
The basic silly objection is that EQM postulates too many universes. In quantum mechanics, we can’t deterministically predict the outcomes of measurements. In EQM, that is dealt with by saying that every measurement outcome “happens,” but each in a different “universe” or “world.” Say we think of Schrödinger’s Cat: a sealed box inside of which we have a cat in a quantum superposition of “awake” and “asleep.” (No reason to kill the cat unnecessarily.) Textbook quantum mechanics says that opening the box and observing the cat “collapses the wave function” into one of two possible measurement outcomes, awake or asleep. Everett, by contrast, says that the universe splits in two: in one the cat is awake, and in the other the cat is asleep. Once split, the universes go their own ways, never to interact with each other again.
And to many people, that just seems like too much. Why, this objection goes, would you ever think of inventing a huge — perhaps infinite! — number of different universes, just to describe the simple act of quantum measurement? It might be puzzling, but it’s no reason to lose all anchor to reality.
To see why objections along these lines are wrong-headed, let’s first think about classical mechanics rather than quantum mechanics. And let’s start with one universe: some collection of particles and fields and what have you, in some particular arrangement in space. Classical mechanics describes such a universe as a point in phase space — the collection of all positions and velocities of each particle or field.
What if, for some perverse reason, we wanted to describe two copies of such a universe (perhaps with some tiny difference between them, like an awake cat rather than a sleeping one)? We would have to double the size of phase space — create a mathematical structure that is large enough to describe both universes at once. In classical mechanics, then, it’s quite a bit of work to accommodate extra universes, and you better have a good reason to justify putting in that work. (Inflationary cosmology seems to do it, by implicitly assuming that phase space is already infinitely big.)
That is not what happens in quantum mechanics. The capacity for describing multiple universes is automatically there. We don’t have to add anything.
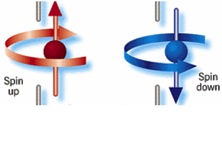The reason why we can state this with such confidence is because of the fundamental reality of quantum mechanics: the existence of superpositions of different possible measurement outcomes. In classical mechanics, we have certain definite possible states, all of which are directly observable. It will be important for what comes later that the system we consider is microscopic, so let’s consider a spinning particle that can have spin-up or spin-down. (It is directly analogous to Schrödinger’s cat: cat=particle, awake=spin-up, asleep=spin-down.) Classically, the possible states are
“spin is up”
or
“spin is down”.
Quantum mechanics says that the state of the particle can be a superposition of both possible measurement outcomes. It’s not that we don’t know whether the spin is up or down; it’s that it’s really in a superposition of both possibilities, at least until we observe it. We can denote such a state like this:
(“spin is up” + “spin is down”).
While classical states are points in phase space, quantum states are “wave functions” that live in something called Hilbert space. Hilbert space is very big — as we will see, it has room for lots of stuff.
To describe measurements, we need to add an observer. It doesn’t need to be a “conscious” observer or anything else that might get Deepak Chopra excited; we just mean a macroscopic measuring apparatus. It could be a living person, but it could just as well be a video camera or even the air in a room. To avoid confusion we’ll just call it the “apparatus.”
In any formulation of quantum mechanics, the apparatus starts in a “ready” state, which is a way of saying “it hasn’t yet looked at the thing it’s going to observe” (i.e., the particle). More specifically, the apparatus is not entangled with the particle; their two states are independent of each other. So the quantum state of the particle+apparatus system starts out like this:
(“spin is up” + “spin is down” ; apparatus says “ready”) (1)
The particle is in a superposition, but the apparatus is not. According to the textbook view, when the apparatus observes the particle, the quantum state collapses onto one of two possibilities:
(“spin is up”; apparatus says “up”)
or
(“spin is down”; apparatus says “down”).
When and how such collapse actually occurs is a bit vague — a huge problem with the textbook approach — but let’s not dig into that right now.
But there is clearly another possibility. If the particle can be in a superposition of two states, then so can the apparatus. So nothing stops us from writing down a state of the form
(spin is up ; apparatus says “up”)
+ (spin is down ; apparatus says “down”). (2)
The plus sign here is crucial. This is not a state representing one alternative or the other, as in the textbook view; it’s a superposition of both possibilities. In this kind of state, the spin of the particle is entangled with the readout of the apparatus.
What would it be like to live in a world with the kind of quantum state we have written in (2)? It might seem a bit unrealistic at first glance; after all, when we observe real-world quantum systems it always feels like we see one outcome or the other. We never think that we ourselves are in a superposition of having achieved different measurement outcomes.
This is where the magic of decoherence comes in. (Everett himself actually had a clever argument that didn’t use decoherence explicitly, but we’ll take a more modern view.) I won’t go into the details here, but the basic idea isn’t too difficult. There are more things in the universe than our particle and the measuring apparatus; there is the rest of the Earth, and for that matter everything in outer space. That stuff — group it all together and call it the “environment” — has a quantum state also. We expect the apparatus to quickly become entangled with the environment, if only because photons and air molecules in the environment will keep bumping into the apparatus. As a result, even though a state of this form is in a superposition, the two different pieces (one with the particle spin-up, one with the particle spin-down) will never be able to interfere with each other. Interference (different parts of the wave function canceling each other out) demands a precise alignment of the quantum states, and once we lose information into the environment that becomes impossible. That’s decoherence.
Once our quantum superposition involves macroscopic systems with many degrees of freedom that become entangled with an even-larger environment, the different terms in that superposition proceed to evolve completely independently of each other. It is as if they have become distinct worlds — because they have. We wouldn’t think of our pre-measurement state (1) as describing two different worlds; it’s just one world, in which the particle is in a superposition. But (2) has two worlds in it. The difference is that we can imagine undoing the superposition in (1) by carefully manipulating the particle, but in (2) the difference between the two branches has diffused into the environment and is lost there forever.
All of this exposition is building up to the following point: in order to describe a quantum state that includes two non-interacting “worlds” as in (2), we didn’t have to add anything at all to our description of the universe, unlike the classical case. All of the ingredients were already there!
Our only assumption was that the apparatus obeys the rules of quantum mechanics just as much as the particle does, which seems to be an extremely mild assumption if we think quantum mechanics is the correct theory of reality. Given that, we know that the particle can be in “spin-up” or “spin-down” states, and we also know that the apparatus can be in “ready” or “measured spin-up” or “measured spin-down” states. And if that’s true, the quantum state has the built-in ability to describe superpositions of non-interacting worlds. Not only did we not need to add anything to make it possible, we had no choice in the matter. The potential for multiple worlds is always there in the quantum state, whether you like it or not.
The next question would be, do multiple-world superpositions of the form written in (2) ever actually come into being? And the answer again is: yes, automatically, without any additional assumptions. It’s just the ordinary evolution of a quantum system according to Schrödinger’s equation. Indeed, the fact that a state that looks like (1) evolves into a state that looks like (2) under Schrödinger’s equation is what we mean when we say “this apparatus measures whether the spin is up or down.”
The conclusion, therefore, is that multiple worlds automatically occur in quantum mechanics. They are an inevitable part of the formalism. The only remaining question is: what are you going to do about it? There are three popular strategies on the market: anger, denial, and acceptance.
The “anger” strategy says “I hate the idea of multiple worlds with such a white-hot passion that I will change the rules of quantum mechanics in order to avoid them.” And people do this! In the four options listed here, both dynamical-collapse theories and hidden-variable theories are straightforward alterations of the conventional picture of quantum mechanics. In dynamical collapse, we change the evolution equation, by adding some explicitly stochastic probability of collapse. In hidden variables, we keep the Schrödinger equation intact, but add new variables — hidden ones, which we know must be explicitly non-local. Of course there is currently zero empirical evidence for these rather ad hoc modifications of the formalism, but hey, you never know.
The “denial” strategy says “The idea of multiple worlds is so profoundly upsetting to me that I will deny the existence of reality in order to escape having to think about it.” Advocates of this approach don’t actually put it that way, but I’m being polemical rather than conciliatory in this particular post. And I don’t think it’s an unfair characterization. This is the quantum Bayesianism approach, or more generally “psi-epistemic” approaches. The idea is to simply deny that the quantum state represents anything about reality; it is merely a way of keeping track of the probability of future measurement outcomes. Is the particle spin-up, or spin-down, or both? Neither! There is no particle, there is no spoon, nor is there the state of the particle’s spin; there is only the probability of seeing the spin in different conditions once one performs a measurement. I advocate listening to David Albert’s take at our WSF panel.
The final strategy is acceptance. That is the Everettian approach. The formalism of quantum mechanics, in this view, consists of quantum states as described above and nothing more, which evolve according to the usual Schrödinger equation and nothing more. The formalism predicts that there are many worlds, so we choose to accept that. This means that the part of reality we experience is an indescribably thin slice of the entire picture, but so be it. Our job as scientists is to formulate the best possible description of the world as it is, not to force the world to bend to our pre-conceptions.
Such brave declarations aren’t enough on their own, of course. The fierce austerity of EQM is attractive, but we still need to verify that its predictions map on to our empirical data. This raises questions that live squarely at the physics/philosophy boundary. Why does the quantum state branch into certain kinds of worlds (e.g., ones where cats are awake or ones where cats are asleep) and not others (where cats are in superpositions of both)? Why are the probabilities that we actually observe given by the Born Rule, which states that the probability equals the wave function squared? In what sense are there probabilities at all, if the theory is completely deterministic?
These are the serious issues for EQM, as opposed to the silly one that “there are just too many universes!” The “why those states?” problem has essentially been solved by the notion of pointer states — quantum states split along lines that are macroscopically robust, which are ultimately delineated by the actual laws of physics (the particles/fields/interactions of the real world). The probability question is trickier, but also (I think) solvable. Decision theory is one attractive approach, and Chip Sebens and I are advocating self-locating uncertainty as a friendly alternative. That’s the subject of a paper we just wrote, which I plan to talk about in a separate post.
There are other silly objections to EQM, of course. The most popular is probably the complaint that it’s not falsifiable. That truly makes no sense. It’s trivial to falsify EQM — just do an experiment that violates the Schrödinger equation or the principle of superposition, which are the only things the theory assumes. Witness a dynamical collapse, or find a hidden variable. Of course we don’t see the other worlds directly, but — in case we haven’t yet driven home the point loudly enough — those other worlds are not added on to the theory. They come out automatically if you believe in quantum mechanics. If you have a physically distinguishable alternative, by all means suggest it — the experimenters would love to hear about it. (And true alternatives, like GRW and Bohmian mechanics, are indeed experimentally distinguishable.)
Sadly, most people who object to EQM do so for the silly reasons, not for the serious ones. But even given the real challenges of the preferred-basis issue and the probability issue, I think EQM is way ahead of any proposed alternative. It takes at face value the minimal conceptual apparatus necessary to account for the world we see, and by doing so it fits all the data we have ever collected. What more do you want from a theory than that?
Is it your view that the many-worlds interpretation has become more popular in, say, the last 15 years?
What do you think of the cosmological interpretation of Aguirre and Tegmark?
S0 my guess is that you would object to the interpretations here (I may be misunderstanding the piece completely)
http://www.wired.com/2014/06/the-new-quantum-reality/
But if I understand it right it’s basically a hidden variables interpretation.
Occam’s Razor makes me agree with the MWI. It exorcises the measurement problem better than other convoluted explanations.
I understand how dynamical collapse is (hypothetically) experimentally distinguishable from Many-Worlds, but I don’t understand how Bohmian mechanics is. Could you explain?
I’m also curious what you think of recent arguments based on the PBR theorem that local psi-epistemic models fail.
I would love to read your thoughts about the Bohmian view, and especially that Wired article. I don’t know what to think about it. As a fluid mechanics guy myself, it’s definitely interesting, but I have to believe there is a better reason that pilot waves aren’t more talked about than what the article implied. My guess? If these pilot waves can affect trajectories of particles (i.e., stuff), then wouldn’t we expect to be able to detect them directly somehow?
So is time quantized and quantumly indeterminant below some level?
Sean,
Since you’re being “polemical rather than conciliatory”, I hope you’ll let me raise one point… 🙂
I don’t see the pointer basis problem anywhere near being solved. AFAIK, the main argument in all proposed solutions (that I saw) is that the interactions are local in space, which provides one with a preferred basis (the eigenstates of the interaction Hamiltonian). IOW, the existence of the pointer basis is based on locality of interactions.
But interactions are local only until one quantizes gravity. As soon as you are allowed to construct a superposition of two spacetime manifolds (which is an essential feature of QG), locality of interactions goes out the window.
And once locality is gone, the pointer basis is also gone, and the measurement problem ressurects itself in its original form — there is no preferred way to split the wavefunction into branches.
The issue here is that most of the people who are researching this stuff do so in the non(general)relativistic approximation, i.e. they assume the existence of a flat Minkowski spacetime (or other fixed background), which implicitly gives them a well-defined notion of locality. They simply ignore quantum gravity issues.
So I’d say that the resolution of the pointer basis problem in EQM requires an additional postulate, much like in all other versions of QM. And the EQM folks just seem to be in denial of this problem, believing that they “solved” it, IMO.
Best, 🙂
Marko
Sean, is there any particular objection you have to the decoherent histories approach? This approach employs decoherence and the Copenhagen interpretation to provide a single logical framework for quantum and classical physics.
I like the Many-Worlds interpretation for its “economy” of formalism. I.e. You don’t need anything other than the raw, pragmatic equations of quantum mechanics. But decoherent histories seems to be a way to keep this economy of formalism without postulating an ensemble of deterministic realities.
I believe there are many silly interpretations in Quantum Theory, and agree there are many silly arguments for and against one version or another as Sean explains. What I have against EQM in particular is that I believe it is not in accord with Occam’s Razor (it may be the most complicated explanation) for what we observe in the quantum world. Still I applaud all attempt to logically justify any version of Quantum Theory.
Of the choices offered in the Quantum Smackdown, QBism seems like the simplest explanation to me, but simpler than this, IMO, would be a quantum theory involving local hidden variables. Although most think that local hidden variables are not possible based upon Bell’s logical argument, there are contrary arguments.
Today we have such hypothesis as dark matter, dark energy, gravitons, Higgs particles, quantum foam, virtual particles, etc. Any and all of these particulates/ fields or other aether-like entities, can be considered hidden variables within a background field. Any such particulate entities could effect interactions in the quantum world and IMO could enable a much simpler macro-world-like explanation of Quantum Mechanics compatible with classical physics.
Well done Sean. Simple fact, if quantum evolution is unitary and our models in science have more than mere instrumental value , like it or not, you’re stuck with many worlds. My prejudice is that , with regard to the Born rule , the proposal by Aguirre and Tegmark, the so called Cosmological interpretation offers some promise. I think you would call this branch counting. However, I am reading through the paper you wrote too. I look forward to reading your post on this, as well as to why MWs actually works. These posts are very much appreciated by me.
“The potential for multiple worlds is always there in the quantum state, whether you like it or not.”
That needs to be a on a (large) bumper sticker.
Consistent ( Decoherent) Histories is a totally instrumentalist interpretation , the way issues like quantum non local correlations in measurement records are viewed is cringe worthy in my opinion. However the actual mathematical formalism of CH is , again in my opinion, very productive in illuminated the quantum measurement process. I have often wondered why advocates of many worlds haven’t embraced the CH formalism. Rather than being centered on endless world splitting , we might better think of unitary evolution, together with the Decoherence process as producing a large number of consistent histories. We can even quantify these histories because in the CH mathematical formalism the total number of possible consistent histories is equal to the square of the Hilbert Space Dimension. We can further quantify the Hilbert Space Dimension via the Holographic principle. (t’Hooft dimensional reduction)
This raises an interesting issue. As proved by Dowker and Kent, the total number of consistent histories is far greater than the number of consistent histories which look like our classical world. Is this a failure of the consistency criteria or a fascinating fact about the product of the decoherence process? Gell-Mann and Hartle have argued that our sensory neurological capabilities evolved to only model reality in terms of predictive histories, which they argue are the quasi-classical histories we directly experience. Now if true, that’s really interesting.
I know this is a naive question, but: why is this a problem that has to be solved? Why can’t we deal with this the way we deal with lots of other strange things in physics, by saying that our physical intuitions don’t work well at scales very different from the ones they developed for, and leave it at that?
Put another away: You could say, “The formalism of QR says that macroscopic systems behave as if there were many worlds.” Or you could say, “The formalism of QR says that macroscopic systems behave as if there were many worlds — and there really are” How is the second an improvement over the first? What does the claim that a hypothesis is “true” add to the claim that it is predictively successful, aesthetically satisfying and productive of new insights?
“To describe measurements, we need to add an observer. It doesn’t need to be a “conscious” observer or anything else that might get Deepak Chopra excited; we just mean a macroscopic measuring apparatus. It could be a living person, but it could just as well be a video camera or even the air in a room. To avoid confusion we’ll just call it the “apparatus.”
I’ve never understood what this means in practice. Does this imply that “measurements” are taking places billions or trillions of times every second throughout the universe? And have been since the Big Bang? Is any interaction a measuring apparatus? I’m sure I’m missing something obvious. Maybe if I understood what would not be a measurement?
So, what happens to the law of conservation of mass-energy when another universe is spawned by peeking into the box?
A very nice description of the Many-worlds interpretation. I personally view Many-worlds interpretation as a candidate for reality, but I remain unconvinced that we’ve reached the point where we can move it from candidate to settled.
If we falsify the Schrodinger equation or superposition, we’ve falsified Many-worlds, but haven’t we also falsified every other interpretation? To consider Many-worlds falsifiable, don’t we need to be able to, at least in principle, uniquely falsify it?
Occam’s razor seems like a tough call on these interpretations. Is mathematical parsimony the same thing as ontological parsimony? I’m not sure of the answer, but dismissing the concern as silly seems unjustified.
I’m probably being dense, but there’s still one thing I don’t get about MW. I have never liked the Copenhagen interpretation because of its unjustified introduction of the concepts of “collapse” and “measurement”, without ever defining rigorously what a “measurement” is. How does MW solve this issue? The explanation here still contains words like “measurement” and “measuring apparatus” that is “prepared”, and so on. Is a proper understanding of decoherence required of the reader in order to understand that in MW these things are rigorously defined?
On a related note, is a “measurement” and the “creation” of two worlds in the MW sense a discrete event, or is it the case that the states drift apart little by little until they can no longer interfere? For the non-mathematician, does it make sense to think of decoherence as something that emerges from the sum of many interactions, much like pressure and temperature emerge from a gas of many particles, but are meaningless when discussing very few particles?
Pingback: Sean Carroll makes the case for the Many-worlds interpretation of quantum mechanics | SelfAwarePatterns
Sean,
Several remarks.
The first is that classical physics does indeed allow us to describe multiple worlds provided that we interpret classical probabilities according to something like David Lewis’s modal realism. When studying the evolution of classical probability distributions, all the states “are just there” in the formalism, so why not simply accept that they exist in reality, as one does in EQM?
My second remark is about axioms. All logical claims consist of premises, arguments that follow from those premises, and conclusions, and EQM is no different. Proponents often suggest that EQM doesn’t need as many axioms as the traditional interpretations. But the trouble with EQM is that although it seems at first like you don’t need very many axioms, the truth is that you do. Simply insisting that we don’t mess with the superposition rule isn’t enough. Quantum-information instrumentalism (say, QBism) doesn’t mess with superpositions either, and allows arbitrarily large systems to surperpose. Declaring that we must interpret the elements of a superpositions as physical parallel universes is therefore an affirmative, nontrivial axiom about the ontology of the theory, even if some people might regard it as an “obvious” axiom.
The pointer-variable argument also implicitly assumes axioms as well. We have to declare that something singles out a preferred basis (for the cat, this means that we need to single out the alive vs. dead basis, rather than, say, the alive+dead vs. alive-dead basis). You can keep adding additional systems and environments, but at some point you have to declare that once you’ve added enough, you can shout “stop!” and pick your preferred basis. And what is our criterion for picking that basis? That’s going to be another axiom! And if you pick locality or something like that for specifying your preferred-basis-selection postulate, you have to contend with the fact that locality may not be a fundamental feature of reality once we figure out quantum gravity, so if we do add locality as part of our axiom for picking the preferred basis, the EQM interpretation is now sensitive to features of quantum gravity that we don’t know yet.
Finally, are you assuming that there’s some big universal wave function that evolves unitarily? Given all we know about eternal inflation, is this a reliable assumption anymore? Even if you’re willing to accept it, it represents another axiom to add on.
The problem with EQM is that this process of adding axioms keeps going on (your “epistemic separability principle,” for example, is another axiom, and far from an obvious one!), and even then we still have to contend with the serious trouble of trying to make sense of the concept of probability starting from deterministic assumptions, a serious philosophical problem on par with the is-ought problem of Hume.
Dear Professor Carroll,
OK, I’m sure you’re not going to like this but seeing the state of the problem of QM meets GR, and the problem of time, I’ll put it out there anyway.
(People seem to say they want paradigm shifts, but don’t actually seem to like them at first sight).
I think that it makes sense in complicated matters to at least be sure our most basic assumptions are sound and logical. So…
The Many-Worlds formulation of QM, like any formulation has to, I assume, ultimately work with General Relativity, or some modification of it, such that the ‘suggested’ “problem of Time” is resolved.
Thus we might typically assume phenomena such as space-time, and retro-causality etc ultimately need to be accounted for and incorporated into any final resolution of GR and QM.
However, surely, GR, and the concept of space-time very much rests on Minkowski’s interpretation of SR, outlined in the famous quote
“The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality”
But if we look at “ON THE ELECTRODYNAMICS OF MOVING BODIES”, i.e the heart of Relativity, Section 1 says…
“[we must be…] quite clear as to what we understand by “time.”
We have to take into account that all our judgments in which time plays a part are always judgments of simultaneous events. If, for instance, I say, “That train arrives here at 7 o’clock,” I mean something like this: “The pointing of the small hand of my watch to 7 and the arrival of the train are simultaneous events.”
And the paper goes on from there… leading to SR and ultimately GR and the ‘Space-Time’ we assume QM happens in, etc
But surely all that is described in this key section of such an important paper, is the fact that aggregates of matter (be it a train on a track, or a motorised hand on a numbered dial) can exist, and be moving or stationary, and their speeds an/or locations can be compared.
Critically (and this is the bit you’re not going to like, but that may also be very important, imo) the paper simply ‘declares’ that the motion of the hand, smoothly rotating, in one direction, on a numbered dial, not only shows that ‘a hand can rotate’, but (apparently) also, that a thing called ‘time’ exists in some form, and is ’passing’ smoothly, in one direction.
Similarly by the word ‘simultaneous’, it is implied but not proven (to any degree at all here) that ‘time’, and ‘different times’ exist.
But surely the train, the ‘hand’, and anything else in the universe is always just ‘somewhere’ doing ‘something’. (though it may be doing this something at a dilated rate).
My point being if QM has to work with GR, and GR is built on assumptions made in and about SR, can anyone please actually show where in ‘ELECTRODYNAMICS’, or anywhere else in Einstein’s work, the existence of time, and/or past, or future is actually proven to any level? Rather than just assumed in, (with respect) a rather weak manner, but built on as if proven.
If no one can point to an actual proof of time in this context, then surely SR essentially just shows how, if moving at a significant velocity relative to an observer, the rate at which a moving oscillator… vibrates, is unexpectedly dilated.
And very specifically, not (imo) that a thing called time exists. And not that a past of future exist, And not that the rate at which a thing called ‘time’ flows between a past and future is dilated. And thus also not that the concept of space-time is valid.
If this is the case then surely we have no actual valid reason to suspect 4d ‘space time’ exists. Instead GR may need only describe how ‘3d’ warped space exists, and how velocity, gravity, and acceleration, can dilate rates of change, and warp and curve space (e.g. even back on itself)… but all just ‘now’ so to speak.
If my analysis is completely wrong, could someone here please cut/past a clip showing Einstein’s reasons/proof for assuming the ‘watch’ hand does not just rotate, but also relates to the passage of a thing called time. (or anyone else’s proof, rather than unchecked assumption).
i.e Minkowski’s quote clearly references “The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength”
So can someone please point to the experimental physics that Minkowski claims, proves a watch hand is not just a motorised hand rotating, but also actually shows the existence, and passage of ‘time’.
(I’m sure this sounds like a very naive request to yourself, but then it should likewise be very easy to do, my point being every expert, and many theories, seem to insist Einsteins Relativity proves space-time, and thus proves ‘time‘, but all I see at the start of ELECTRODYNAMICS, re time, is a assumption that because things move, time, and a past and future exist).
I know you’re a big fan of entropy, but without a proof of time, surely entropy is just the observable fact that the universe is expanding… and not a proof that a past or future exist, and thus also not a proof that time, exists or flows between these unproven ‘places’, with or without an ‘arrow‘.
Like I say, I assume you’re not going to like this post, but rather than just ignore it or delete it etc, I’d really appreciate it if you could at least actually post a link to the established proof that past/future/time exist.
Many thanks, Sincerely,
Matthew Marsden.
I have read recently about the bouncing oil-droplet experiment which may indicate that reality prefers pilot-wave theory, shouldn’t it be considered seriously now?!
Great article Sean.
I definitely tend to lean towards the MWI as well. I was wondering if anyone had seen the recent binge of great articles on a few other interpretations of QM:
Article on the Bohm Interpretation (which I’m also sympathetic with):
http://www.simonsfoundation.org/quanta/20140624-fluid-tests-hint-at-concrete-quantum-reality/
Sciam blog highlights objective collapse theory:
http://blogs.scientificamerican.com/critical-opalescence/2014/06/26/physicists-think-they-can-solve-the-mysteries-of-quantum-mechanics-cosmology-and-black-holes-in-one-go-guest-post/
Both of the above have the benefit of being realist (with respect to the wavefuction), but I don’t think the objective collapse theories indeterminism gets it as far as MWI or pilot wave theory, both of which are fully deterministic.
Any thoughts from Sean or anyone else?
Philosophically it is an interesting question whether multiple worlds are to be considered real and not just a mathematical construction. Does this place a restriction on proving there is no free will? Outcomes are deterministic (assumption), but no prediction is exact. When weighed across all possible outcomes, even a relatively simple system with only about 60 spins, becomes impossible to predict, which is functionally equivalent to not knowing the future, and therefore provides a proof that free will exists for anyone who cares enough about predicting the future, i.e., sentient beings.
Hi Bob,
What is it about the consistent histories description of correlation that you find cringe-worthy? In the CH interpretation, all correlations arise from local interactions, and do not imply any non-local interactions.
Do you have a link to the studies which show there are more consistent histories than consistent histories that look classical? I was under the impression that, because the probability of a history is derived from the projection operators used to construct the history, all non-classical histories would have zero probability.
Here’s the thing: If you assume that QM is correct, then it may be true that the MWI is the “best/simplest” explanation.
But you have to assume that we really understand what is going on in QM, and I think it’s clear we do not. It seems much more likely from my perspective that we are missing something fundamental.
All this talk of Many Worlds, while it could be true, are ideas gone too far, assuming too much, and will be just plain unnecessary when we finally do understand what’s actually going on in QM.