General relativity is a rich theory that makes a wide variety of experimental predictions. It’s been tested many ways, and always seems to pass with flying colors. But there’s always the possibility that a different test in a new regime will reveal some anomalous behavior, which would open the door to a revolution in our understanding of gravity. (I didn’t say it was a likely possibility, but you don’t know until you try.)
Not every experiment tests different things; sometimes one set of observations is done with a novel technique, but is actually just re-examining a physical regime that has already been well-explored. So it’s interesting to have a handle on what regimes we have already tested. For GR, that’s not such an easy question; it’s difficult to compare tests like gravitational redshift, the binary pulsar, and Big Bang nucleosynthesis.
So it’s good to see a new paper that at least takes a stab at putting it all together:
Linking Tests of Gravity On All Scales: from the Strong-Field Regime to Cosmology
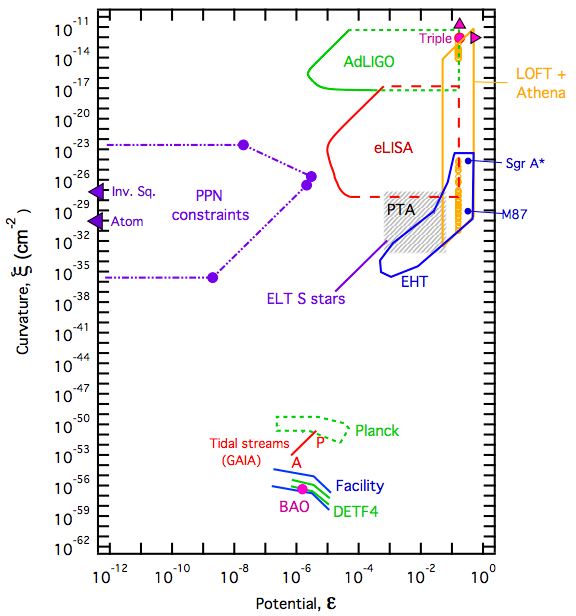
Tessa Baker, Dimitrios Psaltis, Constantinos SkordisThe current effort to test General Relativity employs multiple disparate formalisms for different observables, obscuring the relations between laboratory, astrophysical and cosmological constraints. To remedy this situation, we develop a parameter space for comparing tests of gravity on all scales in the universe. In particular, we present new methods for linking cosmological large-scale structure, the Cosmic Microwave Background and gravitational waves with classic PPN tests of gravity. Diagrams of this gravitational parameter space reveal a noticeable untested regime. The untested window, which separates small-scale systems from the troubled cosmological regime, could potentially hide the onset of corrections to General Relativity.
The idea is to find a simple way of characterizing different tests of GR so that they can be directly compared. This will always be something of an art as well as a science — the metric tensor has ten independent parameters (six of which are physical, given four coordinates we can choose), and there are a lot of ways they can combine together, so there’s little hope of a parameterization that is both easy to grasp and covers all bases.
Still, you can make some reasonable assumptions and see whether you make progress. Baker et al. have defined two parameters: the “Potential” ε, which roughly tells you how deep the gravitational well is, and the “Curvature” ξ, which tells you how strongly the field is changing through space. Again — these are reasonable things to look at, but not really comprehensive. Nevertheless, you can make a nice plot that shows where different experimental constraints lie in your new parameter space.
The nice thing is that there’s a lot of parameter space that is unexplored! You can think of this plot as a finding chart for experimenters who want to dream up new ways to test our best understanding of gravity in new regimes.
One caveat: it would be extremely surprising indeed if gravity didn’t conform to GR in these regimes. The philosophy of effective field theory gives us a very definite expectation for where our theories should break down: on length scales shorter than where we have tested the theory. It would be weird, although certainly not impossible, for a theory of gravity to work with exquisite precision in our Solar System, but break down on the scales of galaxies or cosmology. It’s not impossible, but that fact should weigh heavily in one’s personal Bayesian priors for finding new physics in this kind of regime. Just another way that Nature makes life challenging for we poor human physicists.
Hi Dr. Carroll,
This is another great post about something I’ve been curious about. It’s immensely valuable for the future of science to develop techniques that will get us closer to identifying areas that need further testing — so we can solidiy or evolve our understanding of gravity (or any other domain).
Thank you for your blog, lectures, YouTube videos, Great Courses series, and books! I’m a big fan and I’ve learned so much from you over the past few years. Please keep it up!
Gentleness and respect,
—Russell from russellandpascal.com
Has the speed of light ever been shown to be changed by a gravitational body through experiment? Do different planets used for measuring the speed of light show different speeds? Do experiments that measure the speed of light at different elevations show different values?
It seems like it has become fairly common for people on the net to think that the speed of light can differ under a gravitational influence. I have been fairly certain that this is not the case for some time. I really don’t know of any equations that make up for this alteration of this constant of nature… Although, I thought Special and General Relativity alike was formulated to change other values in order to keep this constant the same. By definition wouldn’t a constant then be unchanging in all respects?
John Barrett:
Speed of light is always the same locally, but apparent speed of light can be anything. A photon (or a graviton, if one discovered) in vacuum whizzes by you at the speed of light, no matter what. But it can appear to take longer when bending around a star, or even to be completely still on the event horizon of a black hole, all because you are not right there to “see” it go by. There is no paradox or contradiction. It’s just that General Relativity requires a completely different intuition, best developed through studying the underlying math.
Hi Dr. Carroll,
Thank you for your interesting point of view. I am busy with your course on the Arrow of Time and really enjoy your delivery of the material. Regarding the testing of GR in different ways I am intrigued as to what new findings will eventually surface. As a science fiction author I am always trying to improve my understanding of relativity and gravity in the hope that one day I will be able to write more authentic detail about how a spacecraft will be able to cancel gravity.
Regarding John Barrett’s post about the speed of light being the great constant, I was interested to find an article about the speed of light slowing down (by Barry Setterfield; my namesake but no relation). Check it out and tell me what you think – I would be interested to know.
Sean, just wanted to point out that not addressed in the paper (which is only concerned with classical, not quantum effects) is semi-classical GR, or quantum fields on a fixed background, from which several important effects, such as Hawking and Unruh radiation are derived. Despite being a weak-field, low-speed approximation, it has been experimentally shown to likely be incompatible with any known interpretation of Quantum Mechanics, be it objective collapse or many worlds. On the graph you quoted this would correspond to a diagonal line from the top right (stellar black holes) down to the middle-left (conditions on Earth).
Colin:
Barry Setterfield of Genesis Science Research is, unfortunately, a religion-motivated incompetent amateur, as is evident from his writings, and so is best ignored.
Re your SF story, some nearly-believable ways to overcome gravity, if not to cancel it, are the Alcubierre drive, Eagleworks Q-thruster, and any contraption using “exotic matter”.
John Barrett: Yes, the speed of light is observed to be different if the observer is in a different gravitational environment than the light. One experimental measurement of this is the Shapiro delay (http://en.wikipedia.org/wiki/Shapiro_delay). The time for a radar pulse to travel from earth to Venus and back is longer when the sun is near the path compared to when the sun is not near the path (and therefore the observed speed of light is slower). The increased time is not just due to the increased length of the slightly bent path. In fact the bending of the light can be calculated from the part of the wave front away from the sun going a little faster than the part of the front near the sun … just like is done for the bending of light at the interface between materials with different indices of refraction in optics. However, if we were in free fall near the path of the radar photon (instead of at the earth’s position in the sun’s gravitational potential), we would measure the standard speed c= 2.99792458 E+8 m/sec using the same standard rod and clock we had carried from earth after doing the previous measurement.
As a result of special relativity, we are used to hearing “the speed of light is a constant in all reference frames”. The statement is actually “the speed of light is constant in all frames related by a Lorentz transformation”. Lorentz transformations include spatial rotations and boosts (which are space-time parallel-piped strains) which leave invariant the (1,1,1,-1) diagonal metric. However, this metric is not left invariant by moving to a different gravitational potential (space-time squash strains) or moving to the region of a gravitational wave (two polarizations: space-space squash and space-space parallel-piped strains). Hence, the speed of light is not invariant when viewed from a different gravitational frame.
A more recent test of this relative speed of light logic may well be LIGO. In one set of coordinates (assumed to be the observer frame outside the region of the gravitational wave) GR predicts the gravitational wave will move the mirrors on one arm together and the mirrors of the perpendicular arm apart. The normal argument then assumes the speed of light is invariant, and therefore the laser wave front will arrive back to the splitter later along the lengthened path than along the shortened path. Thus the interference pattern will change, and the gravitational wave detected. Unfortunately, the speed of light seen by the external observer may not be the same along the two paths … being faster along the lengthened arm and slower along the shorted arm, thereby leaving a Michelson Interferometer’s interference pattern unchanged by a gravitational wave…we shall soon know.
Surely a hundred years after Einstein came up with GR, everybody knows how gravity works? It’s like this. A concentration of energy “conditions” the surrounding space altering its properties such that “a curvature of rays of light can only occur when the speed of light varies with position”. You can find plenty of examples Einstein saying this online. And you can find more recent examples such as the Shapiro delay or on Baez or on Ned Wright’s website. Light doesn’t curve because spacetime is curved. That confuses cause and effect and the map with the territory. You will not find Einstein saying that. It curves because space is inhomogeneous, like a car veers when it encounters mud at the side of the road.
Edit: well said Gary. Most people don’t appreciate that LIGO is an interferometer or that Einstein reintroduced an aether when he was doing GR.
All: the locally measured speed of light is only constant because we use the local motion of light to define our metre and our second. Which we then use to measure the local motion of light. See http://arxiv.org/abs/0705.4507 where Magueijo and Moffat referred to the tautology. The “coordinate” speed of light is not constant.
John D,
I would like for you to listen, and listen carefully. Please just shut up and shove your nonsense up your a$$.
David: follow the links. Einstein and Shapiro and Baez and Koks and Wright and Magueijo and Moffat aren’t talking nonsense.
I guess you don’t know how to follow simple instructions.
By the way, did it ever occur to you that perhaps Magueijo and Moffat are crackpots? Or do you believe everything they say?
Please don’t call people crackpots in the comment section. (Only I’m allowed to do that.)
Thanks Shmi,
Having read some of Barry Setterfield’s work I do know about his religious inclinations and how he uses his theory to support a sort of youngearth creationism. I have also read about Miguel Alcubierre’s drive that will allow FTL travel but Eaglework’s Q-thruster is new to me, so I will check it out.
Sean said:
Sean, I’d be very interested to hear your arguments. The infrared can certainly be modified in some way—the most straightforward example is if the theory admits massive gravitons, but with an inverse mass corresponding to galactic length scales. Or any of the other screening type mechanisms (e.g. Vainshtein). I know that most of the models end up looking quite ugly, but that’s not really an argument against generality. Care to comment?
Wow, lots of hate/downvotes/name calling. David, I want to give you the benefit of the doubt and assume you’re being sarcastic, but remember Poe’s law—online you’ll be interpreted as serious even if you’re kidding.
For those who think I’m spouting nonsense—please read some review articles first, and once you understand Vainshtein, chameleon, Galileon, and other screening mechanisms, come back and participate in serious discussions in IR corrections to GR.
Leo, many things are possible, I was just commenting on likelihood. The fact that the models are quite ugly isn’t just an accident; it’s a reflection of the fact that mass scales corresponding to astrophysically-interesting length scales are not at all what you would expect in an effective field theory. But again, I’m in favor of doing the tests.
Sean, is it a naturalness argument—that the natural UV cutoff scale is the Planck scale? That’s a totally valid argument in the UV. What is the equivalent argument for the IR cutoff? I don’t know what physics would be sensitive to such an IR cutoff besides gravity (I guess E&M is also long-ranged, so there could be some sensitivity to there as well).
It’s an effective field theory argument. There just aren’t that many terms you can write down in a Lorentz-invariant 4D effective theory, and generally you expect quantum corrections to drive mass scales up to the UV cutoff. (I’m not sure what IR cutoff you’re referring to.) Of course you can play all sorts of games with symmetries, branes, Lorentz violation, etc. To me it seems pretty contrived, but judgments will differ.
I’ve been troubled by a related, but a different, more fundamental, aspect of relativity testing—that of c being a universal constant.
In Einstein’s special relativity writings it is clear that he regarded the independence of the SL of the relative motion between source and observer as a postulate, an assumption that cannot be proved/falsified in isolation but that the truth of which emerges from the consistency and empirical success of the theory as a whole. (The difficulty lies in the impossibility of a one-way SL measurment in the absence of an absolute clocks pre-synchronization.)
But it’s one thing to say that the SL is independent of such motions, it’s another thing to say that the value of the SL is constant throughout a particular spacetime region and in a particular test/observation setup, and it’s still another thing to postulate that c is a universal constant, so that we can drop it from our cosmological equations by normalizing it to 1. Since all our empirical evidence about the value of c is necessarily local—of solar system extent at most—and since all our cosmological theories are open-ended in this respect (proof/falsification of this postulate involving such theories is necessarily circular,) how can we justify it? How can we be confident that the SL was c during the big bang? And if we can’t, isn’t it a better idea to keep c in the equations, at least as a reminder that theoretical things might still happen to it? Sean, would you please educate us on this?
(Proper disclosure: I am a science secularist at heart—I don’t seek to support a belief in recent creation.)
The speed of light changing in a gravitational field seems rather intriguing. I believe I have gotten to a point where I understand why spacetime would dilate in The Special Theory of Relativity, but when I try to apply that understanding to the General Theory it doesn’t seem to work out.
Light has to travel at an angle from a moving body, so it travels at a longer distance. Both observers have to measure the photon traveling at the same speed, so they have different measurements of units of spacetime that makes them do just that. If you consider the equivalence of acceleration and the force of gravity, an accelerating body will have a photon move in a curved path, and then the speed of the photon could be different as well. If the photon traveling the curved path can just be measured to travel at a different speed, then why should each observer even measure their units of spacetime to be different? They could essentially just say that they both measured it to be a different speed, and their clocks and rulers could stay the same. If it is true that the speed of light can change in a gravitational field, then it seems like the reason behind gravitational spacetime dilation would have to be for some other completely different type of reason.
Then would it also be true that an observer in an accelerating frame would not measure the same gauge symmetries? It would make it seem like one could continue accelerating fast enough to where they could catch up to a photon, instead of always measuring it to be the same speed no matter how fast they traveled.
The “handle on…regimes we have already tested,” curiously, contains a large gap across the board, i.e., across the whole range from Planck scale to the cosmos.
What has never been tested is the “regime” near the center of any body of gravitating matter. Specifically, GR predicts (as per the Schwarzschild interior solution) that the rate of a clock at the center of a given gravitating body is a minimum.
The more well known counterpart for this consequence of GR is the Newtonian prediction that a test object dropped into a hole through a larger body of matter is supposed to oscillate between the extremities. Neither of these predictions have ever been tested.
Physicists think they know the result of the experiment, but, as Carroll admits, we cannot “know until [we] try” actually doing the experiment. (“Testing our Theories is not a Matter of Envy.”)
Ironically, Galileo proposed the experiment over 380 years ago. Even if it does not lead to “a revolution in our understanding of gravity,” surely it is in the interest of science to fill the gap in our knowledge of gravity by performing the experiment proposed by the Father of Modern Science so long ago.
Additional arguments for doing the experiment can be found in the link below and references therein.
http://gravitationlab.com/Grav%20Lab%20Links/Gravity-Experiment-in-Waiting.pdf
“It would be weird, although certainly not impossible, for a theory of gravity to work with exquisite precision in our Solar System, but break down on the scales of galaxies or cosmology.”
I’m not sure I get this.
My understanding is that dark energy is a wrinkle that was uncovered only recently due to observations on the cosmological scale. Do you consider that not applicable because it’s now been incorporated into GR, or that it’s independent of GR, or something else I’m not considering.
Dark energy is just an energy source for general relativity, not a modification of the theory. Of course there are modifications of the theory (some of them are my fault), but none as simple and straightforward as just sticking in vacuum energy and keeping GR unchanged.
@John Barrett re “The speed of light changing in a gravitational field seems rather intriguing”. A gravitational field is a region of space where the speed of light is not constant. Einstein said this time and time again, and you can now look it up yourself in the Einstein papers:
“As a simple geometric consideration shows, the curvature of light rays occurs only in spaces where the speed of light is spatially variable”.
Einstein was not a crackpot.
@JohnD
I never said Einstein was a crackpot. I didn’t say he was wrong either. I was asking why that was true. Although, I do think he miss-assigned the time variables in the light clock example, and that is why it never really worked out right.
The observer at rest would measure the light to travel at an angle, so they would use their time to measure it travel that greater distance. Then the observer in constant motion would measure the light to travel straight up and down, so they would use their own time for it to travel that distance. With this correction, you can use use Pythagorean Theorem for the equation of each distance; vt, ct, and ct’.
(vt)^2 + (ct’)^2 = (ct)^2
v^2 t^2 + c^2 t’^2 = c^2 t^2 Distribute the square.
c^2 t’^2 = c^2 t^2 – v^2 t^2 Subtract both sides by v^2 t^2.
c^2 t’^2 = c^2 t^2 (1 – v^2 / c^2) Factor out c^2 t^2 from the right side.
t’^2 = t^2 (1 – v^2 / c^2) Divide both sides by c^2.
t’ = t sqrt(1 – v^2/c^2) Take the square root of both sides.
Then in this case t’ = tau, and then it would be equivalent to the equation for the proper time. That would make sense if t’ was originally the time that the observer in constant motion was using.