You know it’s a good day when there are refereed articles in Science about poker. (Enthusiasm slightly dampened by the article being behind a paywall, but some details here.)
Poker, of course, is a game of incomplete information. You don’t know your opponent’s cards, they don’t know yours. Part of your goal should be to keep it that way: you don’t want to give away information that would let your opponent figure out what you have.
As a result, the best way to play poker (against a competent opponent) is to use a mixed strategy: in any given situation, you want to have different probabilities for taking various actions, rather than a deterministic assignment of the best thing to do. If, for example, you always raise with certain starting hands, and always call with others, an attentive player will figure that out, and thereby gain a great deal of information about your hand. It’s much better to sometimes play weak hands as if they are strong (bluffing) and strong hands as if they are weak (slow-playing). The question is: how often should you be doing that?
Now researchers at a University of Alberta group that studies computerized poker has offered and “essentially” perfect strategy for a very simple form of poker: Heads-Up Limit Hold’em. In Hold’em, each player has two “hole” cards face down, and there are five “board” cards face-up in the middle of the table; your hand is the best five-card combination you can form from your hole cards and the board. “Heads-up” means that only two players are playing (much simpler than a multi-player game), and “limit” means that there is any bet comes in a single pre-specified amount (much simpler than “no-limit,” where you can bet anything from a fixed minimum up to the size of your stack or your opponent’s, whichever is smaller).
A simple game, but not very simple. Bets occur after each player gets their hole cards, and again after three cards (the “flop”) are put on the board, again after a fourth card (the turn), and finally after the last board card (the river) is revealed. If one player bets, the other can raise, and then the initial better can re-raise, up to a number of bets (typically four) that “caps” the betting.
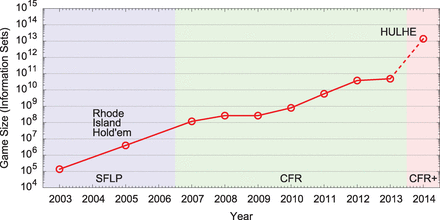
So a finite number of things can possibly happen, which makes the game amenable to computer analysis. But it’s still a large number. There are about 3×1017 “states” that one can reach in the game, where a “state” is defined by a certain number of bets having been made as well as the configuration of cards that have already been dealt. Not easy to analyze! Fortunately (or not), as a player with incomplete information you won’t be able to distinguish between all of those states — i.e. you don’t know your opponent’s hole cards. So it turns out that there are about 3×1014 distinct “decision points” from which a player might end up having to act.
So all you need to do is: for each of those 300 trillion possibilities, assign the best possible mixed strategy — your probability to bet/check if there hasn’t already been a bet, fold/call/raise if there has — and act accordingly. Hey, nobody ever said being a professional poker player would be easy. (As you might know, human beings are very bad at randomness, so many professionals use the second hand on a wristwatch to generate pseudo-random numbers and guide their actions.)
Nobody is going to do that, of course. So there might be a worry that advances like this will render human beings superfluous at playing poker. It’s not a realistic worry quite yet; despite it’s apparent complexity, Heads-up Limit is a sufficiently simple game that it’s almost never played by real people. Heads-up No-Limit, and multiplayer versions of both limit and no-limit, are played quite frequently; but they’re also much harder games to solve.
Which shouldn’t be taken as disparagement of the amazing things the Alberta group has achieved. To put it in context, they provide a plot of the sizes of imperfect-information games that have previously been essentially solved. Before this work, the most complicated solved game had less than 1011 decision points, whereas Heads-Up Limit Hold’em has over 1013 (after accounting for some symmetries in game configurations, which I presume means cards of equal value but different suits, etc.).
An impressive leap forward, relying on a technique known as “counterfactual regret minimization.” Essentially, the computer acts randomly at first, but keeps track of how much it regrets making a decision when things go badly, and adjusts its mixed strategy appropriately. Eventually an equilibrium is reached in which regrets are minimized. (If only we were allowed to live our lives this way…)
And, despite the simplicity of the game, you can certainly learn something from the strategy that the computer has worked out. Here is a plot with suggested actions for a couple of early decisions: on the left, what the dealer (who acts first) should do on their opening move, depending on what their hole cards are; on the right, what the other player should do if the dealer chose to raise. Red is fold, blue is call, and green is raise. (The dealer can fold as a first move, since the other player is forced to make a “blind” bet to start the action.)
Note that there is no blue in the left diagram. That means that the dealer should never simply call the blind bet without raising — a move known in the trade as “limping.” That fits well with received poker wisdom, which generally looks down on limping as an overly tentative and ultimately counter-productive strategy. Of course, no-limit is a different game, and one might still imagine a place for limping with a strong hand, since you can hope to get raised and then come over the top with a huge bet. But it’s food for thought for poker experts. (Also, note the lack of red in the right diagram — folding to a single bet is a bad idea with all but the worst hole cards. Hmm…)
As I said, this doesn’t affect real players in casinos very much, or at least not yet. Online poker is a different table of fish, of course. In the US, online poker is essentially dead, having been squelched by the federal government on what’s known in the community as Black Friday. But before that happened, there was already serious worry about online “bots” that could play many hands and beat all but the best human players. And the curve showing the growth in complexity of solved games is pretty impressive; it’s not impossible to imagine that No-Limit will be “essentially solved” in the foreseeable future.
Fortunately, like chess, knowing that there are computers better than you at poker doesn’t take away the pleasure of playing with ordinary human opponents. And if they tend to limp a lot, your pleasure might be even higher.

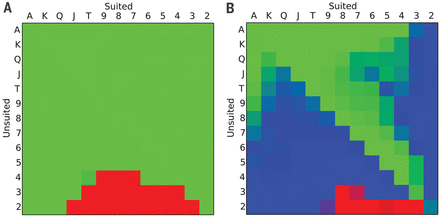
Looks like there’s actually one pixel (10-4 unsuited) where you should limp on a very rare occasion. Which seems odd, since your opponent could eventually figure out that’s the only time you limp…
I also like that if you’re 2nd to act with a pair of two’s it’s the only time you get to mix up all three options.
@Sean
as you are part of a university, you should be able to access the study through them (unless they don’t have membership to Science Mag, which would be weird considering…)
Here is the editors summary:
I’ll see your program and raise you mine
One of the fundamental differences between playing chess and two-handed poker is that the chessboard and the pieces on it are visible throughout the entire game, but an opponent’s cards in poker are private. This informational deficit increases the complexity and the uncertainty in calculating the best course of action—to raise, to fold, or to call. Bowling et al. now report that they have developed a computer program that can do just that for the heads-up variant of poker known as Limit Texas Hold ’em (see the Perspective by Sandholm).
(Science MAgazine – http://www.sciencemag.org/content/347/6218/145.full )
@Ian Paul Freeley,
From the paper,
So when Sean says you should never limp, he is only 99.94% correct. (This is, of course, unforgivable error.)
This is an interesting accomplishment. It appears to be another sector of human intelligence that won’t compete with AI, probabilistic problem solving. Imagine an AI sizing up a situation, synthesizing the ‘rules’, then using game theoretic reasoning algorithms to quickly determine the optimal strategy. Not ready today, but once we have more advanced processing it will be there. The only way we keep up is if we embed that technology into our brains. Borg, here we come.
Truck Captain Stumpy,
I suspect
is more of an ideological statement. A regret that most of us won’t be able to access the article, not that Sean himself can’t.
It is worth mentioning perhaps that the restriction to 2-players is important. It not only cuts down the number of possible states enormously, which helps in the computer calculations, in the 3-player game there simply will not exist a strategy that guarantees that you do not lose on average no matter how your opponents play.
I’m a bit confused here. As I understand it, to solve a game is to prove the game’s outcome from the initial position given perfect play (or to provide an algorithm capable of capturing at least a draw if not a win against all possible opponent move-sets). So when they say that they’ve “essentially” solved Poker (2-person Limit Hold ‘Em), they mean only that they have not in fact solved Poker in either the proof-theoretic or algorithmic sense. Rather, they have provided an algorithm sufficiently complex to win against most if not all actual poker players (assuming no actual poker player in fact plays poker perfectly).
Unlike say chess or checkers, it’s not clear to me what exactly it would mean to “play poker perfectly”, at least in a way that preserves the notion of “perfect play” across games (probabilistically vs. deterministically optimal) considered solved, partially solved, or unsolved but in principle solvable. Assuming it is on the solvable side, would its solution be sufficiently computationally complex to preclude any existing computer from carrying it out, forcing us to be content with computing some poor algorithmic stand-in nevertheless for all practical purposes sufficient to beat almost any human poker player?
“Counterfactual regret minimization…” sounds very human. The matchbox computer for learning and playing tictactoe many years ago had both regret minimization and satisfaction maximization built in. Of course it did not require any couldn’t-give-a-damn randomization. However, the important point about AI in such forms is that it bears little resemblance to human thought. Instead of playing out sufficiently vast numbers of scenarios both the chess grandmaster and the poker tyro rely on intuitive perceptions or predictions of pattern, as do theoretical physicists and poets.
If I knew I were facing this computer, then I could feasibly predict what probabilities it would act with. Given this knowledge, is it possible to compose another AI that uses different tactics which may not be generally optimal, but work for beating this one?
E.g., such that this AI beats a “typical” player, a “typical” player beats my “new AI” (since my new AI is designed only to beat this AI), and my AI beats this AI?
In other words: is it demonstrated (either does this optimization sufficiently demonstrate, by reaching equilibrium, or is there a proof elsewhere) that there is, necessarily, a “best strategy?” Or is this merely a “strategy which works against the most strategies?”
Magnema,
The definition of an optimal strategy is such that any strategy which deviates from it performs the same or worse (there may be many optimal strategies but none are “better” than any others). So your supposition that you could design an AI that could “beat” this one is flawed.
Put another way, when you play an optimal strategy you can tell your opponent exactly what you will do and he cannot do better than break even against you. This is easier to think about in much simpler games than poker.
Yes the claim from the university of alberta is that their strategy is the “best” strategy by virtue of brute force running out all possible scenarios (something that was previously too large to handle computationally).
Hello, Sean. I have a question regarding cosmology. I’ve come across some articles on the Internet written about cosmology in which the authors attempt to cast serious doubt on cosmology’s scientific rigour. In particular, people like to pull quotes from actual cosmologists in which the cosmologist himself says that cosmology is not a science. For example, the quote
“Cosmology may look like a science, but it isn’t a science… A basic tenet of science is that you can do repeatable experiments, and you can’t do that in cosmology” -James Gunn, Princeton University
is used often in creationist articles. Assuming that such quotes are real and not just gross distortions of the scientist’s actual words, my question is this: What do these cosmologists actually mean when they say that cosmology is not a science? Is it just a poor choice of wording? Because I’m personally well-convinced that cosmology is just as rigorous a science as any other branch of physics.
The strategy makes a lot of sense for heads up play. It takes going a really aggressive strategy to win more often than not in heads up. I am sure, with more players, a less aggressive strategy would have to be used to be successful. It seems like it would just want to pick up all the blind bets you possibly could by making the other player fold to the first bet. That would be the winning strategy. I don’t think that is anything new. Although, it would be a lot more difficult to pull off with more players that could possibly have much better starting hands. You wouldn’t be able to pick up the blinds as much.
It would be a lot more interesting how cards should be played with a full table. You couldn’t use the this same strategy for very long on a full table before you ended up losing all your chips! If the other player figured out you just raise mostly anything, they could call your bet with about everything you would consider to raise with, and if they started doing that it would be really difficult to know if they where bluffing in the following bets. Then they could just start picking up your raises anytime nothing connected for you. That would be a lot more chips than picking up the blinds.
Ian Paul Freeley: Regarding 10-4 unsuited, I infer from trivialknot’s reply that there are additional hole card combos for which the strategy specifies nonzero limp probability. (That said, respect for your impressive observational powers:-)
Chris: Kind of a nit but I believe I heard in a radio interview w/ one of the authors that their strategy is very slightly suboptimal (so slightly that the departure from optimality would only be noticeable after an astronomical number of hands).
arch1: Ian was referring to the opening bet only, whereas trivalknot’s quote refers to percentages across all possible scenarios of the entire game.
I do agree with Ian that it is rather odd. Knowing the other player has 10-4 unsuited could tell you whether or not to fold in many (most?) cases. Although possibly, since you don’t know the suits your opponent holds, she might be able to gain a slight edge by mixing it up, as there will be cases later in the hand where she may or may not have a flush (you will only know that there is a 50/50 chance). If that is a factor, I wonder more why other unsuited combinations don’t offer this exploit (with the further advantage that limping on the opening bet would not tip off your hole cards).
(Just to be pedantic, I know that it’s really less than 50/50 because 4 cards of the suit with the possible flush are already visible on the table. And of course you could have a flush yourself, so it’s just a question of whose flush is ranked higher…It gets complicated.)
Re: “trivalknot’s quote refers to percentages across all possible scenarios of the entire game”-
Thanks Richard. Is that clarification based on your looking at the paper itself? (I’m just checking, because I don’t see how one can conclude this based only on the quote).
Assuming that 10-4 unsuited is in fact the only opening-bet combination with a nonzero limp probability, I agree w/ you and Ian that its optimality is counterintuitive. That said, I cannot come up w/ an argument that rules this out (or even an argument that rules out a more extreme counterfactual scenario in which it could be optimal to limp sometimes even if this would require *turning up* one’s hole cards).
arch1, no, I haven’t gone behind the paywall to see the paper. But the quote was: “The strategy limps just 0.06% of the time and with no hand more than 0.5%.” It refers to “the strategy”, not “the opening bet”. Without that restriction I have to assume the entire game strategy is referred to. It would be hard to read the quote otherwise.
The diagram posted by Sean seems to indicate a deterministic strategy for every opening move except the one Ian noticed, unless there are even more subtle shadings present, that the eye can’t detect. If that reading is correct, then it would be hard to reconcile the quote with it while assuming the quote refers only to the opening.
Thanks Richard. I just noticed Sean’s 2nd URL above. A paragraph there may resolve this. It begins:
“Human players have disagreed about whether it may be desirable to “limp” (i.e., call as the very first action rather than raise) with certain hands. Conventional wisdom is that limping forgoes the opportunity to provoke an immediate fold by the opponent, and so raising is preferred. Our solution emphatically agrees (see the absence of blue in Fig. 4A). The strategy limps just 0.06% of the time and with no hand more than 0.5% ”
My best guess now is that the cited percentages do refer only to the initial decision, and that therefore (after a little math) it seems that at least a dozen or so of the hole-card combos must actually have nonzero limp probabilities. And that these escaped detection because all but one of relevant regions of chart 4A are visually identical to a pure fold or raise, even to Ian’s eagle eyes. Take a look and see if you agree.
arch1: Ah yes, given the definition of limp (a term I was not previously familiar with) that makes sense now.
Cepheus is not unbeatable, as I have already beaten it twice out of five 100-hand matches. It may beat most on-line challengers because the web interface is horrible and that beats down a human’s enthusiasm. Worse, the queue to play is 50 users long, but only two can play at once. It used to be 4 players, but I noticed the server kept crashing and you would get summarily tossed out of your match. So, you ended up waiting as long as two hours to get into a match and then might not get to finish it. There is also no indication of where you are in the queue, so you can easily get distracted and miss your 1-minute window to start playing, hours after you have finally gotten into the queue. It might help to pass the time, if you could see how the current players were doing. But no, there is very little action to watch. Still, if you can hang in there, it is not a perfect poker player, and you can learn how to beat it fairly rapidly. Cepheus still has to get cards to win, and that remains a 50-50 proposition. Don’t be intimidated by its betting strategy. Often, it doesn’t have good cards, but keeps betting into them. You can bluff it and slow play it effectively, lose small and win big, just like playing a person.
In the end I’d rather be lucky than good. This all works if you play “unlimited number of hands”. But in any small number situation luck will override all else. I won more money playing blackjack completely drunk then I did counting cards.