Thanksgiving

This year we give thanks for a simple but profound principle of statistical mechanics that extends the famous Second Law of Thermodynamics: the Jarzynski Equality. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, the Fourier Transform, Riemannian Geometry, and the speed of light.)

The Second Law says that entropy increases in closed systems. But really it says that entropy usually increases; thermodynamics is the limit of statistical mechanics, and in the real world there can be rare but inevitable fluctuations around the typical behavior. The Jarzynski Equality is a way of quantifying such fluctuations, which is increasingly important in the modern world of nanoscale science and biophysics.

Our story begins, as so many thermodynamic tales tend to do, with manipulating a piston containing a certain amount of gas. The gas is of course made of a number of jiggling particles (atoms and molecules). All of those jiggling particles contain energy, and we call the total amount of that energy the internal energy U of the gas. Let’s imagine the whole thing is embedded in an environment (a “heat bath”) at temperature T. That means that the gas inside the piston starts at temperature T, and after we manipulate it a bit and let it settle down, it will relax back to T by exchanging heat with the environment as necessary.

Finally, let’s divide the internal energy into “useful energy” and “useless energy.” The useful energy, known to the cognoscenti as the (Helmholtz) free energy and denoted by F, is the amount of energy potentially available to do useful work. For example, the pressure in our piston may be quite high, and we could release it to push a lever or something. But there is also useless energy, which is just the entropy S of the system times the temperature T. That expresses the fact that once energy is in a highly-entropic form, there’s nothing useful we can do with it any more. So the total internal energy is the free energy plus the useless energy,

Our piston starts in a boring equilibrium configuration a, but we’re not going to let it just sit there. Instead, we’re going to push in the piston, decreasing the volume inside, ending up in configuration b. This squeezes the gas together, and we expect that the total amount of energy will go up. It will typically cost us energy to do this, of course, and we refer to that energy as the work W_ab we do when we push the piston from a to b.

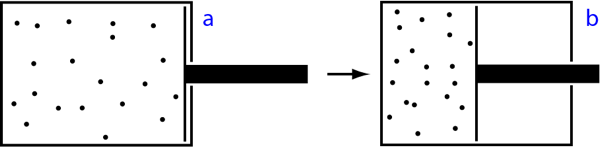
Remember that when we’re done pushing, the system might have heated up a bit, but we let it exchange heat Q with the environment to return to the temperature T. So three things happen when we do our work on the piston: (1) the free energy of the system changes; (2) the entropy changes, and therefore the useless energy; and (3) heat is exchanged with the environment. In total we have

(There is no ΔT, because T is the temperature of the environment, which stays fixed.) The Second Law of Thermodynamics says that entropy increases (or stays constant) in closed systems. Our system isn’t closed, since it might leak heat to the environment. But really the Second Law says that the total of the last two terms on the right-hand side of this equation add up to a positive number; in other words, the increase in entropy will more than compensate for the loss of heat. (Alternatively, you can lower the entropy of a bottle of champagne by putting it in a refrigerator and letting it cool down; no laws of physics are violated.) One way of stating the Second Law for situations such as this is therefore

The work we do on the system is greater than or equal to the change in free energy from beginning to end. We can make this inequality into an equality if we act as efficiently as possible, minimizing the entropy/heat production: that’s an adiabatic process, and in practical terms amounts to moving the piston as gradually as possible, rather than giving it a sudden jolt. That’s the limit in which the process is reversible: we can get the same energy out as we put in, just by going backwards.

Awesome. But the language we’re speaking here is that of classical thermodynamics, which we all know is the limit of statistical mechanics when we have many particles. Let’s be a little more modern and open-minded, and take seriously the fact that our gas is actually a collection of particles in random motion. Because of that randomness, there will be fluctuations over and above the “typical” behavior we’ve been describing. Maybe, just by chance, all of the gas molecules happen to be moving away from our piston just as we move it, so we don’t have to do any work at all; alternatively, maybe there are more than the usual number of molecules hitting the piston, so we have to do more work than usual. The Jarzynski Equality, derived 20 years ago by Christopher Jarzynski, is a way of saying something about those fluctuations.

One simple way of taking our thermodynamic version of the Second Law (3) and making it still hold true in a world of fluctuations is simply to say that it holds true on average. To denote an average over all possible things that could be happening in our system, we write angle brackets around the quantity in question. So a more precise statement would be that the average work we do is greater than or equal to the change in free energy:

(We don’t need angle brackets around ΔF, because F is determined completely by the equilibrium properties of the initial and final states a and b; it doesn’t fluctuate.) Let me multiply both sides by -1, which means we  need to flip the inequality sign to go the other way around:

Next I will exponentiate both sides of the inequality. Note that this keeps the inequality sign going the same way, because the exponential is a monotonically increasing function; if x is less than y, we know that e^x is less than e^y.

(More typically we will see the exponents divided by kT, where k is Boltzmann’s constant, but for simplicity I’m using units where kT = 1.)

Jarzynski’s equality is the following remarkable statement: in equation (6), if we exchange  the exponential of the average work for the average of the exponential of the work , we get a precise equality, not merely an inequality:

That’s the Jarzynski Equality: the average, over many trials, of the exponential of minus the work done, is equal to the exponential of minus the free energies between the initial and final states. It’s a stronger statement than the Second Law, just because it’s an equality rather than an inequality.

In fact, we can derive the Second Law from the Jarzynski equality, using a math trick known as Jensen’s inequality. For our purposes, this says that the exponential of an average is less than the average of an exponential, . Thus we immediately get

as we had before. Then just take the log of both sides to get , which is one way of writing the Second Law.

So what does it mean? As we said, because of fluctuations, the work we needed to do on the piston will sometimes be a bit less than or a bit greater than the average, and the Second Law says that the average will be greater than the difference in free energies from beginning to end. Jarzynski’s Equality says there is a quantity, the exponential of minus the work, that averages out to be exactly the exponential of minus the free-energy difference. The function is convex and decreasing as a function of W. A fluctuation where W is lower than average, therefore, contributes a greater shift to the average of than a corresponding fluctuation where W is higher than average. To satisfy the Jarzynski Equality, we must have more fluctuations upward in W than downward in W, by a precise amount. So on average, we’ll need to do more work than the difference in free energies, as the Second Law implies.

It’s a remarkable thing, really. Much of conventional thermodynamics deals with inequalities, with equality being achieved only in adiabatic processes happening close to equilibrium. The Jarzynski Equality is fully non-equilibrium, achieving equality no matter how dramatically we push around our piston. It tells us not only about the average behavior of statistical systems, but about the full ensemble of possibilities for individual trajectories around that average.

The Jarzynski Equality has launched a mini-revolution in nonequilibrium statistical mechanics, the news of which hasn’t quite trickled to the outside world as yet. It’s one of a number of relations, collectively known as “fluctuation theorems,” which also include the Crooks Fluctuation Theorem, not to mention our own Bayesian Second Law of Thermodynamics. As our technological and experimental capabilities reach down to scales where the fluctuations become important, our theoretical toolbox has to keep pace. And that’s happening: the Jarzynski equality isn’t just imagination, it’s been experimentally tested and verified. (Of course, I remain just a poor theorist myself, so if you want to understand this image from the experimental paper, you’ll have to talk to someone who knows more about Raman spectroscopy than I do.)