Search Results for: boltzman

This year we give thanks for one of the very few clues we have to the quantum nature of spacetime: black hole entropy. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, the Fourier Transform, Riemannian Geometry, the speed of light, the Jarzynski equality, the moons of Jupiter, and space.)

Black holes are regions of spacetime where, according to the rules of Einstein’s theory of general relativity, the curvature of spacetime is so dramatic that light itself cannot escape. Physical objects (those that move at or more slowly than the speed of light) can pass through the “event horizon” that defines the boundary of the black hole, but they never escape back to the outside world. Black holes are therefore black — even light cannot escape — thus the name. At least that would be the story according to classical physics, of which general relativity is a part. Adding quantum ideas to the game changes things in important ways. But we have to be a bit vague — “adding quantum ideas to the game” rather than “considering the true quantum description of the system” — because physicists don’t yet have a fully satisfactory theory that includes both quantum mechanics and gravity.

The story goes that in the early 1970’s, James Bardeen, Brandon Carter, and Stephen Hawking pointed out an analogy between the behavior of black holes and the laws of good old thermodynamics. For example, the Second Law of Thermodynamics (“Entropy never decreases in closed systems”) was analogous to Hawking’s “area theorem”: in a collection of black holes, the total area of their event horizons never decreases over time. Jacob Bekenstein, who at the time was a graduate student working under John Wheeler at Princeton, proposed to take this analogy more seriously than the original authors had in mind. He suggested that the area of a black hole’s event horizon really is its entropy, or at least proportional to it.

This annoyed Hawking, who set out to prove Bekenstein wrong. After all, if black holes have entropy then they should also have a temperature, and objects with nonzero temperatures give off blackbody radiation, but we all know that black holes are black. But he ended up actually proving Bekenstein right; black holes do have entropy, and temperature, and they even give off radiation. We now refer to the entropy of a black hole as the “Bekenstein-Hawking entropy.” (It is just a useful coincidence that the two gentlemen’s initials, “BH,” can also stand for “black hole.”)

Consider a black hole whose area of its event horizon is . Then its Bekenstein-Hawking entropy is

   

where is the speed of light, is Newton’s constant of gravitation, and is Planck’s constant of quantum mechanics. A simple formula, but already intriguing, as it seems to combine relativity (), gravity (), and quantum mechanics () into a single expression. That’s a clue that whatever is going on here, it something to do with quantum gravity. And indeed, understanding black hole entropy and its implications has been a major focus among theoretical physicists for over four decades now, including the holographic principle, black-hole complementarity, the AdS/CFT correspondence, and the many investigations of the information-loss puzzle.

But there exists a prior puzzle: what is the black hole entropy, anyway? What physical quantity does it describe?

Entropy itself was invented as part of the development of thermodynamics is the mid-19th century, as a way to quantify the transformation of energy from a potentially useful form (like fuel, or a coiled spring) into useless heat, dissipated into the environment. It was what we might call a “phenomenological” notion, defined in terms of macroscopically observable quantities like heat and temperature, without any more fundamental basis in a microscopic theory. But more fundamental definitions came soon thereafter, once people like Maxwell and Boltzmann and Gibbs started to develop statistical mechanics, and showed that the laws of thermodynamics could be derived from more basic ideas of atoms and molecules.

Hawking’s derivation of black hole entropy was in the phenomenological vein. He showed that black holes give off radiation at a certain temperature, and then used the standard thermodynamic relations between entropy, energy, and temperature to derive his entropy formula. But this leaves us without any definite idea of what the entropy actually represents.

One of the reasons why entropy is thought of as a confusing concept is because there is more than one notion that goes under the same name. To dramatically over-simplify the situation, let’s consider three different ways of relating entropy to microscopic physics, named after three famous physicists:

• Boltzmann entropy says that we take a system with many small parts, and divide all the possible states of that system into “macrostates,” so that two “microstates” are in the same macrostate if they are macroscopically indistinguishable to us. Then the entropy is just (the logarithm of) the number of microstates in whatever macrostate the system is in.
• Gibbs entropy is a measure of our lack of knowledge. We imagine that we describe the system in terms of a probability distribution of what microscopic states it might be in. High entropy is when that distribution is very spread-out, and low entropy is when it is highly peaked around some particular state.
• von Neumann entropy is a purely quantum-mechanical notion. Given some quantum system, the von Neumann entropy measures how much entanglement there is between that system and the rest of the world.

These seem like very different things, but there are formulas that relate them to each other in the appropriate circumstances. The common feature is that we imagine a system has a lot of microscopic “degrees of freedom” (jargon for “things that can happen”), which can be in one of a large number of states, but we are describing it in some kind of macroscopic coarse-grained way, rather than knowing what its exact state actually is. The Boltzmann and Gibbs entropies worry people because they seem to be subjective, requiring either some seemingly arbitrary carving of state space into macrostates, or an explicit reference to our personal state of knowledge. The von Neumann entropy is at least an objective fact about the system. You can relate it to the others by analogizing the wave function of a system to a classical microstate. Because of entanglement, a quantum subsystem generally cannot be described by a single wave function; the von Neumann entropy measures (roughly) how many different quantum must be involved to account for its entanglement with the outside world.

So which, if any, of these is the black hole entropy? To be honest, we’re not sure. Most of us think the black hole entropy is a kind of von Neumann entropy, but the details aren’t settled.

One clue we have is that the black hole entropy is proportional to the area of the event horizon. For a while this was thought of as a big, surprising thing, since for something like a box of gas, the entropy is proportional to its total volume, not the area of its boundary. But people gradually caught on that there was never any reason to think of black holes like boxes of gas. In quantum field theory, regions of space have a nonzero von Neumann entropy even in empty space, because modes of quantum fields inside the region are entangled with those outside. The good news is that this entropy is (often, approximately) proportional to the area of the region, for the simple reason that field modes near one side of the boundary are highly entangled with modes just on the other side, and not very entangled with modes far away. So maybe the black hole entropy is just like the entanglement entropy of a region of empty space?

Would that it were so easy. Two things stand in the way. First, Bekenstein noticed another important feature of black holes: not only do they have entropy, but they have the most entropy that you can fit into a region of a fixed size (the Bekenstein bound). That’s very different from the entanglement entropy of a region of empty space in quantum field theory, where it is easy to imagine increasing the entropy by creating extra entanglement between degrees of freedom deep in the interior and those far away. So we’re back to being puzzled about why the black hole entropy is proportional to the area of the event horizon, if it’s the most entropy a region can have. That’s the kind of reasoning that leads to the holographic principle, which imagines that we can think of all the degrees of freedom inside the black hole as “really” living on the boundary, rather than being uniformly distributed inside. (There is a classical manifestation of this philosophy in the membrane paradigm for black hole astrophysics.)

The second obstacle to simply interpreting black hole entropy as entanglement entropy of quantum fields is the simple fact that it’s a finite number. While the quantum-field-theory entanglement entropy is proportional to the area of the boundary of a region, the constant of proportionality is infinity, because there are an infinite number of quantum field modes. So why isn’t the entropy of a black hole equal to infinity? Maybe we should think of the black hole entropy as measuring the amount of entanglement over and above that of the vacuum (called the Casini entropy). Maybe, but then if we remember Bekenstein’s argument that black holes have the most entropy we can attribute to a region, all that infinite amount of entropy that we are ignoring is literally inaccessible to us. It might as well not be there at all. It’s that kind of reasoning that leads some of us to bite the bullet and suggest that the number of quantum degrees of freedom in spacetime is actually a finite number, rather than the infinite number that would naively be implied by conventional non-gravitational quantum field theory.

So — mysteries remain! But it’s not as if we haven’t learned anything. The very fact that black holes have entropy of some kind implies that we can think of them as collections of microscopic degrees of freedom of some sort. (In string theory, in certain special circumstances, you can even identify what those degrees of freedom are.) That’s an enormous change from the way we would think about them in classical (non-quantum) general relativity. Black holes are supposed to be completely featureless (they “have no hair,” another idea of Bekenstein’s), with nothing going on inside them once they’ve formed and settled down. Quantum mechanics is telling us otherwise. We haven’t fully absorbed the implications, but this is surely a clue about the ultimate quantum nature of spacetime itself. Such clues are hard to come by, so for that we should be thankful.

This year we give thanks for a simple but profound principle of statistical mechanics that extends the famous Second Law of Thermodynamics: the Jarzynski Equality. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, the Fourier Transform, Riemannian Geometry, and the speed of light.)

The Second Law says that entropy increases in closed systems. But really it says that entropy usually increases; thermodynamics is the limit of statistical mechanics, and in the real world there can be rare but inevitable fluctuations around the typical behavior. The Jarzynski Equality is a way of quantifying such fluctuations, which is increasingly important in the modern world of nanoscale science and biophysics.

Our story begins, as so many thermodynamic tales tend to do, with manipulating a piston containing a certain amount of gas. The gas is of course made of a number of jiggling particles (atoms and molecules). All of those jiggling particles contain energy, and we call the total amount of that energy the internal energy U of the gas. Let’s imagine the whole thing is embedded in an environment (a “heat bath”) at temperature T. That means that the gas inside the piston starts at temperature T, and after we manipulate it a bit and let it settle down, it will relax back to T by exchanging heat with the environment as necessary.

Finally, let’s divide the internal energy into “useful energy” and “useless energy.” The useful energy, known to the cognoscenti as the (Helmholtz) free energy and denoted by F, is the amount of energy potentially available to do useful work. For example, the pressure in our piston may be quite high, and we could release it to push a lever or something. But there is also useless energy, which is just the entropy S of the system times the temperature T. That expresses the fact that once energy is in a highly-entropic form, there’s nothing useful we can do with it any more. So the total internal energy is the free energy plus the useless energy,

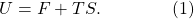
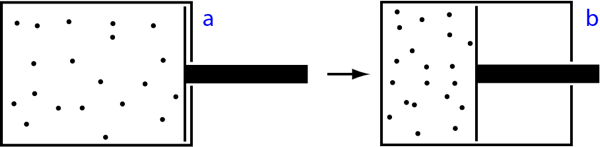
Our piston starts in a boring equilibrium configuration a, but we’re not going to let it just sit there. Instead, we’re going to push in the piston, decreasing the volume inside, ending up in configuration b. This squeezes the gas together, and we expect that the total amount of energy will go up. It will typically cost us energy to do this, of course, and we refer to that energy as the work W_ab we do when we push the piston from a to b.

Remember that when we’re done pushing, the system might have heated up a bit, but we let it exchange heat Q with the environment to return to the temperature T. So three things happen when we do our work on the piston: (1) the free energy of the system changes; (2) the entropy changes, and therefore the useless energy; and (3) heat is exchanged with the environment. In total we have

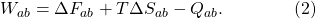
(There is no ΔT, because T is the temperature of the environment, which stays fixed.) The Second Law of Thermodynamics says that entropy increases (or stays constant) in closed systems. Our system isn’t closed, since it might leak heat to the environment. But really the Second Law says that the total of the last two terms on the right-hand side of this equation add up to a positive number; in other words, the increase in entropy will more than compensate for the loss of heat. (Alternatively, you can lower the entropy of a bottle of champagne by putting it in a refrigerator and letting it cool down; no laws of physics are violated.) One way of stating the Second Law for situations such as this is therefore

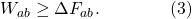
The work we do on the system is greater than or equal to the change in free energy from beginning to end. We can make this inequality into an equality if we act as efficiently as possible, minimizing the entropy/heat production: that’s an adiabatic process, and in practical terms amounts to moving the piston as gradually as possible, rather than giving it a sudden jolt. That’s the limit in which the process is reversible: we can get the same energy out as we put in, just by going backwards.

Awesome. But the language we’re speaking here is that of classical thermodynamics, which we all know is the limit of statistical mechanics when we have many particles. Let’s be a little more modern and open-minded, and take seriously the fact that our gas is actually a collection of particles in random motion. Because of that randomness, there will be fluctuations over and above the “typical” behavior we’ve been describing. Maybe, just by chance, all of the gas molecules happen to be moving away from our piston just as we move it, so we don’t have to do any work at all; alternatively, maybe there are more than the usual number of molecules hitting the piston, so we have to do more work than usual. The Jarzynski Equality, derived 20 years ago by Christopher Jarzynski, is a way of saying something about those fluctuations.

One simple way of taking our thermodynamic version of the Second Law (3) and making it still hold true in a world of fluctuations is simply to say that it holds true on average. To denote an average over all possible things that could be happening in our system, we write angle brackets around the quantity in question. So a more precise statement would be that the average work we do is greater than or equal to the change in free energy:

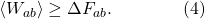
(We don’t need angle brackets around ΔF, because F is determined completely by the equilibrium properties of the initial and final states a and b; it doesn’t fluctuate.) Let me multiply both sides by -1, which means we  need to flip the inequality sign to go the other way around:

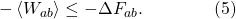
Next I will exponentiate both sides of the inequality. Note that this keeps the inequality sign going the same way, because the exponential is a monotonically increasing function; if x is less than y, we know that e^x is less than e^y.

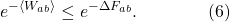
(More typically we will see the exponents divided by kT, where k is Boltzmann’s constant, but for simplicity I’m using units where kT = 1.)

Jarzynski’s equality is the following remarkable statement: in equation (6), if we exchange  the exponential of the average work 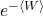for the average of the exponential of the work 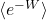, we get a precise equality, not merely an inequality:

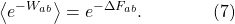
That’s the Jarzynski Equality: the average, over many trials, of the exponential of minus the work done, is equal to the exponential of minus the free energies between the initial and final states. It’s a stronger statement than the Second Law, just because it’s an equality rather than an inequality.

In fact, we can derive the Second Law from the Jarzynski equality, using a math trick known as Jensen’s inequality. For our purposes, this says that the exponential of an average is less than the average of an exponential, 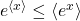. Thus we immediately get

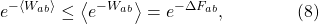
as we had before. Then just take the log of both sides to get 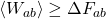, which is one way of writing the Second Law.

So what does it mean? As we said, because of fluctuations, the work we needed to do on the piston will sometimes be a bit less than or a bit greater than the average, and the Second Law says that the average will be greater than the difference in free energies from beginning to end. Jarzynski’s Equality says there is a quantity, the exponential of minus the work, that averages out to be exactly the exponential of minus the free-energy difference. The function 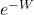is convex and decreasing as a function of W. A fluctuation where W is lower than average, therefore, contributes a greater shift to the average of 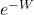than a corresponding fluctuation where W is higher than average. To satisfy the Jarzynski Equality, we must have more fluctuations upward in W than downward in W, by a precise amount. So on average, we’ll need to do more work than the difference in free energies, as the Second Law implies.

It’s a remarkable thing, really. Much of conventional thermodynamics deals with inequalities, with equality being achieved only in adiabatic processes happening close to equilibrium. The Jarzynski Equality is fully non-equilibrium, achieving equality no matter how dramatically we push around our piston. It tells us not only about the average behavior of statistical systems, but about the full ensemble of possibilities for individual trajectories around that average.

The Jarzynski Equality has launched a mini-revolution in nonequilibrium statistical mechanics, the news of which hasn’t quite trickled to the outside world as yet. It’s one of a number of relations, collectively known as “fluctuation theorems,” which also include the Crooks Fluctuation Theorem, not to mention our own Bayesian Second Law of Thermodynamics. As our technological and experimental capabilities reach down to scales where the fluctuations become important, our theoretical toolbox has to keep pace. And that’s happening: the Jarzynski equality isn’t just imagination, it’s been experimentally tested and verified. (Of course, I remain just a poor theorist myself, so if you want to understand this image from the experimental paper, you’ll have to talk to someone who knows more about Raman spectroscopy than I do.)