Kim Boddy and I have just written a new paper, with maybe my favorite title ever.
Can the Higgs Boson Save Us From the Menace of the Boltzmann Brains?
Kimberly K. Boddy, Sean M. Carroll
(Submitted on 21 Aug 2013)The standard ΛCDM model provides an excellent fit to current cosmological observations but suffers from a potentially serious Boltzmann Brain problem. If the universe enters a de Sitter vacuum phase that is truly eternal, there will be a finite temperature in empty space and corresponding thermal fluctuations. Among these fluctuations will be intelligent observers, as well as configurations that reproduce any local region of the current universe to arbitrary precision. We discuss the possibility that the escape from this unacceptable situation may be found in known physics: vacuum instability induced by the Higgs field. Avoiding Boltzmann Brains in a measure-independent way requires a decay timescale of order the current age of the universe, which can be achieved if the top quark pole mass is approximately 178 GeV. Otherwise we must invoke new physics or a particular cosmological measure before we can consider ΛCDM to be an empirical success.
We apply some far-out-sounding ideas to very down-to-Earth physics. Among other things, we’re suggesting that the mass of the top quark might be heavier than most people think, and that our universe will decay in another ten billion years or so. Here’s a somewhat long-winded explanation.
A room full of monkeys, hitting keys randomly on a typewriter, will eventually bang out a perfect copy of Hamlet. Assuming, of course, that their typing is perfectly random, and that it keeps up for a long time. An extremely long time indeed, much longer than the current age of the universe. So this is an amusing thought experiment, not a viable proposal for creating new works of literature (or old ones).
There’s an interesting feature of what these thought-experiment monkeys end up producing. Let’s say you find a monkey who has just typed Act I of Hamlet with perfect fidelity. You might think “aha, here’s when it happens,” and expect Act II to come next. But by the conditions of the experiment, the next thing the monkey types should be perfectly random (by which we mean, chosen from a uniform distribution among all allowed typographical characters), and therefore independent of what has come before. The chances that you will actually get Act II next, just because you got Act I, are extraordinarily tiny. For every one time that your monkeys type Hamlet correctly, they will type it incorrectly an enormous number of times — small errors, large errors, all of the words but in random order, the entire text backwards, some scenes but not others, all of the lines but with different characters assigned to them, and so forth. Given that any one passage matches the original text, it is still overwhelmingly likely that the passages before and after are random nonsense.
That’s the Boltzmann Brain problem in a nutshell. Replace your typing monkeys with a box of atoms at some temperature, and let the atoms randomly bump into each other for an indefinite period of time. Almost all the time they will be in a disordered, high-entropy, equilibrium state. Eventually, just by chance, they will take the form of a smiley face, or Michelangelo’s David, or absolutely any configuration that is compatible with what’s inside the box. If you wait long enough, and your box is sufficiently large, you will get a person, a planet, a galaxy, the whole universe as we now know it. But given that some of the atoms fall into a familiar-looking arrangement, we still expect the rest of the atoms to be completely random. Just because you find a copy of the Mona Lisa, in other words, doesn’t mean that it was actually painted by Leonardo or anyone else; with overwhelming probability it simply coalesced gradually out of random motions. Just because you see what looks like a photograph, there’s no reason to believe it was preceded by an actual event that the photo purports to represent. If the random motions of the atoms create a person with firm memories of the past, all of those memories are overwhelmingly likely to be false.
This thought experiment was originally relevant because Boltzmann himself (and before him Lucretius, Hume, etc.) suggested that our world might be exactly this: a big box of gas, evolving for all eternity, out of which our current low-entropy state emerged as a random fluctuation. As was pointed out by Eddington, Feynman, and others, this idea doesn’t work, for the reasons just stated; given any one bit of universe that you might want to make (a person, a solar system, a galaxy, and exact duplicate of your current self), the rest of the world should still be in a maximum-entropy state, and it clearly is not. This is called the “Boltzmann Brain problem,” because one way of thinking about it is that the vast majority of intelligent observers in the universe should be disembodied brains that have randomly fluctuated out of the surrounding chaos, rather than evolving conventionally from a low-entropy past. That’s not really the point, though; the real problem is that such a fluctuation scenario is cognitively unstable — you can’t simultaneously believe it’s true, and have good reason for believing its true, because it predicts that all the “reasons” you think are so good have just randomly fluctuated into your head!
All of which would seemingly be little more than fodder for scholars of intellectual history, now that we know the universe is not an eternal box of gas. The observable universe, anyway, started a mere 13.8 billion years ago, in a very low-entropy Big Bang. That sounds like a long time, but the time required for random fluctuations to make anything interesting is enormously larger than that. (To make something highly ordered out of something with entropy S, you have to wait for a time of order eS. Since macroscopic objects have more than 1023 particles, S is at least that large. So we’re talking very long times indeed, so long that it doesn’t matter whether you’re measuring in microseconds or billions of years.) Besides, the universe is not a box of gas; it’s expanding and emptying out, right?
Ah, but things are a bit more complicated than that. We now know that the universe is not only expanding, but also accelerating. The simplest explanation for that — not the only one, of course — is that empty space is suffused with a fixed amount of vacuum energy, a.k.a. the cosmological constant. Vacuum energy doesn’t dilute away as the universe expands; there’s nothing in principle from stopping it from lasting forever. So even if the universe is finite in age now, there’s nothing to stop it from lasting indefinitely into the future.
But, you’re thinking, doesn’t the universe get emptier and emptier as it expands, leaving no particles to fluctuate? Only up to a point. A universe with vacuum energy accelerates forever, and as a result we are surrounded by a cosmological horizon — objects that are sufficiently far away can never get to us or even send signals, as the space in between expands too quickly. And, as Stephen Hawking and Gary Gibbons pointed out in the 1970’s, such a cosmology is similar to a black hole: there will be radiation associated with that horizon, with a constant temperature.
In other words, a universe with a cosmological constant is like a box of gas (the size of the horizon) which lasts forever with a fixed temperature. Which means there are random fluctuations. If we wait long enough, some region of the universe will fluctuate into absolutely any configuration of matter compatible with the local laws of physics. Atoms, viruses, people, dragons, what have you. The room you are in right now (or the atmosphere, if you’re outside) will be reconstructed, down to the slightest detail, an infinite number of times in the future. In the overwhelming majority of times that your local environment does get created, the rest of the universe will look like a high-entropy equilibrium state (in this case, empty space with a tiny temperature). All of those copies of you will think they have reliable memories of the past and an accurate picture of what the external world looks like — but they would be wrong. And you could be one of them.
That would be bad.
Discussions of the Boltzmann Brain problem typically occur in the context of speculative ideas like eternal inflation and the multiverse. (Not that there’s anything wrong with that.) And, let’s admit it, the very idea of orderly configurations of matter spontaneously fluctuating out of chaos sounds a bit loopy, as critics have noted. But everything I’ve just said is based on physics we think we understand: quantum field theory, general relativity, and the cosmological constant. This is the real world, baby. Of course it’s possible that we are making some subtle mistake about how quantum field theory works, but that is more speculative than taking the straightforward prediction seriously.
Modern cosmologists have a favorite default theory of the universe, labeled ΛCDM, where “Λ” stands for the cosmological constant and “CDM” for Cold Dark Matter. What we’re pointing out is that ΛCDM, the current leading candidate for an accurate description of the cosmos, can’t be right all by itself. It has a Boltzmann Brain problem, and is therefore cognitively unstable, and unacceptable as a physical theory.
Can we escape this unsettling conclusion? Sure, by tweaking the physics a little bit. The simplest route is to make the vacuum energy not really a constant, e.g. by imagining that it is a dynamical field (quintessence). But that has it’s own problems, associated with very tiny fine-tuned parameters. A more robust scenario would be to invoke quantum vacuum decay. Maybe the vacuum energy is temporarily constant, but there is another vacuum state out there in field space with an even lower energy, to which we can someday make a transition. What would happen is that tiny bubbles of the lower-energy configuration would appear via quantum tunneling; these would rapidly grow at the speed of light. If the energy of the other vacuum state were zero or negative, we wouldn’t have this pesky Boltzmann Brain problem to deal with.
Fine, but it seems to invoke some speculative physics, in the form of new fields and a new quantum vacuum state. Is there any way to save ΛCDM without invoking new physics at all?
The answer is — maybe! This is where Kim and I come in, although some of the individual pieces of our puzzle were previously put together by other authors. The first piece is a fun bit of physics that hit the news media earlier this year: the possibility that the Higgs field can itself support another vacuum state other than the one we live in. (The reason why this is true is a bit subtle, but it comes down to renormalization group effects.) That’s right: without introducing any new physics at all, it’s possible that the Higgs field will decay via bubble nucleation some time in the future, dramatically changing the physics of our universe. The whole reason the Higgs is interesting is that it has a nonzero value even in empty space; what we’re saying here is that there might be an even larger value with an even lower energy. We’re not there now, but we could get there via a phase transition. And that, Kim and I point out, has a possibility of saving us from the Boltzmann Brain problem.
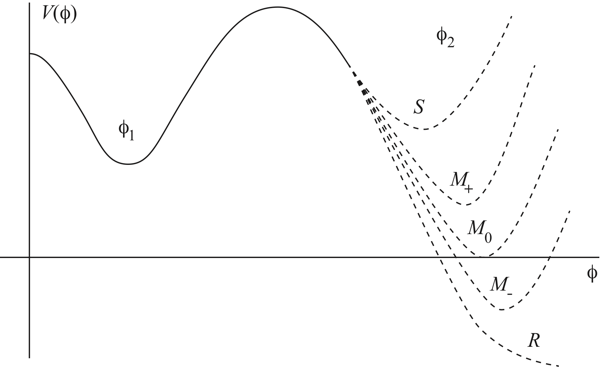
Imagine that the plot of “energy of empty space” versus “value of the Higgs field” looks like this.
φ is the value of the Higgs field. Our current location is φ1, where there is some positive energy. Somewhere out at a much larger value φ2, with a different energy. If the energy at φ2 is greater than at φ1, our current vacuum is stable. If it’s any lower value, we are “metastable”; our current situation can last for a while, but eventually we will transition to a different state. Or the Higgs can have no other vacuum far away, a “runaway” solution. (Note that if the energy in the other state is negative, space inside the bubbles of new vacuum will actually collapse to a Big Crunch rather than expanding.)
But even if that’s true, it’s not good enough by itself. Imagine that there is another vacuum state, and that we can nucleate bubbles that create regions of that new phase. The bubbles will expand at nearly the speed of light — but will they ever bump into other bubbles, and complete the transition from our current phase to the new one? Will the transition “percolate,” in other words? The answer is only “yes” if the bubbles are created rapidly enough. If they are created too slowly, the cosmological horizons come into play — spacetime expands so fast that two random bubbles will never meet each other, and the volume of space left in the original phase (the one we’re in now) keeps growing without bound. (This is the “graceful exit problem” of Alan Guth’s original inflationary-universe scenario.)
So given that the Higgs field might support a different quantum vacuum, we have two questions. First, is our current vacuum stable, or is there actually a lower-energy vacuum to which we can transition? Second, if there is a lower-energy vacuum, does our vacuum decay fast enough that the transition percolates, or do we get stuck with an ever-increasing amount of space in the current phase?
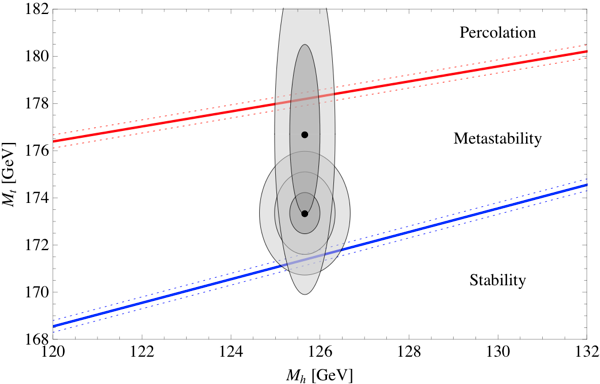
The answers depend on the precise value of the parameters that specify the Standard Model of particle physics, and therefore determine the renormalized Higgs potential. In particular, two parameters turn out to be the most important: the mass of the Higgs itself, and the mass of the top quark. We’ve measured both, but of course our measurements only have a certain precision. Happily, the answers to the two questions we are asking (is our vacuum stable, and does it decay quickly enough to percolate) have already been calculated by other groups: the stability question has been tackled (most recently, after much earlier work) by Buttazzo et al., and the percolation question has been tackled by Arkani-Hamed et al. Here are the answers, plotted in the parameter space defined by the Higgs mass and the top mass. (Dotted lines represent uncertainties in another parameter, the QCD coupling constant.)
We are interested in the two diagonal lines. If you are below the bottom line, the Higgs field is stable, and you definitely have a Boltzmann Brain problem. If you are in between the two lines, bubbles nucleate and grow, but they don’t percolate, and our current state survives. (Whether or not there is a Boltzmann-Brain problem is then measure-dependent, see below.) If you are above the top line, bubbles nucleate quite quickly, and the transition percolates just fine. However, in that region the bubbles actually nucleate too fast; the phase transition should have already happened! The favored part of this diagram is actually the top diagonal line itself; that’s the only region in which we can definitely avoid Boltzmann Brains, but can still be here to have this conversation.
We’ve also plotted two sets of ellipses, corresponding to the measured values of the Higgs and top masses. The most recent LHC numbers put the Higgs mass at 125.66 ± 0.34 GeV, which is quite good precision. The most recent consensus number for the top quark mass is 173.20 ± 0.87 GeV. Combining these results gives the lower of our two sets of ellipses, where we have plotted one-sigma, two-sigma, and three-sigma contours. We see that the central value is in the “metastable” regime, where there can be bubble nucleation but the phase transition is not fast enough to percolate. The error bars do extend into the stable region, however.
Interestingly, there has been a bit of controversy over whether this measured value of the top quark mass is the same as the parameter we use in calculating the potential energy of the Higgs field (the so-called “pole” mass). This is a discussion that is a bit outside my expertise, but a very recent paper by the CMS collaboration tries to measure the number we actually want, and comes up with much looser error bars: 176.7 ± 3.6 GeV. That’s where we got our other set of ellipses (one-sigma and two-sigma) from. If we take these numbers at face value, it’s possible that the top quark could be up there at 178 GeV, which would be enough to live on the viability line, where the phase transition will happen quickly but not too quickly. My bet would be that the consensus numbers are close to correct, but let’s put it this way: we are predicting that either the pole mass of the top quark turns out to be 178 GeV, or there is some new physics that kicks in to destabilize our current vacuum.
I was a bit unclear about what happens in the vast “metastable” region between stability and percolation. That’s because the situation is actually a bit unclear. Naively, in that region the volume of space in our current vacuum grows without bound, and Boltzmann Brains will definitely dominate. But a similar situation arises in eternal inflation, leading to what’s called the cosmological measure problem. The meat of our paper was not actually plotting a couple of curves that other people had calculated, but attempting to apply approaches to the eternal-inflation measure problem to our real-world situation. The results were a bit inconclusive. In most measures, it’s safe to say, the Boltzmann Brain problem is as bad as you might have feared. But there is at least one — a modified causal-patch measure with terminal vacua, if you must know — in which the problem is avoided. I’m not sure if there is some principled reason to believe in this measure other than “it gives an acceptable answer,” but our results suggest that understanding cosmological measure theory may be important even if you don’t believe in eternal inflation.
A final provocative observation that I’ve been saving for last. The safest place to be is on the top diagonal line in our diagram, where we have bubbles nucleating fast enough to percolate but not so fast that they should have already happened. So what does it mean, “fast enough to percolate,” anyway? Well, roughly, it means you should be making new bubbles approximately once per current lifetime of our universe. (Don Page has done a slightly more precise estimate of 20 billion years.) On the one hand, that’s quite a few billion years; it’s not like we should rush out and buy life insurance. On the other hand, it’s not that long. It means that roughly half of the lifetime of our current universe has already happened. And the transition could happen much faster — it could be tomorrow or next year, although the chances are quite tiny.
For our purposes, avoiding Boltzmann Brains, we want the transition to happen quickly. Amusingly, most of the existing particle-physics literature on decay of the Higgs field seems to take the attitude that we should want it to be completely stable — otherwise the decay of the Higgs will destroy the universe! It’s true, but we’re pointing out that this is a feature, not a bug, as we need to destroy the universe (or at least the state its currently in) to save ourselves from the invasion of the Boltzmann Brains.
All of this, of course, assumes there is no new physics at higher energies that would alter our calculations, which seems an unlikely assumption. So the alternatives are: new physics, an improved understanding of the cosmological measure problem, or a prediction that the top quark is really 178 GeV. A no-lose scenario, really.
Great riff, Sean :3
(you probably play a mean game of nomic)
Outside of thought experiments, are there any processes that are perfectly random?
Sean, what about the old standard QFT argument against tunnelling of the Higgs field into another vacuum?
IIRC, the argument roughly went like this — there is a finite probability that the vacuum state can tunnel from one local minimum of the Higgs potential into another one (perhaps lower, more stable one). This is the ordinary probability for the QM tunnel-effect. But in order to have a “bubble” of space with a different vacuum, one needs to calculate the total probability for the tunneling for all points in the volume of the bubble. If one assumes that QFT is fundamental to all scales, this total probability is equal to the product of those per-point probabilities, where the product is taken over an uncountably-infinitely many points of space inside the bubble. And this cannot be anything but zero, since it is a number smaller than one raised to a continuum-infinite power.
Therefore, the argument is that the total probability for a phase transition must be zero, since the spacetime manifold has way too many points in which this should happen. This is in contrast to the situation in solid state physics, where these transitions happen on regular basis — but there they are working with a lattice of a finite number of cells, and this probability is consequently still finite. But in a system with uncountably infinitely many degrees of freedom (i.e. in QFT), such a transition is forbidden by the “total number” of points present on a spacetime manifold.
So, how do you get around this issue?
Best, 🙂
Marko
Marko– That’s basically the argument that applies to the case when you have degenerate vacua. It’s used to show that the quantum state is based on a single field value, not a superposition of multiple values. But when the energies are different, a phase transition from one to the other is certainly possible (as Coleman’s classic “fate of the false vacuum” papers showed).
Love this post and discussion of the Boltzmann brain problem. I’m no expert in these fields but I always think about the different categories (or classifications) of different infinities that we have and how this relates to tunneling calculations and the probabilities associated with tunneling or emergence of Boltzmann brains.
Aha, I see, thanks for the pointer! 🙂 By the way, I have found the first Coleman’s paper,
http://www.physics.princeton.edu/~steinh/ph564/Coleman.pdf
and I skimmed through it, but apparently not well enough to pinpoint the difference between the degenerate and nondegenerate vacuua. Maybe it is explained better in the second paper, I’ll try to find it tomorrow or so… 🙂
Best, 🙂
Marko
I think I’m missing something fundamental here … what exactly IS the problem with Boltzmann brains? Presumably their rate of formation is extremely low (and hence you need an infinitely old universe before you worry about the problem), so there likely isn’t any experimental data that says that this doesn’t happen. While the work you describe is interesting, it seems like a lot of effort to avoid a prediction (that most observers are Boltzmann brains) just because you’re prefer it weren’t true, rather than because you really have any reason to think that it’s not true.
Ten billion years is rather short (in this context), don’t you think? The blackbody temperature of the universe would still be on the order of 1 K, and I suppose the vacuum energy contribution would also be miniscule. Okay, accuse me of being anthropically biased, but what I’m saying is that ten billion years from now, I think the universe will look more or less as it does now (my local, non-ersatz un-boltzmann brainly, now, that is), and that means the Mayan calendar, when properly renormalized, is right:)
Boltzmann’s Brain– As explained in the post, the problem is that a theory dominated by random fluctuations is cognitively unstable. You can’t simultaneously believe in it, and be justified in believing it. (I’m working on a paper that spells this out in more detail.)
Steverino– Ten billion years is indeed rather short, but that’s what it has to be. If the phase transition doesn’t happen by then, chances are good it will never fully happen.
Re . Boltzmann Brains
The smallest possible universal Turing Machine can be represented in just 37 bits (see my blog : http://www.savory.de/blog_may_12.htm#20120520) , so it’s not going to take TOO long to assemble one of these by chance 🙂 ?
Wikipedia claims the Boltzmann Brains problem is resolved by natural selection; essentially since a simpler life form can evolve into a more complex one, evolved brains are more likely than those “created from scratch”.
http://en.wikipedia.org/wiki/Boltzmann_brains
Wouldn’t a multiverse with vacua of differing lifetimes also ruin this reasoning? Even if this vacuum has a “short” lifetime, others would not.
Finally, wouldn’t the anthropic principle say that even if our vacuum had a shorter half-life than its current age, we wouldn’t be here to observe it if it had already decayed?
I’m sorry, I’m not buying “cognitively unstable” as a valid argument here. There is nothing in the laws of physics that requires that our epistemology be on secure footing. Can you really justify as a fundamental principle to guide our thinking the idea that the universe couldn’t possibly allow the formation of intelligent organisms with false memories and unjustified beliefs? Just because it undermines your epistemology is not good enough to use it as the basis of judging what’s plausible physical law and what isn’t. The universe just doesn’t give a hoot about your epistemology.
I kind of agree with Boltzmann’s Brain, though the style in which he presents it is a bit blunt; not that I have any room to speak. I personally do need further explanation because I don’t really have a deep rooted understanding of the issue, so I’ll be interested in seeing Dr. Carroll further explain this concept.
But my main objection is to the concept of being cognitively unstable. Specifically, I don’t understand how random fluctuations over time differ from orderly evolution. Isn’t orderly evolution the convergence of random fluctuations?
Sean,
I know you’ve expressed support for many worlds before. What are your thoughts on arguments that the vacuum is unstable (or metastable), and we simply live in branches where it hasn’t decayed yet?
Stephen– If the vacuum is metastable, and many-worlds is right, then we certainly do live in a branch where it hasn’t decayed yet!
Higguns– Not exactly. Ordinary evolution is the result of evolution from a lower-entropy past; the kind of evolution we’re talking about here is a random fluctuation from a high-entropy state to a lower-entropy one.
Let me offer an analogy that I think further erodes the usefulness of cognitive stability as a concept … as far as we know there is nothing in the laws of physics that rules out our building an artificial mind, complete with fabricated memories and unjustified beliefs. Indeed, once someone produces the first such AI, many, many more will come into existence, and since a computer simulation runs a lot, lot faster than biological hardware, we could simulate millions or billions of “lives”.
This raises two troubling possibilities. The first is that I may myself be nothing more than a simulation in a computer somewhere, and that the memories and experiences I have are false, planted in my mind by the programmer who made me. The second is that it’s quite plausible that the majority of lives that have ever been “lived” are simulated lives inside computers.
Is it therefore valid for me to conclude that the laws of physics prevent the simulation of minds in this manner, since otherwise my own beliefs about my own life and experiences would be without justification?
Damn. You picked a good objective for the pop-science side of your career, S.C.. I just tried looking around for different perspectives…people are seriously confused; including myself apparently. I get what you’re saying now. I guess I was still stuck in philosophy mode. Do you have any thoughts on the latest headline grabber? http://arxiv.org/abs/1303.6878
Edit: I should say ‘pop-sci’ headline grabber.
Boltzmann, I think you are missing the point. If we were a simulation arising out of molecular chaos, the hypothesis would instantly be falsified in the next second where we observe a continuation of our reality. That’s why we know that we are not and never were Boltzmann brains.
Now if we did allow a universe which allowed them to occur, we face a problem of typicality. Since they are exponentially more likely to occur than regular observers, why are we here and not a BB? Very uncopernican.
Ergo we don’t live in a universe that allows BB to form.
Wow, this is a truly fascinating discussion that unravels lots of cool cosmology after doing all the homework required. It just feels so trivial to have spent my day merely helping a broadway musician who lives 90 miles from 42nd street to successfully figure out how they’re going to undertake the medical treatments that they need to stay alive, and still get to keep playing their music on Broadway. But do call me when it’s time for cocktails; I would so much like to chat.
A very interesting article. Yet, every issue can have many different points of view. One old grandmother who is the expert of *daily* phenomena sees this Boltzmann monkey Brain issue with a very different view, from her “bathtub dirt-pattern model”.
When the body dirt was washed into the bath water, it does not settle on the bottom of the tub uniformly but with some stringy patterns with both closed (water not drain) or opened (water drained) situations. She thus made a “bathtub dirt-pattern model”.
a. The dirt distribution in the tub water is totally uniform (random or symmetric).
b. When two dirt particles collide, they stick together (an interaction).
c. When first two dirt particles collide, the *total* randomness is no more (symmetry-breaking).
d. This symmetry-breaking accelerates the further randomness-reduction (pattern [or order] forms).
She quickly formulates a “Randomness dynamics” —- when the members in a *totally* random system has an *interaction* (of any kind), it (the interaction) will spontaneously break the *totality* of that randomness, and some patterns (or orders) will be formed.
On the other hand, the “Act I of Hamlet” emergence from the Boltzmann monkey Brain is a result of totally random chance, not a result of the Randomness Dynamics. Thus, the “Act I of Hamlet” in the Boltzmann monkey universe is dead, without a life.
Sean Carroll wrote, “In other words, a universe with a cosmological constant is like a box of gas (the size of the horizon) which lasts forever with a fixed temperature. Which means there are random fluctuations. If we wait long enough, some region of the universe will fluctuate into absolutely any configuration of matter compatible with the local laws of physics. Atoms, viruses, people, dragons, what have you. … And, let’s admit it, the very idea of orderly configurations of matter spontaneously fluctuating out of chaos sounds a bit loopy, as critics have noted. But everything I’ve just said is based on physics we think we understand: quantum field theory, general relativity, and the cosmological constant. This is the real world, baby.”
Again, those atoms, viruses spontaneously fluctuating out of a box of chaotic gas in the manner of Boltzmann monkey Brain are also lifeless and meaningless for this old grandmother. That is, the Boltzmann monkey Brain cannot be a part of the reality. Yet, as long as there is an interaction of any kind among the members of that box, the patterns and orders will emergent, not by any random chance but by the randomness breaking.
But by all means, ΛCDM is wrong.
So Sean, it seems that you concede that for those of us who are cognitively unstable, there is no Boltzmann Brains problem!
Pingback: Sean Carroll and Boltzmann Brain | The Great Vindications
I see many holes in the “Boltzmann Brain problem.”
1. The typing monkeys analogy is deeply flawed. Yes the chance a monkey will type act II after typing act I is negligible, but that doesn’t mean that a physical entity brought about by a random fluctuation has negligible chance of continuing as normal. On the contrary, the chances of it disappearing in another fluctuation are negligible, and it will evolve according to usual laws.
2. Ok, so a huge fluctuation is less likely then a small one, but a huge fluctuation may produce greatly more brain-hours for example because the brains won’t instantly suffocate in the empty space, or because it will allow them to multiply, so it’s far from clear that a conscious thought has a higher chance of appearing in a Boltzmann brain then in a human on Earth.
3. Unlikely events do happen. Even if we were to assume (which I don’t agree with) that it is much more likely for an observer to be a small Boltzmann brain fluctuation then part of Earth biosphere an single case where you happened to be a part of biosphere certainly doesn’t prove anything.
4. How do you know you are not a Boltzmann brain? After all you only have access to a single instant, and even that only through your senses, whose reliability you have no way to assess. It’s just as possible you only exist for a fleeting second with false memories and fake sensual impressions, a small fluctuation dreaming of being a part of a huge one.
Given a phase space describing all possible configurations of a system as large as the observable universe, I think it’s clear that the volume of the subset A of the phase space that describes 100 kg of the contents organised as a human observer and the rest organised into fellow observers, planets, stars and galaxies is vastly smaller than the volume of the subset B (containing A) that describes 100 kg of the contents organised as a human observer, and the rest arranged any way at all.
What’s far less clear to me is whether this ratio of volumes reflects the proportion of time the system would spend in A and B. The ergodic hypothesis is the kind of assumption that I’m willing to accept when discussing things like the time an ideal gas would spend occupying a certain cubical fraction of its container, but has it actually been proven as a rigorous theorem for absolutely any subset of phase space?
As AI says, the time evolution of the system in phase space is not like a monkey hitting random keys, which would be uncorrelated from moment to moment. Rather, it’s following the same Hamiltonian flow that keeps us all alive from moment to moment, and which brought us into being in the first place from a low entropy past. It’s not obvious to me that the tiny fraction of phase space trajectories that would involve assembling an observer with false memories out of a cloud of gas isn’t itself so minuscule that it counterbalances the difference in phase space volumes. The phase space volumes are relatively easy to estimate, but short of a rigorous proof that the ergodic theorem applies universally, surely the detailed dynamics of how an observer can actually be formed have some bearing on the matter.
Having said that, I accept that we observe far too much order in the distant universe to believe that we’re a Boltzmann fluctuation in the original sense. It’s hard to see why all of that would be required by most trajectories through phase space that allowed us to be conscious at all.
If there is a flaw in the Boltzmann Brain idea, I think it would have to do with boundary conditions. A living brain has an interface to a low-entropy world (comparatively speaking), while the sort of configuration of matter that might give rise to a Boltzmann Brain has an interface to a high-entropy world. I suspect that the interface has something to do with whether consciousness can form. Furthermore, it may be that certain configurations of matter can only emerge from a very low-entropy past — do we really know all the rules?
However, I don’t buy into B.B.’s argument that cognitive instability doesn’t matter. It does matter if you want to do science. Yes, the Universe doesn’t care about our epistemology. But it doesn’t care whether or not we do science either. If we want to do science then we have to care about epistemology. A Boltzmann Brain can’t do meaningful science if its only sensations are dreams. So if my argument is wrong, and Boltzmann Brains are possible, then unless Sean is right about the vacuum instability, they do represent a problem for us.
AI: “2. Ok, so a huge fluctuation is less likely then a small one, but a huge fluctuation may produce greatly more brain-hours for example because the brains won’t instantly suffocate in the empty space, or because it will allow them to multiply, so it’s far from clear that a conscious thought has a higher chance of appearing in a Boltzmann brain then in a human on Earth.”
If fluctuation F1 is N times larger (spatially or temporally) than fluctuation F2, then it can contain on the order of N times as many consciousness entities. But the number of fluctuations the size of F2 should be on the order of exp(N) times the number of F1-sized fluctuations. F2 wins.