Kim Boddy and I have just written a new paper, with maybe my favorite title ever.
Can the Higgs Boson Save Us From the Menace of the Boltzmann Brains?
Kimberly K. Boddy, Sean M. Carroll
(Submitted on 21 Aug 2013)The standard ΛCDM model provides an excellent fit to current cosmological observations but suffers from a potentially serious Boltzmann Brain problem. If the universe enters a de Sitter vacuum phase that is truly eternal, there will be a finite temperature in empty space and corresponding thermal fluctuations. Among these fluctuations will be intelligent observers, as well as configurations that reproduce any local region of the current universe to arbitrary precision. We discuss the possibility that the escape from this unacceptable situation may be found in known physics: vacuum instability induced by the Higgs field. Avoiding Boltzmann Brains in a measure-independent way requires a decay timescale of order the current age of the universe, which can be achieved if the top quark pole mass is approximately 178 GeV. Otherwise we must invoke new physics or a particular cosmological measure before we can consider ΛCDM to be an empirical success.
We apply some far-out-sounding ideas to very down-to-Earth physics. Among other things, we’re suggesting that the mass of the top quark might be heavier than most people think, and that our universe will decay in another ten billion years or so. Here’s a somewhat long-winded explanation.
A room full of monkeys, hitting keys randomly on a typewriter, will eventually bang out a perfect copy of Hamlet. Assuming, of course, that their typing is perfectly random, and that it keeps up for a long time. An extremely long time indeed, much longer than the current age of the universe. So this is an amusing thought experiment, not a viable proposal for creating new works of literature (or old ones).
There’s an interesting feature of what these thought-experiment monkeys end up producing. Let’s say you find a monkey who has just typed Act I of Hamlet with perfect fidelity. You might think “aha, here’s when it happens,” and expect Act II to come next. But by the conditions of the experiment, the next thing the monkey types should be perfectly random (by which we mean, chosen from a uniform distribution among all allowed typographical characters), and therefore independent of what has come before. The chances that you will actually get Act II next, just because you got Act I, are extraordinarily tiny. For every one time that your monkeys type Hamlet correctly, they will type it incorrectly an enormous number of times — small errors, large errors, all of the words but in random order, the entire text backwards, some scenes but not others, all of the lines but with different characters assigned to them, and so forth. Given that any one passage matches the original text, it is still overwhelmingly likely that the passages before and after are random nonsense.
That’s the Boltzmann Brain problem in a nutshell. Replace your typing monkeys with a box of atoms at some temperature, and let the atoms randomly bump into each other for an indefinite period of time. Almost all the time they will be in a disordered, high-entropy, equilibrium state. Eventually, just by chance, they will take the form of a smiley face, or Michelangelo’s David, or absolutely any configuration that is compatible with what’s inside the box. If you wait long enough, and your box is sufficiently large, you will get a person, a planet, a galaxy, the whole universe as we now know it. But given that some of the atoms fall into a familiar-looking arrangement, we still expect the rest of the atoms to be completely random. Just because you find a copy of the Mona Lisa, in other words, doesn’t mean that it was actually painted by Leonardo or anyone else; with overwhelming probability it simply coalesced gradually out of random motions. Just because you see what looks like a photograph, there’s no reason to believe it was preceded by an actual event that the photo purports to represent. If the random motions of the atoms create a person with firm memories of the past, all of those memories are overwhelmingly likely to be false.
This thought experiment was originally relevant because Boltzmann himself (and before him Lucretius, Hume, etc.) suggested that our world might be exactly this: a big box of gas, evolving for all eternity, out of which our current low-entropy state emerged as a random fluctuation. As was pointed out by Eddington, Feynman, and others, this idea doesn’t work, for the reasons just stated; given any one bit of universe that you might want to make (a person, a solar system, a galaxy, and exact duplicate of your current self), the rest of the world should still be in a maximum-entropy state, and it clearly is not. This is called the “Boltzmann Brain problem,” because one way of thinking about it is that the vast majority of intelligent observers in the universe should be disembodied brains that have randomly fluctuated out of the surrounding chaos, rather than evolving conventionally from a low-entropy past. That’s not really the point, though; the real problem is that such a fluctuation scenario is cognitively unstable — you can’t simultaneously believe it’s true, and have good reason for believing its true, because it predicts that all the “reasons” you think are so good have just randomly fluctuated into your head!
All of which would seemingly be little more than fodder for scholars of intellectual history, now that we know the universe is not an eternal box of gas. The observable universe, anyway, started a mere 13.8 billion years ago, in a very low-entropy Big Bang. That sounds like a long time, but the time required for random fluctuations to make anything interesting is enormously larger than that. (To make something highly ordered out of something with entropy S, you have to wait for a time of order eS. Since macroscopic objects have more than 1023 particles, S is at least that large. So we’re talking very long times indeed, so long that it doesn’t matter whether you’re measuring in microseconds or billions of years.) Besides, the universe is not a box of gas; it’s expanding and emptying out, right?
Ah, but things are a bit more complicated than that. We now know that the universe is not only expanding, but also accelerating. The simplest explanation for that — not the only one, of course — is that empty space is suffused with a fixed amount of vacuum energy, a.k.a. the cosmological constant. Vacuum energy doesn’t dilute away as the universe expands; there’s nothing in principle from stopping it from lasting forever. So even if the universe is finite in age now, there’s nothing to stop it from lasting indefinitely into the future.
But, you’re thinking, doesn’t the universe get emptier and emptier as it expands, leaving no particles to fluctuate? Only up to a point. A universe with vacuum energy accelerates forever, and as a result we are surrounded by a cosmological horizon — objects that are sufficiently far away can never get to us or even send signals, as the space in between expands too quickly. And, as Stephen Hawking and Gary Gibbons pointed out in the 1970’s, such a cosmology is similar to a black hole: there will be radiation associated with that horizon, with a constant temperature.
In other words, a universe with a cosmological constant is like a box of gas (the size of the horizon) which lasts forever with a fixed temperature. Which means there are random fluctuations. If we wait long enough, some region of the universe will fluctuate into absolutely any configuration of matter compatible with the local laws of physics. Atoms, viruses, people, dragons, what have you. The room you are in right now (or the atmosphere, if you’re outside) will be reconstructed, down to the slightest detail, an infinite number of times in the future. In the overwhelming majority of times that your local environment does get created, the rest of the universe will look like a high-entropy equilibrium state (in this case, empty space with a tiny temperature). All of those copies of you will think they have reliable memories of the past and an accurate picture of what the external world looks like — but they would be wrong. And you could be one of them.
That would be bad.
Discussions of the Boltzmann Brain problem typically occur in the context of speculative ideas like eternal inflation and the multiverse. (Not that there’s anything wrong with that.) And, let’s admit it, the very idea of orderly configurations of matter spontaneously fluctuating out of chaos sounds a bit loopy, as critics have noted. But everything I’ve just said is based on physics we think we understand: quantum field theory, general relativity, and the cosmological constant. This is the real world, baby. Of course it’s possible that we are making some subtle mistake about how quantum field theory works, but that is more speculative than taking the straightforward prediction seriously.
Modern cosmologists have a favorite default theory of the universe, labeled ΛCDM, where “Λ” stands for the cosmological constant and “CDM” for Cold Dark Matter. What we’re pointing out is that ΛCDM, the current leading candidate for an accurate description of the cosmos, can’t be right all by itself. It has a Boltzmann Brain problem, and is therefore cognitively unstable, and unacceptable as a physical theory.
Can we escape this unsettling conclusion? Sure, by tweaking the physics a little bit. The simplest route is to make the vacuum energy not really a constant, e.g. by imagining that it is a dynamical field (quintessence). But that has it’s own problems, associated with very tiny fine-tuned parameters. A more robust scenario would be to invoke quantum vacuum decay. Maybe the vacuum energy is temporarily constant, but there is another vacuum state out there in field space with an even lower energy, to which we can someday make a transition. What would happen is that tiny bubbles of the lower-energy configuration would appear via quantum tunneling; these would rapidly grow at the speed of light. If the energy of the other vacuum state were zero or negative, we wouldn’t have this pesky Boltzmann Brain problem to deal with.
Fine, but it seems to invoke some speculative physics, in the form of new fields and a new quantum vacuum state. Is there any way to save ΛCDM without invoking new physics at all?
The answer is — maybe! This is where Kim and I come in, although some of the individual pieces of our puzzle were previously put together by other authors. The first piece is a fun bit of physics that hit the news media earlier this year: the possibility that the Higgs field can itself support another vacuum state other than the one we live in. (The reason why this is true is a bit subtle, but it comes down to renormalization group effects.) That’s right: without introducing any new physics at all, it’s possible that the Higgs field will decay via bubble nucleation some time in the future, dramatically changing the physics of our universe. The whole reason the Higgs is interesting is that it has a nonzero value even in empty space; what we’re saying here is that there might be an even larger value with an even lower energy. We’re not there now, but we could get there via a phase transition. And that, Kim and I point out, has a possibility of saving us from the Boltzmann Brain problem.
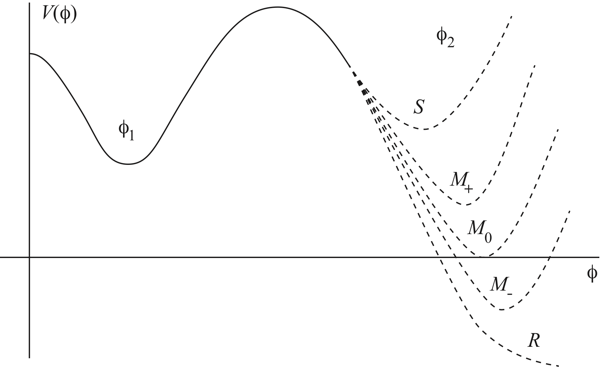
Imagine that the plot of “energy of empty space” versus “value of the Higgs field” looks like this.
φ is the value of the Higgs field. Our current location is φ1, where there is some positive energy. Somewhere out at a much larger value φ2, with a different energy. If the energy at φ2 is greater than at φ1, our current vacuum is stable. If it’s any lower value, we are “metastable”; our current situation can last for a while, but eventually we will transition to a different state. Or the Higgs can have no other vacuum far away, a “runaway” solution. (Note that if the energy in the other state is negative, space inside the bubbles of new vacuum will actually collapse to a Big Crunch rather than expanding.)
But even if that’s true, it’s not good enough by itself. Imagine that there is another vacuum state, and that we can nucleate bubbles that create regions of that new phase. The bubbles will expand at nearly the speed of light — but will they ever bump into other bubbles, and complete the transition from our current phase to the new one? Will the transition “percolate,” in other words? The answer is only “yes” if the bubbles are created rapidly enough. If they are created too slowly, the cosmological horizons come into play — spacetime expands so fast that two random bubbles will never meet each other, and the volume of space left in the original phase (the one we’re in now) keeps growing without bound. (This is the “graceful exit problem” of Alan Guth’s original inflationary-universe scenario.)
So given that the Higgs field might support a different quantum vacuum, we have two questions. First, is our current vacuum stable, or is there actually a lower-energy vacuum to which we can transition? Second, if there is a lower-energy vacuum, does our vacuum decay fast enough that the transition percolates, or do we get stuck with an ever-increasing amount of space in the current phase?
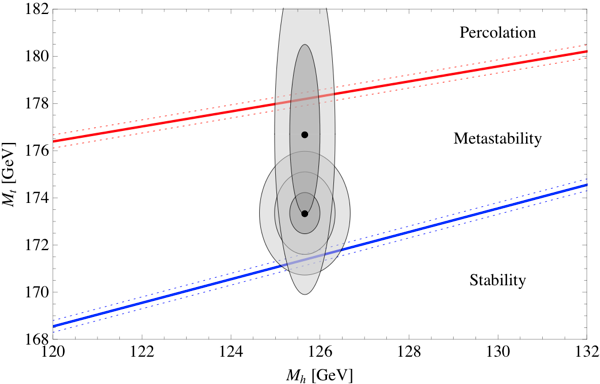
The answers depend on the precise value of the parameters that specify the Standard Model of particle physics, and therefore determine the renormalized Higgs potential. In particular, two parameters turn out to be the most important: the mass of the Higgs itself, and the mass of the top quark. We’ve measured both, but of course our measurements only have a certain precision. Happily, the answers to the two questions we are asking (is our vacuum stable, and does it decay quickly enough to percolate) have already been calculated by other groups: the stability question has been tackled (most recently, after much earlier work) by Buttazzo et al., and the percolation question has been tackled by Arkani-Hamed et al. Here are the answers, plotted in the parameter space defined by the Higgs mass and the top mass. (Dotted lines represent uncertainties in another parameter, the QCD coupling constant.)
We are interested in the two diagonal lines. If you are below the bottom line, the Higgs field is stable, and you definitely have a Boltzmann Brain problem. If you are in between the two lines, bubbles nucleate and grow, but they don’t percolate, and our current state survives. (Whether or not there is a Boltzmann-Brain problem is then measure-dependent, see below.) If you are above the top line, bubbles nucleate quite quickly, and the transition percolates just fine. However, in that region the bubbles actually nucleate too fast; the phase transition should have already happened! The favored part of this diagram is actually the top diagonal line itself; that’s the only region in which we can definitely avoid Boltzmann Brains, but can still be here to have this conversation.
We’ve also plotted two sets of ellipses, corresponding to the measured values of the Higgs and top masses. The most recent LHC numbers put the Higgs mass at 125.66 ± 0.34 GeV, which is quite good precision. The most recent consensus number for the top quark mass is 173.20 ± 0.87 GeV. Combining these results gives the lower of our two sets of ellipses, where we have plotted one-sigma, two-sigma, and three-sigma contours. We see that the central value is in the “metastable” regime, where there can be bubble nucleation but the phase transition is not fast enough to percolate. The error bars do extend into the stable region, however.
Interestingly, there has been a bit of controversy over whether this measured value of the top quark mass is the same as the parameter we use in calculating the potential energy of the Higgs field (the so-called “pole” mass). This is a discussion that is a bit outside my expertise, but a very recent paper by the CMS collaboration tries to measure the number we actually want, and comes up with much looser error bars: 176.7 ± 3.6 GeV. That’s where we got our other set of ellipses (one-sigma and two-sigma) from. If we take these numbers at face value, it’s possible that the top quark could be up there at 178 GeV, which would be enough to live on the viability line, where the phase transition will happen quickly but not too quickly. My bet would be that the consensus numbers are close to correct, but let’s put it this way: we are predicting that either the pole mass of the top quark turns out to be 178 GeV, or there is some new physics that kicks in to destabilize our current vacuum.
I was a bit unclear about what happens in the vast “metastable” region between stability and percolation. That’s because the situation is actually a bit unclear. Naively, in that region the volume of space in our current vacuum grows without bound, and Boltzmann Brains will definitely dominate. But a similar situation arises in eternal inflation, leading to what’s called the cosmological measure problem. The meat of our paper was not actually plotting a couple of curves that other people had calculated, but attempting to apply approaches to the eternal-inflation measure problem to our real-world situation. The results were a bit inconclusive. In most measures, it’s safe to say, the Boltzmann Brain problem is as bad as you might have feared. But there is at least one — a modified causal-patch measure with terminal vacua, if you must know — in which the problem is avoided. I’m not sure if there is some principled reason to believe in this measure other than “it gives an acceptable answer,” but our results suggest that understanding cosmological measure theory may be important even if you don’t believe in eternal inflation.
A final provocative observation that I’ve been saving for last. The safest place to be is on the top diagonal line in our diagram, where we have bubbles nucleating fast enough to percolate but not so fast that they should have already happened. So what does it mean, “fast enough to percolate,” anyway? Well, roughly, it means you should be making new bubbles approximately once per current lifetime of our universe. (Don Page has done a slightly more precise estimate of 20 billion years.) On the one hand, that’s quite a few billion years; it’s not like we should rush out and buy life insurance. On the other hand, it’s not that long. It means that roughly half of the lifetime of our current universe has already happened. And the transition could happen much faster — it could be tomorrow or next year, although the chances are quite tiny.
For our purposes, avoiding Boltzmann Brains, we want the transition to happen quickly. Amusingly, most of the existing particle-physics literature on decay of the Higgs field seems to take the attitude that we should want it to be completely stable — otherwise the decay of the Higgs will destroy the universe! It’s true, but we’re pointing out that this is a feature, not a bug, as we need to destroy the universe (or at least the state its currently in) to save ourselves from the invasion of the Boltzmann Brains.
All of this, of course, assumes there is no new physics at higher energies that would alter our calculations, which seems an unlikely assumption. So the alternatives are: new physics, an improved understanding of the cosmological measure problem, or a prediction that the top quark is really 178 GeV. A no-lose scenario, really.
Richard, random fluctuations are not the only way in which conscious entities can arise, they can also reproduce and reproduction is vastly more likely to produce them. So if your F1 is large enough to sustain reproduction while F2 isn’t F1 will easily win.
Greg Egan– It’s a reasonable question. Generally it’s very hard to prove ergodic theorems, because there are cases when evolution is clearly not ergodic. However, typically those cases boil down to the fact that there is some hidden conservation law, which confines the evolution to a subset of phase space. You wouldn’t expect something like that here. More importantly, you’re looking at one horizon-volume sized region at a time, which really isn’t a closed system (things can exit the horizon). When you have a perturbed system, it’s much more reasonable to think the behavior is approximately ergodic, but again hard to prove.
AI, it’s still capped by a linear function of the size of the F1 universe (it may increase exponentially for a period within F1, but that won’t be sustainable). Assuming the multiverse is at least temporally infinite, exponential will always beat linear in the long run (and we are talking about the long run).
I’m not sure that I understand how Boltzmann brains can exist at all, at least in the Many Worlds interpretation (they would seem to be a problem for the Copenhagen interpretation, and I know far too little about other interpretations to be able to say anything even remotely cogent about them). Boltzmann brains are often represented (and I don’t know how valid this representation is, I may be being misled by a pop sci understanding, here) as being a small “downward” fluctuation from a higher entropy state that is immensely smaller than a normal, universe-creating downward fluctuation. For the fluctuation responsible for creating the brain to be small, though, it must have a lowest possible entropy, a bottom to the well, beyond which there is no lower entropy state. In Many Worlds, I don’t really see how that’s possible. A cluster of particles arranged into a thinking brain will have multiple different ways it can evolve. The vast majority of these will involve an increase in its entropy (by definition), and it is these that it will experience as its future. Unless the particles/waves/what have you comprising the brain are at their lowest possible entropic configuration, though–and given that they’re capable of thinking, that seems very unlikely–they will also possess a very small subset of ways in which they can evolve that result in a net decrease in entropy. This subset of possibilities will, from their point of view, be their past, and in Many Worlds, as I understand it, all those possibilities ought to be explored. Then, well, it’s just a matter of rinsing and repeating.
Now, I have no way of knowing whether this basic approach would work for a universe with different laws of physics than our own. But in our universe, the laws of physics appear to be such that it is possible for matter to reach immensely low levels of entropy, because that’s precisely what we observe to have happened, with the early universe being incredibly low entropy relative to our own. If my understanding of Many Worlds is correct, then, and all possibilities are explored, any given Boltzmann brain–even if, from our point of view, it materialized out of nothingness–will from its perspective be the product of normal evolution from lower entropy conditions, which will themselves (from their point of view) have an even lower-entropy past. Those lower entropy states are immensely improbable, of course, but that’s what makes them the past and not the future. If we think of the universe as a whole as having one single arrow of time that always goes in the same direction, Boltzmann brains are a problem. If we realize that a brain that materializes out of nothingness will, from its perspective, be moving in the “opposite” direction through time that we are–and that once it reaches an entropy minimum, it has reached the lowest possible level of entropy that its constituent energies can assume–then the problem would seem to vanish.
…Now, again, all of this is built on an immensely shaky foundation, and I probably have no clue what I’m talking about. My hope, at least, is that if I’m wrong I’m wrong in an interesting way.
If the monkeys’ typing is perfectly random, they will never type Hamlet or any other great work of literature. The sequence of letters in english (or other language) is not uniformly random. For the monkeys to type anything meaningful, their typing would have to significantly deviate from uniform randomnicity (is that a word?)
Really, it’s like saying that an analog white noise generator, if run for a long enough time, will produce a perfect sine wave…
The universe has already produced a Hamlet through the consciousness of Shakespeare. It is something that happened in the past, impossible to repeat.
However physics saved it, for physics produces the paper and the ink and the printing presses to reproduce Hamlet in the physical. And therein lies the difference; physics remoulds the past, and philosophy deals with what is to come. A philosopher will look upon the heavens in awe tomorrow night and ponder “All of that comes to me in the blink of an eye”, but physics will analyse that what he will see is 13.7 billions light years old.
Well, the physics is interesting.
However I take a very dim view to predictions out of current physics that aren’t yet tested. It is arguably somewhat akin to “new physics” in that it can fail to be a fact. There is a related reason why we for example test the universal speed limit again and again, improving its value and rejecting cases where the proposal it didn’t work didn’t work.
So to me there is no difference to “invoke new physics or a particular cosmological measure”. And I don’t think the idea of BBs is influencing whether or not ΛCDM is an empirical success. It is a success in practice, according to WMAP and now Planck. I hear that cosmologists, for reasons that are unclear to me, want to see primordial gravity waves in order to consider the observation “home free”. But maybe a lack of such observation will result in more than a grudging acceptance, we will have to wait and see.
On the contrary, I think Planck has made eternal inflation go from being a speculation to a main alternative unless I am mistaken. The inflation potential was concave after all, and by precisely the same arguments raised in the post it is (AFAIK) a straight prediction out of quantum effects on the inflaton potential.
As a layman I would actually consider it, as well as its multiverses, tested and in better shape if Weinberg’s measure-less prediction of the cosmological constant is considered valid. This work, if it is successful, would seem to join the same type of test considering it could also be done from assuming eternal inflation (with BBs).
Also, I don’t see how appeal to philosophic untestable ideas are useful (“cognitively unstable”). Cf what “Boltzmann’s Brain” and Greg Egan notes on this.
Interesting that assuming BBs predicts a finite lifetime. IIRC Bousso et al predicts the same from the causal-patch measure, but a lot less remaining half life of some 5 Gy or so.
Bousso: http://arxiv.org/abs/1009.4698 . “The phenomenon that time can end is universal to all geometric cutoff s. But the rate at which this is likely to happen, per unit proper time along the observer’s worldline, is cutoff -specific.”
The causal-patch measure gives an expectation of ~ 5.3 Gy, but a “half life” (50 % likelihood) for less than 3.7 Gy. [p7]
Evidently this is without BBs, just from having observers.
Interesting discussion, whenever infinities occur in physics we know we have a problem. Yet here we are casually using the term infinity to make some, apparently, deep points re the universe. Angels points of needles?
Pingback: Carroll: “either the pole mass of the top quark turns out to be 178 GeV, or there is some new physics that kicks in to destabilize our current vacuum.” | Gordon's shares
I want to comment on the resolution mentioned in Wikipedia.
It’s deeply flawed because it fails to appreciate the stupendous amount of order that we observe around us. I find it ridiculous to say that the whole of the highly ordered observable universe is necessary just for the process of natural selection on Earth.
And the same goes for any anthropic-principle-based argument.
The best resolution to the paradox was mentioned in Eric Winsberg’s “Bumps on the Road to Here (from Eternity)”, and reproduced in AI’s 4th point. It’s vastly cheaper, and hence vastly more likely, for the universe to produce BBs with fake memories and sense perceptions that produce the “observations” we make.
The resolution’s only flaw is that we expect the universe to give a hoot about our epistemological prejudices.
The fine structure constant α=e²/4πεₒħc is thought to vary across space and over time, see Webb et al, and with gravitational potential, see this. Also see Milgrom’s page 5 for mention of “modifying the ‘elasticity’ of spacetime (except perhaps its strength), as is done in f [R] theories and the like”. And remember that “the energy of the gravitational field shall act gravitatively in the same way as any other form of energy”.
So a gravitational field is a place where spatial energy-density varies, and “the strength of space” varies too. Since Ʌ is the “energy density in otherwise empty space” ΛCDM isn’t quite right because it ought to be a variable-Λ model. Get a stress-ball and squeeze it down in your fist, then let go. Then get some silly putty, stretch it out, then watch it droop faster and faster. As space expands the strength reduces along with the energy density, so it expands faster. So the universe is like a box of gas which gets bigger and bigger, so the atoms stop meeting. Bye-bye Boltzmann brains. Like the multiverse they’re built on a fine-tuned canard. Sean I’m surprised you’re even going near such junk.
I don’t see how a vacuum state does anything to solve the Boltzmann brain problem. After all, just like how our can by chance create a small bubble of the new vacuum, shouldn’t this new vacuum occasionally create bubbles of the old vacuum. And can’t those bubbles be arbitrary large, even though larger bubbles are progressively less likely. And given enough time, wouldn’t these bubbles spontaneously form with any possible form of old matter, including a Boltzmann brain?
Hi,
doesn’t the cosmic horizon itself expand with the speed of light? in which case the “box” is still infinitely big, so that the Boltzmann brain problem wouldn’t really apply to the universe…
I’m probably wrong, but it would be nice to get some feedback,
thanks
Pingback: Paperback Day! | Sean Carroll
Jess– In a universe with nothing but vacuum energy (called de Sitter space), the horizon is a fixed distance away. Particles move out beyond it, but the horizon stays put.
I don’t think that’s right Sean. Or the way it’s described as “a positive (repulsive) cosmological constant Ʌ (corresponding to a positive vacuum energy density and negative pressure)”. The dimensionality of energy is pressure x volume. Space has a positive energy density and a positive volume. It has to be a positive pressure, like the stress-ball. IMHO people only think it’s a negative pressure because they think of gravity as being positive energy and attractive. But it’s the gradient in energy density that results in gravity, not the energy density itself. If the whole universe has the same energy density, there is no gravity. We surely know that, because here we are. The universe didn’t collapse when it was small and dense.
Pingback: El campo de Higgs, el inflatón, la energía oscura y los monopolos magnéticos | Francis (th)E mule Science's News
Pingback: Fine-Tuning on the TV: A Review of ABC’s Catalyst | Letters to Nature
In what way does lambdaCDM have
a Boltzmann Brain problem? The current age of the universe (4E20) seconds is way too small for macroscopic Boltzmann Brains to have
formed. In addition, wouldn’t the brain
formation rate fall as the temperature drops? Even if the universe eventually lasts long enough for Boltzmann Brains to proliferate, that does not make the universe cognitively unstable at the current epoch. So, I don’t understand why this is a problem for LambdaCDM.
Please enlighten me.
Thanks,
A concerned denizen of the universe
Hi,
Could the universe eventually reach infinite entropy after an infinite time?
With everything in perfect equilibrium…there wouldn’t be any fluctuations to cause the Brain problem. Quantum fluctuations should smooth out very quickly (compared to the time it takes to create a Brain).
Would appreciate any thoughts on this!
Sean, you’ve made an implicit assumption of a uniform xerographic distribution. The BB problem, and the problem of cognitive instability, is resolved by instead assuming a nonuniform xerographic distribution: http://arxiv.org/abs/1004.3816
Or, in less fancy language: just make the “working assumption” that we’re not Boltzmann brains, and then do whatever we can to test this assumption. So far, it passes every test!
This is called the “Boltzmann Brain problem,” because one way of thinking about it is that the vast majority of intelligent observers in the universe should be disembodied brains that have randomly fluctuated out of the surrounding chaos, rather than evolving conventionally from a low-entropy past.
A simple question. Since I bought one of Sean’s books last month in Manchester (Tony Readhead is my witness), maybe he can answer it directly: How do you know that the vast majority of intelligent observers in the universe evolved conventionally from a low-entropy past? What evidence do you have? In particular, how do you know that this evidence is not a false memory?
How can you prove that you are not a Boltzmann brain?
More generally, can you prove that you are not dreaming? I have vivid dreams which, while they last, are just as real to me as (what I assume is) my non-dreaming state. In particular, the same laws of physics apply. Just last night I had such a dream, which included asking myself if I were dreaming and concluding that I wasn’t. 😐
On a similar note, is “prove you are not a Boltzmann brain” essentially the same as “prove you are not being simulated”?
In both the Boltzmann-brain case and the simulation case, once you admit the possibility, you can’t say anything about its probability based on your observations, since in the former case they are based on false memories, not on the real universe, and in the latter case they are based on the simulated physics, not the physics of the universe containing the simulation.
Mark– We make that assumption quite explicitly, because it’s the right assumption to make! Clearly I will have to put the arguments in the form of a paper.
Philip– You can’t prove that you’re not a BB, just like you can’t prove that you’re not dreaming, or being fed false information by a whimsical demon. Nor can you make any progress on understanding the world in reliable ways if any of those scenarios is true. Therefore, we work to develop models in which they are not true.