This year we give thanks for a technique that is central to both physics and mathematics: the Fourier transform. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, and Landauer’s Principle.)
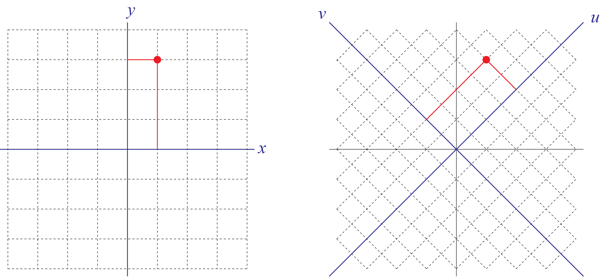
Let’s say you want to locate a point in space — for simplicity, on a two-dimensional plane. You could choose a coordinate system (x, y), and then specify the values of those coordinates to pick out your point: (x, y) = (1, 3).
But someone else might want to locate the same point, but they want to use a different coordinate system. That’s fine; points are real, but coordinate systems are just convenient fictions. So your friend uses coordinates (u, v) instead of (x, y). Fortunately, you know the relationship between the two systems: in this case, it’s u = y+x, v = y-x. The new coordinates are rotated (and scaled) with respect to the old ones, and now the point is represented as (u, v) = (4, 2).
Fourier transforms are just a fancy version of changes of coordinates. The difference is that, instead of coordinates on a two-dimensional space, we’re talking about coordinates on an infinite-dimensional space: the space of all functions. (And for technical reasons, Fourier transforms naturally live in the world of complex functions, where the value of the function at any point is a complex number.)
Think of it this way. To specify some function f(x), we give the value of the function f for every value of the variable x. In principle, an infinite number of numbers. But deep down, it’s not that different from giving the location of our point in the plane, which was just two numbers. We can certainly imagine taking the information contained in f(x) and expressing it in a different way, by “rotating the axes.”
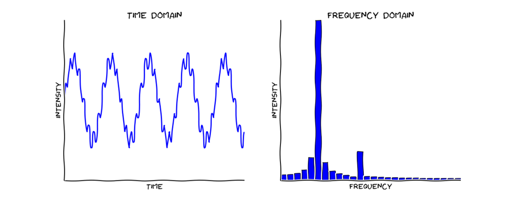
That’s what a Fourier transform is. It’s a way of specifying a function that, instead of telling you the value of the function at each point, tells you the amount of variation at each wavelength. Just as we have a formula for switching between (u, v) and (x, y), there are formulas for switching between a function f(x) and its Fourier transform f(ω):
.
Absorbing those formulas isn’t necessary to get the basic idea. If the function itself looks like a sine wave, it has a specific wavelength, and the Fourier transform is just a delta function (infinity at that particular wavelength, zero everywhere else). If the function is periodic but a bit more complicated, it might have just a few Fourier components.

In general, the Fourier transform f(ω) gives you “the amount of the original function that is periodic with period 2πω.” This is sometimes called the “frequency domain,” since there are obvious applications to signal processing, where we might want to take a signal that has an intensity that varies with time and pick out the relative strength of different frequencies. (Your eyes and ears do this automatically, when they decompose light into colors and sound into pitches. They’re just taking Fourier transforms.) Frequency, of course, is the inverse of wavelength, so it’s equally good to think of the Fourier transform as describing the “length domain.” A cosmologist who studies the large-scale distribution of galaxies will naturally take the Fourier transform of their positions to construct the power spectrum, revealing how much structure there is at different scales.
To my (biased) way of thinking, where Fourier transforms really come into their own is in quantum field theory. QFT tells us that the world is fundamentally made of waves, not particles, and it is extremely convenient to think about those waves by taking their Fourier transforms. (It is literally one of the first things one is told to do in any introduction to QFT.)
But it’s not just convenient, it’s a worldview-changing move. One way of characterizing Ken Wilson’s momentous achievement is to say “physics is organized by length scale.” Phenomena at high masses or energies are associated with short wavelengths, where our low-energy long-wavelength instruments cannot probe. (We need giant machines like the Large Hadron Collider to create high energies, because what we are really curious about are short distances.) But we can construct a perfectly good effective theory of just the wavelengths longer than a certain size — whatever size it is that our theoretical picture can describe. As physics progresses, we bring smaller and smaller length scales under the umbrella of our understanding.
Without Fourier transforms, this entire way of thinking would be inaccessible. We should be very thankful for them — as long as we use them wisely.

Note that Joseph Fourier, inventor of the transform, is not the same as Charles Fourier, utopian philosopher. Joseph, in addition to his work in math and physics, invented the idea of the greenhouse effect. Sadly that’s not something we should be thankful for right now.
Yes, we all are in debt to M. Fourier and his remarkable transform. Thanks for publishing this. Here is another formulation that I found particularly enlightening.
http://blog.revolutionanalytics.com/2014/01/the-fourier-transform-explained-in-one-sentence.html
This is the one thing I look forward to every Thanksgiving. Also pumpkin pie 🙂
Engineer Guy published a series of videos and a textbook explaining how Albert Michaelson’s Harmonic Analyzer machine works. It is a great way to visualize and understand how Fourier Transforms works without any math knowledge. https://www.youtube.com/watch?v=NAsM30MAHLg&index=1&list=PL0INsTTU1k2UYO9Mck-i5HNqGNW5AeEwq
Sean,
It appears that there is a “pi” missing under the square roots of the transform equations.
Best, 🙂
Marko
I wonder why the wavelet transform never really caught on in physics, as a middle road between coordinate and momentum representations.
There was indeed a missing π. No more.
We need Fourier transforms in all sorts of signal processing applications. There would be no autotune without them. Wavelet transforms hold a lot of promise as well.
It’s cool how a problem is opaque in one coordinate system and transparent in another. How entirely new techniques are enabled by new coordinate systems.
you wouldn’t be able to show these pictures without the mighty Fourrier Transform either (with small file size at least), jpg compression is almost entirely based around it 🙂
in QED feynman said that every feature of existence is a particle and a probabilistic behaviour controls its future, even light. Now you say the opposite in field theory. Can you clarify this if you please Sir?
Now can you explain what’s going on in a Laplace transform?
Thank you Dr. C.
To be sure there is much to be thankful for. For me your insights into mathematics is a wonder and I am thankful for it and your sharing.
However without the chemistry of greenhouse gases we would be a frozen ball with no plants or animals but perhaps only anaerobic bacteria.
.
Matt,
It’s been a long time, but I’ll give it a whirl. The LT is closely related to the FT as is seen in the mathematical forms. They are slightly different ‘coordinate systems’ that solve problems more easily depending on the constraints and symmetries. The LT is ideal for analyzing causal dynamical systems (dynamic systems that only respond after excited, so the response function is zero for all time prior to the excitation). That’s why the original LT integrates from t=0 to infinity. These systems are usually described by differential equations that transform into simple polynomials, greatly simplifying their solutions.
OK, thanks! It seems to me, it is the basics for understanding the ‘dual nature’ of elementary particles.
I think one day it will turn out that Walsh function and related concepts are going to be much more powerful in describing physics, Maybe even TOE.
http://en.wikipedia.org/wiki/Walsh_function
My favorite forward and backward Fourier transform devices are the piano and the human ear.
.
Also, if the Fourier transform is just a change of coordinates, and “coordinate systems are just convenient fictions”, how can QFT tells us that the world is fundamentally made of waves, not particles? Aren’t both convenient fictions?
I share FrankL’s lack of certainty regarding QFT. If I have but little exposure to QFT, then I confess I have found even less of it to my tastes. An engineer by training, I find comfort in models that, when exposed to an error in computation, will show a clear divergence from reality. The correction of which serves to guide the humble practitioner back onto the path of the righteous. I have found these guideposts are few and far between in QFT. It seems that as soon as a nonsensical result is uncovered, a stray infinity perhaps, “best practice” calls for it to be waved away or perhaps “renormalized” by joint concurrence. Is this really a mechanism on which we can determine something like particle or wave?
@Ron Baakkonen – I don’t question the predictive ability of QFT, its just the interpretation that the world is fundamentally made of waves, not particles. It sounds like one coordinate system is being favored, which I question.
@bostontola @Claude
As an example of how transformation of coordinates can get a surprising benefit:
In the case of image compression, transforming to the frequency domain makes lossy compression easier. Human is vision less sensitive to higher frequency changes in the image, so those higher frequency components can be stored less accurately. The transformation makes it easier to figure out what part of the image is safe to “throw away” without affecting human perception of image quality.
Latverian Diplomat,
Very cool example of combining biology and math for benefit. My favorite is one of the most basic properties, conversion of convolution to multiplication. Filtering becomes almost trivial. Then you can go further with non-linear operations (logarithms) and get powerful Homomorphic processing.
Its also kinda central to modern communications systems.
I think it is odd for Sean to say the world is fundamentally made of waves. I always tell students that the resolution to wave / particle duality is that both are crude, classical physical approximations and linguistic analogies. We can learn how to do some nice, predictive calculations to move past the crude approximations, but we have to work very hard on our intuitions to replace the crude analogies. If you close your eyes and imagine a quantum state, it’s probably going to ‘look like’ a fuzzy wave rather than a ray in Hilbert space. But the wave is also wrong.
I remember a conversation between me and my computer science professor…
Hal: I’m trying to make a frequency vs. time graph. How would I do that with a fourier transform? Also, I’ve heard of something called a Hadamard matrix for error correction; I don’t think I understand it.”
Prof: I’m not familiar with any of that.
Dropped the class the next day and waited until the next semester to take it.
As a comp. sci. undergraduate, me and all my buddies tried to figure out how to avoid the (required) Signals and Systems course. Many of us switched to the math department. Some advisors let people substitute something else. My advisor said “They made me take it. We’re making you take it.” Pretty much the most useful course I took. Music, crystals, digital TVs, pretty much everything depends on some sort of time/frequency duality.
Speaking of digital TVs, back when both HDTV and satellite broadcasting were still being dreamed about, Japan (NHK) devised a satellite broadcasting system that was all analog. It required a ton of power and they only got 3 channels. A few years later, a couple of commercial companies were broadcasting 300 channels using less power. “Why didn’t you just do digital from the start?” “We thought the semiconductor industry wouldn’t be able to bring the cost of the computation required to decode digital broadcasts to consumer levels.” One of the worst technology predictions in human history, brought to you by the difficulty of the FFT and a failure to have faith in Saint Moore.