Search Results for: Thanksgiving

 This year we give thanks for a feature of nature that is frequently misunderstood: quanta. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, the Fourier Transform, Riemannian Geometry, the speed of light, the Jarzynski equality, the moons of Jupiter, space, black hole entropy, electromagnetism, and Arrow’s Impossibility Theorem.)

Of course quantum mechanics is very important and somewhat misunderstood in its own right; I can recommend a good book if you’d like to learn more. But we’re not getting into the measurement problem or the reality problem just now. I want to highlight one particular feature of quantum mechanics that is sometimes misinterpreted: the fact that some things, like individual excitations of quantized fields (“particles”) or the energy levels of atoms, come in sets of discrete numbers, rather than taking values on a smooth continuum. These discrete chunks of something-or-other are the “quanta” being referred to in the title of a different book, scheduled to come out next spring.

The basic issue is that people hear the phrase “quantum mechanics,” or even take a course in it, and come away with the impression that reality is somehow pixelized — made up of smallest possible units — rather than being ultimately smooth and continuous. That’s not right! Quantum theory, as far as it is currently understood, is all about smoothness. The lumpiness of “quanta” is just apparent, although it’s a very important appearance.

What’s actually happening is a combination of (1) fundamentally smooth functions, (2) differential equations, (3) boundary conditions, and (4) what we care about.

This might sound confusing, so let’s fix ideas by looking at a ubiquitous example: the simple harmonic oscillator. That can be thought of as a particle moving in one dimension, x, with a potential energy that looks like a parabola: . In classical mechanics, there is a lowest-energy state where the particle just sits at the bottom of its potential, unmoving, so both its kinetic and potential energies are zero. We can give it any positive amount of energy we like, either by kicking it to impart motion or just picking it up and dropping it in the potential at some point other than the origin.

Quantum mechanically, that’s not quite true (although it’s truer than you might think). Now we have a set of discrete energy levels, starting from the ground state and going upward in equal increments. Quanta!

But we didn’t put the quanta in. They come out of the above four ingredients. First, the particle is described not by its position and momentum, but by its wave function, . Nothing discrete about that; it’s a fundamentally smooth function. But second, that function isn’t arbitrary; it’s going to obey the Schrödinger equation, which is a special differential equation. The Schrödinger equation tells us how the wave function evolves with time, and we can solve it starting with any initial wave function we like. Still nothing discrete there. But there is one requirement, coming from the idea of boundary conditions: if the wave function grows (or remains constant) as , the potential energy grows along with it. (It actually has to diminish at infinity just to be a wave function at all, but for the moment let’s think about the energy.) When we bring in the fourth ingredient, “what we care about,” the answer is that we care about low-energy states of the oscillator. That’s because in real-world situations, there is dissipation. Whatever physical system is being modeled by the harmonic oscillator, in reality it will most likely have friction or be able to give off photons or something like that. So no matter where we start, left to its own devices the oscillator will diminish in energy. So we generally care about states with relatively low energy.

Since this is quantum mechanics after all, most states of the wave function won’t have a definite energy, in much the same way they will not have a definite position or momentum. (They have “an energy” — the expectation value of the Hamiltonian — but not a “definite” one, since you won’t necessarily observe that value.) But there are some special states, the energy eigenstates, associated with a specific, measurable amount of energy. It is those states that are discrete: they come in a set made of a lowest-energy “ground” state, plus a ladder of evenly-spaced states of ever-higher energy.

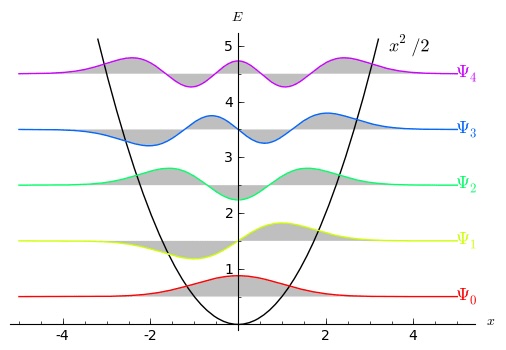
We can even see why that’s true, and why the states look the way they do, just by thinking about boundary conditions. Since each state has finite energy, the wave function has to be zero at the far left and also at the far right. The energy in the state comes from two sources: the potential, and the “gradient” energy from the wiggles in the wave function. The lowest-energy state will be a compromise between “staying as close to as possible” and “not changing too rapidly at any point.” That compromise looks like the bottom (red) curve in the figure: starts at zero on the left, gradually increases and then decreases as it continues on to the right. It is a feature of eigenstates that they are all “orthogonal” to each other — there is zero net overlap between them. (Technically, if you multiply them together and integrate over , the answer is zero.) So the next eigenstate will first oscillate down, then up, then back to zero. Subsequent energy eigenstates will each oscillate just a bit more, so they contain the least possible energy while being orthogonal to all the lower-lying states. Those requirements mean that they will each pass through zero exactly one more time than the state just below them.

And that is where the “quantum” nature of quantum mechanics comes from. Not from fundamental discreteness or anything like that; just from the properties of the set of solutions to a perfectly smooth differential equation. It’s precisely the same as why you get a fundamental note from a violin string tied at both ends, as well as a series of discrete harmonics, even though the string itself is perfectly smooth.

One cool aspect of this is that it also explains why quantum fields look like particles. A field is essentially the opposite of a particle: the latter has a specific location, while the former is spread all throughout space. But quantum fields solve equations with boundary conditions, and we care about the solutions. It turns out (see above-advertised book for details!) that if you look carefully at just a single “mode” of a field — a plane-wave vibration with specified wavelength — its wave function behaves much like that of a simple harmonic oscillator. That is, there is a ground state, a first excited state, a second excited state, and so on. Through a bit of investigation, we can verify that these states look and act like a state with zero particles, one particle, two particles, and so on. That’s where particles come from.

We see particles in the world, not because it is fundamentally lumpy, but because it is fundamentally smooth, while obeying equations with certain boundary conditions. It’s always tempting to take what we see to be the underlying truth of nature, but quantum mechanics warns us not to give in.

Is reality fundamentally discrete? Nobody knows. Quantum mechanics is certainly not, even if you have quantum gravity. Nothing we know about gravity implies that “spacetime is discrete at the Planck scale.” (That may be true, but it is not implied by anything we currently know; indeed, it is counter-indicated by things like the holographic principle.) You can think of the Planck length as the scale at which the classical approximation to spacetime is likely to break down, but that’s a statement about our approximation schemes, not the fundamental nature of reality.

States in quantum theory are described by rays in Hilbert space, which is a vector space, and vector spaces are completely smooth. You can construct a candidate vector space by starting with some discrete things like bits, then considering linear combinations, as happens in quantum computing (qubits) or various discretized models of spacetime. The resulting Hilbert space is finite-dimensional, but is still itself very much smooth, not discrete. (Rough guide: “quantizing” a discrete system gets you a finite-dimensional Hilbert space, quantizing a smooth system gets you an infinite-dimensional Hilbert space.) True discreteness requires throwing out ordinary quantum mechanics and replacing it with something fundamentally discrete, hoping that conventional QM emerges in some limit. That’s the approach followed, for example, in models like the Wolfram Physics Project. I recently wrote a paper proposing a judicious compromise, where standard QM is modified in the mildest possible way, replacing evolution in a smooth Hilbert space with evolution on a discrete lattice defined on a torus. It raises some cosmological worries, but might otherwise be phenomenologically acceptable. I don’t yet know if it has any specific experimental consequences, but we’re thinking about that.

This year we give thanks for one of the very few clues we have to the quantum nature of spacetime: black hole entropy. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, the Fourier Transform, Riemannian Geometry, the speed of light, the Jarzynski equality, the moons of Jupiter, and space.)

Black holes are regions of spacetime where, according to the rules of Einstein’s theory of general relativity, the curvature of spacetime is so dramatic that light itself cannot escape. Physical objects (those that move at or more slowly than the speed of light) can pass through the “event horizon” that defines the boundary of the black hole, but they never escape back to the outside world. Black holes are therefore black — even light cannot escape — thus the name. At least that would be the story according to classical physics, of which general relativity is a part. Adding quantum ideas to the game changes things in important ways. But we have to be a bit vague — “adding quantum ideas to the game” rather than “considering the true quantum description of the system” — because physicists don’t yet have a fully satisfactory theory that includes both quantum mechanics and gravity.

The story goes that in the early 1970’s, James Bardeen, Brandon Carter, and Stephen Hawking pointed out an analogy between the behavior of black holes and the laws of good old thermodynamics. For example, the Second Law of Thermodynamics (“Entropy never decreases in closed systems”) was analogous to Hawking’s “area theorem”: in a collection of black holes, the total area of their event horizons never decreases over time. Jacob Bekenstein, who at the time was a graduate student working under John Wheeler at Princeton, proposed to take this analogy more seriously than the original authors had in mind. He suggested that the area of a black hole’s event horizon really is its entropy, or at least proportional to it.

This annoyed Hawking, who set out to prove Bekenstein wrong. After all, if black holes have entropy then they should also have a temperature, and objects with nonzero temperatures give off blackbody radiation, but we all know that black holes are black. But he ended up actually proving Bekenstein right; black holes do have entropy, and temperature, and they even give off radiation. We now refer to the entropy of a black hole as the “Bekenstein-Hawking entropy.” (It is just a useful coincidence that the two gentlemen’s initials, “BH,” can also stand for “black hole.”)

Consider a black hole whose area of its event horizon is . Then its Bekenstein-Hawking entropy is

   

where is the speed of light, is Newton’s constant of gravitation, and is Planck’s constant of quantum mechanics. A simple formula, but already intriguing, as it seems to combine relativity (), gravity (), and quantum mechanics () into a single expression. That’s a clue that whatever is going on here, it something to do with quantum gravity. And indeed, understanding black hole entropy and its implications has been a major focus among theoretical physicists for over four decades now, including the holographic principle, black-hole complementarity, the AdS/CFT correspondence, and the many investigations of the information-loss puzzle.

But there exists a prior puzzle: what is the black hole entropy, anyway? What physical quantity does it describe?

Entropy itself was invented as part of the development of thermodynamics is the mid-19th century, as a way to quantify the transformation of energy from a potentially useful form (like fuel, or a coiled spring) into useless heat, dissipated into the environment. It was what we might call a “phenomenological” notion, defined in terms of macroscopically observable quantities like heat and temperature, without any more fundamental basis in a microscopic theory. But more fundamental definitions came soon thereafter, once people like Maxwell and Boltzmann and Gibbs started to develop statistical mechanics, and showed that the laws of thermodynamics could be derived from more basic ideas of atoms and molecules.

Hawking’s derivation of black hole entropy was in the phenomenological vein. He showed that black holes give off radiation at a certain temperature, and then used the standard thermodynamic relations between entropy, energy, and temperature to derive his entropy formula. But this leaves us without any definite idea of what the entropy actually represents.

One of the reasons why entropy is thought of as a confusing concept is because there is more than one notion that goes under the same name. To dramatically over-simplify the situation, let’s consider three different ways of relating entropy to microscopic physics, named after three famous physicists:

• Boltzmann entropy says that we take a system with many small parts, and divide all the possible states of that system into “macrostates,” so that two “microstates” are in the same macrostate if they are macroscopically indistinguishable to us. Then the entropy is just (the logarithm of) the number of microstates in whatever macrostate the system is in.
• Gibbs entropy is a measure of our lack of knowledge. We imagine that we describe the system in terms of a probability distribution of what microscopic states it might be in. High entropy is when that distribution is very spread-out, and low entropy is when it is highly peaked around some particular state.
• von Neumann entropy is a purely quantum-mechanical notion. Given some quantum system, the von Neumann entropy measures how much entanglement there is between that system and the rest of the world.

These seem like very different things, but there are formulas that relate them to each other in the appropriate circumstances. The common feature is that we imagine a system has a lot of microscopic “degrees of freedom” (jargon for “things that can happen”), which can be in one of a large number of states, but we are describing it in some kind of macroscopic coarse-grained way, rather than knowing what its exact state actually is. The Boltzmann and Gibbs entropies worry people because they seem to be subjective, requiring either some seemingly arbitrary carving of state space into macrostates, or an explicit reference to our personal state of knowledge. The von Neumann entropy is at least an objective fact about the system. You can relate it to the others by analogizing the wave function of a system to a classical microstate. Because of entanglement, a quantum subsystem generally cannot be described by a single wave function; the von Neumann entropy measures (roughly) how many different quantum must be involved to account for its entanglement with the outside world.

So which, if any, of these is the black hole entropy? To be honest, we’re not sure. Most of us think the black hole entropy is a kind of von Neumann entropy, but the details aren’t settled.

One clue we have is that the black hole entropy is proportional to the area of the event horizon. For a while this was thought of as a big, surprising thing, since for something like a box of gas, the entropy is proportional to its total volume, not the area of its boundary. But people gradually caught on that there was never any reason to think of black holes like boxes of gas. In quantum field theory, regions of space have a nonzero von Neumann entropy even in empty space, because modes of quantum fields inside the region are entangled with those outside. The good news is that this entropy is (often, approximately) proportional to the area of the region, for the simple reason that field modes near one side of the boundary are highly entangled with modes just on the other side, and not very entangled with modes far away. So maybe the black hole entropy is just like the entanglement entropy of a region of empty space?

Would that it were so easy. Two things stand in the way. First, Bekenstein noticed another important feature of black holes: not only do they have entropy, but they have the most entropy that you can fit into a region of a fixed size (the Bekenstein bound). That’s very different from the entanglement entropy of a region of empty space in quantum field theory, where it is easy to imagine increasing the entropy by creating extra entanglement between degrees of freedom deep in the interior and those far away. So we’re back to being puzzled about why the black hole entropy is proportional to the area of the event horizon, if it’s the most entropy a region can have. That’s the kind of reasoning that leads to the holographic principle, which imagines that we can think of all the degrees of freedom inside the black hole as “really” living on the boundary, rather than being uniformly distributed inside. (There is a classical manifestation of this philosophy in the membrane paradigm for black hole astrophysics.)

The second obstacle to simply interpreting black hole entropy as entanglement entropy of quantum fields is the simple fact that it’s a finite number. While the quantum-field-theory entanglement entropy is proportional to the area of the boundary of a region, the constant of proportionality is infinity, because there are an infinite number of quantum field modes. So why isn’t the entropy of a black hole equal to infinity? Maybe we should think of the black hole entropy as measuring the amount of entanglement over and above that of the vacuum (called the Casini entropy). Maybe, but then if we remember Bekenstein’s argument that black holes have the most entropy we can attribute to a region, all that infinite amount of entropy that we are ignoring is literally inaccessible to us. It might as well not be there at all. It’s that kind of reasoning that leads some of us to bite the bullet and suggest that the number of quantum degrees of freedom in spacetime is actually a finite number, rather than the infinite number that would naively be implied by conventional non-gravitational quantum field theory.

So — mysteries remain! But it’s not as if we haven’t learned anything. The very fact that black holes have entropy of some kind implies that we can think of them as collections of microscopic degrees of freedom of some sort. (In string theory, in certain special circumstances, you can even identify what those degrees of freedom are.) That’s an enormous change from the way we would think about them in classical (non-quantum) general relativity. Black holes are supposed to be completely featureless (they “have no hair,” another idea of Bekenstein’s), with nothing going on inside them once they’ve formed and settled down. Quantum mechanics is telling us otherwise. We haven’t fully absorbed the implications, but this is surely a clue about the ultimate quantum nature of spacetime itself. Such clues are hard to come by, so for that we should be thankful.

This year we give thanks for space. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, the Fourier Transform, Riemannian Geometry, the speed of light, the Jarzynski equality, and the moons of Jupiter.)

Even when we restrict to essentially scientific contexts, “space” can have a number of meanings. In a tangible sense, it can mean outer space — the final frontier, that place we could go away from the Earth, where the stars and other planets are located. In a much more abstract setting, mathematicians use “space” to mean some kind of set with additional structure, like Hilbert space or the space of all maps between two manifolds. Here we’re aiming in between, using “space” to mean the three-dimensional manifold in which physical objects are located, at least as far as our observable universe is concerned.

That last clause reminds us that there are some complications here. The three dimensions we see of space might not be all there are; extra dimensions could be hidden from us by being curled up into tiny balls (or generalizations thereof) that are too small to see, or if the known particles and forces are confined to a three-dimensional brane embedded in a larger universe. On the other side, we have intimations that quantum theories of gravity imply the holographic principle, according to which an N-dimensional universe can be thought of as arising as a projection of (N-1)-dimensions worth of information. And much less speculatively, Einstein and Minkowski taught us long ago that three-dimensional space is better thought of as part of four-dimensional spacetime.

Let’s put all of that aside. Our everyday world is accurately modeled as stuff, distributed through three-dimensional space, evolving with time. That’s something to be thankful for! But we can also wonder why it is the case.

I don’t mean “Why is space three-dimensional?”, although there is that. I mean why is there something called “space” at all? I recently gave an informal seminar on this at Columbia, and I talk about it a bit in Something Deeply Hidden, and it’s related in spirit to a question Michael Nielsen recently asked on Twitter, “Why does F=ma?”

Space is probably emergent rather than fundamental, and the ultimate answer to why it exists is probably going to involve quantum mechanics, and perhaps quantum gravity in particular. The right question is “Why does the wave function of the universe admit a description as a set of branching semi-classical worlds, each of which feature objects evolving in three-dimensional space?” We’re working on that!

But rather than answer it, for the purposes of thankfulness I just want to point out that it’s not obvious that space as we know it had to exist, even if classical mechanics had been the correct theory of the world.

Newton himself thought of space as absolute and fundamental. His ontology, as the philosophers would put it, featured objects located in space, evolving with time. Each object has a trajectory, which is its position in space at each moment of time. Quantities like “velocity” and “acceleration” are important, but they’re not fundamental — they are derived from spatial position, as the first and second derivatives with respect to time, respectively.

But that’s not the only way to do classical mechanics, and in some sense it’s not the most basic and powerful way. An alternative formulation is provided by Hamiltonian mechanics, where the fundamental variable isn’t “position,” but the combination of “position and momentum,” which together describe the phase space of a system. The state of a system at any one time is given by a point in phase space. There is a function of phase space cleverly called the Hamiltonian H(x,p), from which the dynamical equations of the system can be derived.

That might seem a little weird, and students tend to be somewhat puzzled by the underlying idea of Hamiltonian mechanics when they are first exposed to it. Momentum, we are initially taught in our physics courses, is just the mass times the velocity. So it seems like a derived quantity, not a fundamental one. How can Hamiltonian mechanics put momentum on an equal footing to position, if one is derived from the other?

The answer is that in the Hamiltonian approach, momentum is not defined to be mass times velocity. It ends up being equal to that by virtue of an equation of motion, at least if the Hamiltonian takes the right form. But in principle it’s an independent variable.

That’s a subtle distinction! Hamiltonian mechanics says that at any one moment a system is described by two quantities, its position and its momentum. No time derivatives or trajectories are involved; position and momentum are completely different things. Then there are two equations telling us how the position and the momentum change with time. The derivative of the position is the velocity, and one equation sets it equal to the momentum divided by the mass, just as in Newtonian mechanics. The other equation sets the derivative of the momentum equal to the force. Combining the two, we again find that force equals mass times acceleration (derivative of velocity).

So from the Hamiltonian perspective, positions and momenta are on a pretty equal footing. Why then, in the real world, do we seem to “live in position space”? Why don’t we live in momentum space?

As far as I know, no complete and rigorous answer to these questions has ever been given. But we do have some clues, and the basic principle is understood, even if some details remain to be ironed out.

That principle is this: we can divide the world into subsystems that interact with each other under appropriate circumstances. And those circumstances come down to “when they are nearby in space.” In other words, interactions are local in space. They are not local in momentum. Two billiard balls can bump into each other when they arrive at the same location, but nothing special happens when they have the same momentum or anything like that.

Ultimately this can be traced to the fact that the Hamiltonian of the real world is not some arbitrary function of positions and momenta; it’s a very specific kind of function. The ultimate expression of this kind of locality is field theory — space is suffused with fields, and what happens to a field at one point in space only directly depends on the other fields at precisely the same point in space, nowhere else. And that’s embedded in the Hamiltonian of the universe, in particular in the fact that the Hamiltonian can be written as an integral over three-dimensional space of a local function, called the “Hamiltonian density.”

where φ is the field (which here acts as a “coordinate”) and π is its corresponding momentum.

This represents progress on the “Why is there space?” question. The answer is “Because space is the set of variables with respect to which interactions are local.” Which raises another question, of course: why are interactions local with respect to anything? Why do the fundamental degrees of freedom of nature arrange themselves into this kind of very specific structure, rather than some other one?

We have some guesses there, too. One of my favorite recent papers is “Locality From the Spectrum,” by Jordan Cotler, Geoffrey Penington, and Daniel Ranard. By “the spectrum” they mean the set of energy eigenvalues of a quantum Hamiltonian — i.e. the possible energies that states of definite energy can have in a theory. The game they play is to divide up the Hilbert space of quantum states into subsystems, and then ask whether a certain list of energies is compatible with “local” interactions between those subsystems. The answers are that most Hamiltonians aren’t compatible with locality in any sense, and for those where locality is possible, the division into local subsystems is essentially unique. So locality might just be a consequence of certain properties of the quantum Hamiltonian that governs the universe.

Fine, but why that Hamiltonian? Who knows? This is above our pay grade right now, though it’s fun to speculate. Meanwhile, let’s be thankful that the fundamental laws of physics allow us to describe our everyday world as a collection of stuff distributed through space. If they didn’t, how would we ever find our keys?

This year we give thanks for a simple but profound principle of statistical mechanics that extends the famous Second Law of Thermodynamics: the Jarzynski Equality. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, the Fourier Transform, Riemannian Geometry, and the speed of light.)

The Second Law says that entropy increases in closed systems. But really it says that entropy usually increases; thermodynamics is the limit of statistical mechanics, and in the real world there can be rare but inevitable fluctuations around the typical behavior. The Jarzynski Equality is a way of quantifying such fluctuations, which is increasingly important in the modern world of nanoscale science and biophysics.

Our story begins, as so many thermodynamic tales tend to do, with manipulating a piston containing a certain amount of gas. The gas is of course made of a number of jiggling particles (atoms and molecules). All of those jiggling particles contain energy, and we call the total amount of that energy the internal energy U of the gas. Let’s imagine the whole thing is embedded in an environment (a “heat bath”) at temperature T. That means that the gas inside the piston starts at temperature T, and after we manipulate it a bit and let it settle down, it will relax back to T by exchanging heat with the environment as necessary.

Finally, let’s divide the internal energy into “useful energy” and “useless energy.” The useful energy, known to the cognoscenti as the (Helmholtz) free energy and denoted by F, is the amount of energy potentially available to do useful work. For example, the pressure in our piston may be quite high, and we could release it to push a lever or something. But there is also useless energy, which is just the entropy S of the system times the temperature T. That expresses the fact that once energy is in a highly-entropic form, there’s nothing useful we can do with it any more. So the total internal energy is the free energy plus the useless energy,

Our piston starts in a boring equilibrium configuration a, but we’re not going to let it just sit there. Instead, we’re going to push in the piston, decreasing the volume inside, ending up in configuration b. This squeezes the gas together, and we expect that the total amount of energy will go up. It will typically cost us energy to do this, of course, and we refer to that energy as the work W_ab we do when we push the piston from a to b.

Remember that when we’re done pushing, the system might have heated up a bit, but we let it exchange heat Q with the environment to return to the temperature T. So three things happen when we do our work on the piston: (1) the free energy of the system changes; (2) the entropy changes, and therefore the useless energy; and (3) heat is exchanged with the environment. In total we have

(There is no ΔT, because T is the temperature of the environment, which stays fixed.) The Second Law of Thermodynamics says that entropy increases (or stays constant) in closed systems. Our system isn’t closed, since it might leak heat to the environment. But really the Second Law says that the total of the last two terms on the right-hand side of this equation add up to a positive number; in other words, the increase in entropy will more than compensate for the loss of heat. (Alternatively, you can lower the entropy of a bottle of champagne by putting it in a refrigerator and letting it cool down; no laws of physics are violated.) One way of stating the Second Law for situations such as this is therefore

The work we do on the system is greater than or equal to the change in free energy from beginning to end. We can make this inequality into an equality if we act as efficiently as possible, minimizing the entropy/heat production: that’s an adiabatic process, and in practical terms amounts to moving the piston as gradually as possible, rather than giving it a sudden jolt. That’s the limit in which the process is reversible: we can get the same energy out as we put in, just by going backwards.

Awesome. But the language we’re speaking here is that of classical thermodynamics, which we all know is the limit of statistical mechanics when we have many particles. Let’s be a little more modern and open-minded, and take seriously the fact that our gas is actually a collection of particles in random motion. Because of that randomness, there will be fluctuations over and above the “typical” behavior we’ve been describing. Maybe, just by chance, all of the gas molecules happen to be moving away from our piston just as we move it, so we don’t have to do any work at all; alternatively, maybe there are more than the usual number of molecules hitting the piston, so we have to do more work than usual. The Jarzynski Equality, derived 20 years ago by Christopher Jarzynski, is a way of saying something about those fluctuations.

One simple way of taking our thermodynamic version of the Second Law (3) and making it still hold true in a world of fluctuations is simply to say that it holds true on average. To denote an average over all possible things that could be happening in our system, we write angle brackets around the quantity in question. So a more precise statement would be that the average work we do is greater than or equal to the change in free energy:

(We don’t need angle brackets around ΔF, because F is determined completely by the equilibrium properties of the initial and final states a and b; it doesn’t fluctuate.) Let me multiply both sides by -1, which means we  need to flip the inequality sign to go the other way around:

Next I will exponentiate both sides of the inequality. Note that this keeps the inequality sign going the same way, because the exponential is a monotonically increasing function; if x is less than y, we know that e^x is less than e^y.

(More typically we will see the exponents divided by kT, where k is Boltzmann’s constant, but for simplicity I’m using units where kT = 1.)

Jarzynski’s equality is the following remarkable statement: in equation (6), if we exchange  the exponential of the average work for the average of the exponential of the work , we get a precise equality, not merely an inequality:

That’s the Jarzynski Equality: the average, over many trials, of the exponential of minus the work done, is equal to the exponential of minus the free energies between the initial and final states. It’s a stronger statement than the Second Law, just because it’s an equality rather than an inequality.

In fact, we can derive the Second Law from the Jarzynski equality, using a math trick known as Jensen’s inequality. For our purposes, this says that the exponential of an average is less than the average of an exponential, . Thus we immediately get

as we had before. Then just take the log of both sides to get , which is one way of writing the Second Law.

So what does it mean? As we said, because of fluctuations, the work we needed to do on the piston will sometimes be a bit less than or a bit greater than the average, and the Second Law says that the average will be greater than the difference in free energies from beginning to end. Jarzynski’s Equality says there is a quantity, the exponential of minus the work, that averages out to be exactly the exponential of minus the free-energy difference. The function is convex and decreasing as a function of W. A fluctuation where W is lower than average, therefore, contributes a greater shift to the average of than a corresponding fluctuation where W is higher than average. To satisfy the Jarzynski Equality, we must have more fluctuations upward in W than downward in W, by a precise amount. So on average, we’ll need to do more work than the difference in free energies, as the Second Law implies.

It’s a remarkable thing, really. Much of conventional thermodynamics deals with inequalities, with equality being achieved only in adiabatic processes happening close to equilibrium. The Jarzynski Equality is fully non-equilibrium, achieving equality no matter how dramatically we push around our piston. It tells us not only about the average behavior of statistical systems, but about the full ensemble of possibilities for individual trajectories around that average.

The Jarzynski Equality has launched a mini-revolution in nonequilibrium statistical mechanics, the news of which hasn’t quite trickled to the outside world as yet. It’s one of a number of relations, collectively known as “fluctuation theorems,” which also include the Crooks Fluctuation Theorem, not to mention our own Bayesian Second Law of Thermodynamics. As our technological and experimental capabilities reach down to scales where the fluctuations become important, our theoretical toolbox has to keep pace. And that’s happening: the Jarzynski equality isn’t just imagination, it’s been experimentally tested and verified. (Of course, I remain just a poor theorist myself, so if you want to understand this image from the experimental paper, you’ll have to talk to someone who knows more about Raman spectroscopy than I do.)

This year we give thanks for a feature of the physical world that many people grumble about rather than celebrating, but is undeniably central to how Nature works at a deep level: the speed of light. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, the Fourier Transform and Riemannian Geometry.)

The speed of light in vacuum, traditionally denoted by c, is 299,792,458 meters per second. It’s exactly that, not just approximately; it turns out to be easier to measure intervals of time to very high precision than it is to measure distances in space, so we measure the length of a second experimentally, then define the meter to be “the distance that light travels 299,792,458 of in one second.” Personally I prefer to characterize c as “one light-year per year”; that’s equally exact, and it’s easier to remember all the significant figures that way.

There are a few great things about the speed of light. One is that it’s a fixed, universal constant, as measured by inertial (unaccelerating) observers, in vacuum (empty space). Of course light can slow down if it propagates through a medium, but that’s hardly surprising. The other great thing is that it’s an upper limit; physical particles, as far as we know in the real world, always move at speeds less than or equal to c.

That first fact, the universal constancy of c, is the startling feature that set Einstein on the road to figuring out relativity. It’s a crazy claim at first glance: if two people are moving relative to each other (maybe because one is in a moving car and one is standing on the sidewalk) and they measure the speed of a third object (like a plane passing overhead) relative to themselves, of course they will get different answers. But not with light. I can be zipping past you at 99% of c, directly at an oncoming light beam, and both you and I will measure it to be moving at the same speed. That’s only sensible if something is wonky about our conventional pre-relativity notions of space and time, which is what Einstein eventually figured out. It was his former teacher Minkowski who realized the real implication is that we should think of the world as a single four-dimensional spacetime; Einstein initially scoffed at the idea as typically useless mathematical puffery, but of course it turned out to be central in his eventual development of general relativity (which explains gravity by allowing spacetime to be curved).

Because the speed of light is universal, when we draw pictures of spacetime we can indicate the possible paths light can take through any point, in a way that will be agreed upon by all observers. Orienting time vertically and space horizontally, the result is the set of light cones — the pictorial way of indicating the universal speed-of-light limit on our motion through the universe. Moving slower than light means moving “upward through your light cones,” and that’s what all massive objects are constrained to do. (When you’ve really internalized the lessons of relativity, deep in your bones, you understand that spacetime diagrams should only indicate light cones, not subjective human constructs like “space” and “time.”)

The fact that the speed of light is such an insuperable barrier to the speed of travel is something that really bugs people. On everyday-life scales, c is incredibly fast; but once we start contemplating astrophysical distances, suddenly it seems maddeningly slow. It takes just over a second for light to travel from the Earth to the Moon; eight minutes to get to the Sun; over five hours to get to Pluto; four years to get to the nearest star; twenty-six thousand years to get to the galactic center; and two and a half million years to get to the Andromeda galaxy. That’s why almost all good space-opera science fiction takes the easy way out and imagines faster-than-light travel. (In the real world, we won’t ever travel faster than light, but that won’t stop us from reaching the stars; it’s much more feasible to imagine extending human lifespans by many orders of magnitude, or making cryogenic storage feasible. Not easy — but not against the laws of physics, either.)

It’s understandable, therefore, that we sometimes get excited by breathless news reports about faster-than-light signals, though they always eventually disappear. But I think we should do better than just be grumpy about the finite speed of light. Like it or not, it’s an absolutely crucial part of the nature of reality. It didn’t have to be, in the sense of all possible worlds; the Newtonian universe is a relatively sensible set of laws of physics, in which there is no speed-of-light barrier at all.

That would be a very different world indeed. …

ThanksgivingRead More »